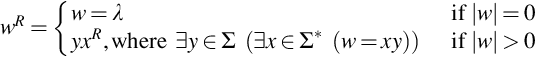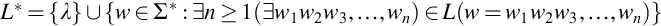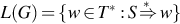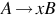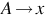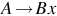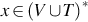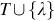Languages and Grammar
Akhil Gudivada; Dhana L. Rao1 East Carolina University, Greenville, NC, United States
1 Corresponding author: email address: raodh15@ecu.edu
Abstract
The goal of this chapter is to describe grammars for formal languages. First, we describe a mathematical notation for describing grammars. Next, we discuss the grammar classes and the corresponding languages that these grammars generate. Lastly, we outline a simplistic grammar for English language.
Keywords
English language grammar; Natural languages; Regular languages; Context-free languages; Context-sensitive languages; Chomsky hierarchy; Sentence parsing; Programming language grammar; Syntactic structures; Semantic structures
1 Introduction
There are two types of languages: natural and formal. Natural languages are those that evolved naturally in human societies through use and repetition, rather than a formal process. Formal languages are distinguished from natural languages, which are designed for special purposes such as programming computers and expressing logic. Natural languages take different forms including spoken, sign, and written. According to Ethnologue (SIL International, 2018), there are 7097 known living languages. Ethnologue is an active research spanning over six decades. A vast wealth of information on languages is available online through an Ethnologue subscription service, or via print publications: languages of Asia (Simons and Fennig, 2017a), Africa and Europe (Simons and Fennig, 2017b), and the Americas and the Pacific (Simons and Fennig, 2017c).
There are hundreds of formal languages, and programming languages dominate this category. TIOBE programming community index (TIOBE, 2018) is an indicator of the popularity of programming languages. It tracks 100 popular languages and updates the index monthly. In both natural and formal languages, the grammaticality of sentences is governed by a set of rules known as language grammar. Generative grammar is a linguistic theory which views grammar as a system of rules, and these rules determine how the words in a language are combined to form grammatical sentences in the language. Grammars of programming languages can be defined rigorously and concisely using mathematical formalisms (Linz, 2017; Rich, 2007). In contrast, it is difficult to specify grammars for natural languages concisely.
A language is a set of strings over an alphabet. An alphabet, denoted Σ, is a finite set of symbols or characters. A string is a finite sequence of symbols/characters drawn from the alphabet Σ. For example, Σ = {0, 1} is the alphabet of binary strings. The binary strings {0, 1, 01, 10, 11, 1111, 01010101111, …} are formed by concatenating the symbols in any order. The empty string, denoted ϵ, is the shortest string and contains no symbols. The notation λ is also used to denote empty strings. The set of all possible strings over Σ is denoted by Σ*.
Symbols can be anything—shapes of geometric figures, music symbols, words in a language. Symbols are basic building blocks at a right level of abstraction. For English language, the 26 lowercase and 26 uppercase letters, 10 decimal digits, punctuation, and other characters can be viewed as symbols. These symbols are used to generate words. In contrast, words in a language can also be regarded as symbols. Symbols at this level of abstraction enable investigating the generation of sentences in the language. A rule set (aka grammar) determines how the words are sequenced to generate grammatically correct sentences in the language.
Several functions can be defined on strings. The first one is the length of a string s, denoted 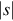 , which is the number of symbols in the string. For example,
, which is the number of symbols in the string. For example, 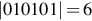 and
and 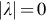 . Strings can be concatenated or appended. The concatenation operation is associative and is denoted by ∥. If the string x = natural and y = language, then
. Strings can be concatenated or appended. The concatenation operation is associative and is denoted by ∥. If the string x = natural and y = language, then 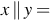 natural language. Next is the replication function, which replicates itself a specified number of times. For example, replicate (1010, 3) = 101010101010. The reversal of a string w, denoted wR, is defined as:
natural language. Next is the replication function, which replicates itself a specified number of times. For example, replicate (1010, 3) = 101010101010. The reversal of a string w, denoted wR, is defined as:
This is a recursive definition for string reversal. The reverse of a string is the last character concatenated with the reversal of the remaining string. Since we defined a language as a set of strings, standard set operations—union, intersection, difference, and complement (wrt Σ* as the universe)—are also meaningful for application to languages. The Kleene star of L, denoted by L*, is the set of strings formed by concatenating together zero or more strings of L. More formally,
In general, the grammar of a language focuses on the syntactic aspects. It is also useful to have a function which map each string to its precise meaning. Such functions are called semantic interpretation functions. Since the number of strings in most languages is infinite, it is impossible to map each string to its meaning. Instead, we are interested in functions that compute the meaning for the language's most fundamental units, and combine these meanings to compute meanings for larger expressions. Such functions are called compositional semantic interpretation functions.
1.1 Three Aspects of Languages
The three aspects are language generation, recognition, and parsing. As indicated earlier in this section, grammar is a formal mechanism for generating grammatically correct strings/sentences in the language. As we will see later, a grammar can generate infinite number of strings. Recognition is complementary to generation. Given a sentence, the task of a recognizer is to determine whether or not the sentence is a valid string in the language. The recognizer produces just a binary response. In contrast, given a grammatically correct string, a parser will outline all the steps involved in generating the string from the language grammar. Given an ungrammatical string, the parser is also expected to provide helpful information on why the string is ungrammatical.
1.2 Chapter Organization
The overarching goal of this chapter is to discuss the mechanisms used to describe grammars for formal languages. The chapter is organized as follows. Grammars of formal languages are presented in Section 2. The grammar classes and the corresponding languages are discussed in Section 3. A simplistic grammar for English language is outlined in Section 4. Finally, Section 5 concludes the chapter.
2 Formal Grammars
Recall that a grammar is a formalism for describing the strings in a language.
Our notation for describing grammars in this section is based on Linz (2017). The productions P are the core component of a grammar. They specify how strings are transformed from one form to another, beginning with the start variable S. The rules are of the form 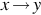 , where x is an element of
, where x is an element of 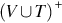 and y is in
and y is in 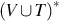 . In other words, x is the concatenation of one or more elements from the set
. In other words, x is the concatenation of one or more elements from the set 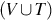 , and y is the concatenation of zero or more elements from the same set. Consider the string w of the form uxv and the production
, and y is the concatenation of zero or more elements from the same set. Consider the string w of the form uxv and the production 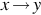 . Since the left-hand side of
. Since the left-hand side of 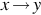 matches with a substring of w, the production is applicable to w. Then the production can be used to rewrite w to generate the new string z = uyv. The rewrite essentially involves replacing x (i.e., the left-hand side of the production rule) with y (i.e., the right-hand side of the production rule).
matches with a substring of w, the production is applicable to w. Then the production can be used to rewrite w to generate the new string z = uyv. The rewrite essentially involves replacing x (i.e., the left-hand side of the production rule) with y (i.e., the right-hand side of the production rule).
The process of deriving z from w is denoted by 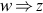 . An applicable production rule may be as often as desired. If wn is derived from w1 through the sequence of transformations
. An applicable production rule may be as often as desired. If wn is derived from w1 through the sequence of transformations 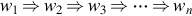 , the notation
, the notation 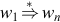 denotes that transformation. The * indicates that wn is derived from w1 through an unspecified number of steps (including zero steps).
denotes that transformation. The * indicates that wn is derived from w1 through an unspecified number of steps (including zero steps).
A grammar can potentially generate an infinite number of strings by applying the production rules in arbitrarily different orders. The notation L(G) denotes all the (terminal) strings generated by the grammar G. In other words, L(G) is the language of grammar G.
If w ∈ L(G), then the sequence 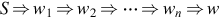 is called the derivation of the sentence w. The strings S, w1, w2, ⋯ , wn, which contain both variables and terminals are referred to as sentential forms of the derivation.
is called the derivation of the sentence w. The strings S, w1, w2, ⋯ , wn, which contain both variables and terminals are referred to as sentential forms of the derivation.
3 Grammar Classes and Corresponding Languages
Shown in Table 1 are Chomsky's four types of grammars, the class of language each grammar generates, constraints on the production rules, and the type of automaton that recognizes the strings generated by the grammars.
Table 1
| Grammar | Language Class | Rule Constraints | Recognition automaton |
|---|---|---|---|
| Type 3 | Regular | 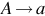 and and 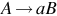 | Finite State Automaton (FSA) |
| Type 2 | Context-free | 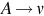 | Nondeterministic Pushdown Automaton (PDA) |
| Type 1 | Context-sensitive | 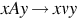 | Linear-bounded nondeterministic Turing machine |
| Type 0 | Recursively enumerable | 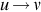 | Turing machine |

A and B are nonterminals; a: terminal; x and y are strings of terminals and nonterminals, and can be empty; ν is a string of terminals and nonterminals, and cannot be empty.
Not shown in the table is the set of grammars that generate recursive languages, and these grammars fall between Type 0 and Type 1. Every regular language is also a context-free language, every context-free language is also context-sensitive, every context-sensitive language is also recursive, and every recursive language is also recursively enumerable. These inclusions are proper subsets. That is, there are context-sensitive languages that are not regular, context-sensitive languages that are not context-free, and so on.
Type 0 grammars place no restrictions on the form of production rules and include all formal languages. These grammars generate exactly those languages that can be recognized by a Turing machine—recursively enumerable, or Turing-recognizable languages. As we go from Type 0 to Type 3, additional restrictions are placed on production rules; also, the automata that accept languages generated by the grammars become simpler in structure and function.
3.1 Regular Languages
First, we describe deterministic Finite State Automata (DFA), which accepts all languages generated by Type 3 grammars. Shown in Fig. 1 is a DFA which recognizes/accepts all natural numbers that are divisible by 3. This DFA is constructed using JFLAP, which is an open-source software for creating and testing various classes of automata (Rodger and Finley, 2006).
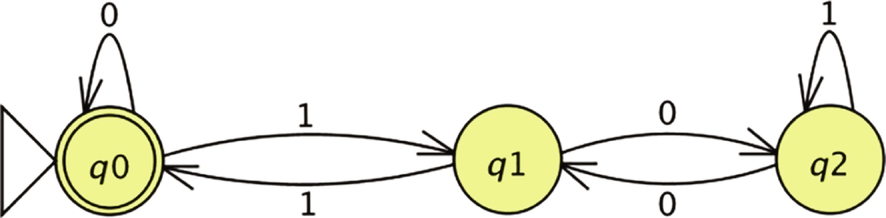
The input to DFA is the binary number representation of a natural number. A DFA has a finite number of states. The DFA in Fig. 1 has three states: q0, q1, and q2. One of these states is designated as the start state (q0, indicated by the left-pointing triangle), and the other as the final/accepting state (q0, indicated by the circle with double border). There can be only one start state, but multiple final/accepting states. DFA transitions from one state to another state depending on the current state and the input symbol read.
When DFA starts, it is in the start state, q0. It reads one input symbol at a time. Consider 110 as input to the DFA. When the first 1 is read, DFA transitions from q0 to q1. Next, when the second 1 is read, DFA transitions from q1 back to q0. Lastly, when 0 is read, DFA remains in state q0 (indicated by the self-loop of state q0). Now the DFA has consumed all the input and halted in q0, which is a final state. Therefore, the DFA has recognized the string 110, which means that the binary string 110 is divisible by 3. If the DFA consumes all input and halts in a nonfinal state, we say that the DFA rejected the string. Such binary strings are not divisible by 3. The reader may verify that the DFA will reject the string 1010, whereas the string 101110011101101110011101 will be accepted.
Regular languages can be described using three equivalent formalisms: Finite State Automata (FSA), regular grammars, and regular expressions. We have seen above an FSA that accepts all natural numbers that are divisible by 3. The language recognized/accepted by that FSA are binary string representation of all natural numbers that are divisible by 3. The regular languages are a family of languages which are accepted by FSA.
Regular grammars are written in one of two standard forms: right-linear, or left-linear.
Let G = (V, T, S, P) be a right-linear grammar. Then the language generated by L(G) is a regular language. Also, let L be a regular language on the alphabet Σ. There exists a right-linear grammar G = (V, E, S, P) such that L = L(G). Similar statements can be made about left-linear grammar. Therefore, regular grammars and regular languages are equivalent. Without proof, we state that a language L is regular if and only if there exists a left-linear grammar G such that L = L(G). Equivalently, a language L is regular if and only if there exists a right-linear grammar G such that L = L(G).
3.2 Context-Free Languages
Regular languages are effective in describing certain simple patterns. For example, they are used for specifying search/replace operation in text editors. Consider the language L = {anbn : n ≥ 0}, which is a nonregular language. This language is nonregular because there is no DFA which can accept strings of this language (Linz, 2017). However, such a language is useful for describing fully parenthesized arithmetic expressions, for example. Intuitively, an FSA has finite number of states, where as the language L requires memorizing how many a’s it has seen before encountering the first b, and the n can be arbitrarily large. Therefore, we need languages that are more powerful/expressive than the regular languages. This leads us to context-free languages and grammars.
Recall the restrictions on the productions in regular grammars. The left-hand side must be a single variable, while the right-hand side has a special form. We must relax some of these restrictions to create more powerful grammars, and hence more expressive languages. We retain the restriction on the left-hand side, but permit anything on the right-hand side to get context-free grammars (CFGs) (Linz, 2017).
CFGs allow a nonterminal to be replaced by a corresponding production rule whenever the nonterminal appears in a sentential form. This replacement can be done irrespective of what precedes or follows the nonterminal. Recall that CFGs allow only one nonterminal on the left-hand side of production rules (see Table 1).
The class of languages generated by the CFGs is quite significant. For many programming languages, a context-free language describes the set of syntactically correct statements. The language that describes the set of well-formed Boolean queries is also a context-free language. Even for natural languages such as English, most syntactic constructions can be described using context-free languages.
3.2.1 A Context-Free Grammar for Arithmetic Expressions
CFGs comprise a category of grammars (more on this in Section 3). We illustrate how a CFG is used to generate strings of a language. The CFG is shown in Table 2. The metasymbol, :=, should be read as “is defined as.” Using this CFG, we can generate arithmetic expressions of arbitrary complexity. Operands in the arithmetic expressions are integers, and operators include addition (+), subtraction (−), multiplication (*), division (/), and exponentiation (∧).
Table 2
| Production Rule | Meaning |
|---|---|
| <expr> ::= <term> [ <expr1> ]* | An expression is a term followed by zero or more occurrences of expressions of type 1 |
| <expr1> ::= (+ ∣ -) <term> | An expression of type 1 is a + (plus) or − (minus) followed by zero or more occurrences of term |
| <term> ::= <factor> [ <expr2> ]* | An term is a factor followed by zero or more occurrences of expressions of type 2 |
| <factor> ::= <base> [ <expr3> ]* | A factor is a base followed by zero or more occurrences of expressions of type 3 |
| <base> ::= ( <expr> ) ∣ <number> | A base is an expression enclosed in parentheses or an occurrence of number |
| <expr2> ::= (* ∣ /) <factor> | An expression of type 2 is * (multiplication) or / (division) enclosed in parentheses followed by a factor |
| <expr3> ::= ∧ <exponent> | An expression of type 3 is a ∧ (exponentiation) followed by an exponent |
| <exponent> ::= ( <expr> ) ∣ <number> | An exponent is an expression enclosed in parenthesis or a number |
| <number> ::= <digit> [ <digit> ]* | A number is a digit followed by zero or more occurrences of number |
| <digit> ::= 0 ∣ 1 ∣ 2 ∣ 3 ∣ 4 ∣ 5 ∣ 6 ∣ 7 ∣ 8 ∣ 9 | A digit is one of the 10 decimal digits |
A graph-based representation is used for efficiently generating arithmetic expressions in a controlled manner from CFG grammars (Gudivada et al., 2017). We refer to this as the grammar graph and is shown in Fig. 2. This is similar to a Deterministic Finite State Automata (DFSA) but the semantics are different (Rich, 2007). The grammar graph consists of a set of vertices and edges. The color coding, line types, and other markers capture critical information to aid the generation of arithmetic expressions. Each vertex in the graph corresponds to a terminal or nonterminal in the grammar. In Fig. 2, there is only one terminal designated by the vertex labeled <digit>. Note the color of the vertex.
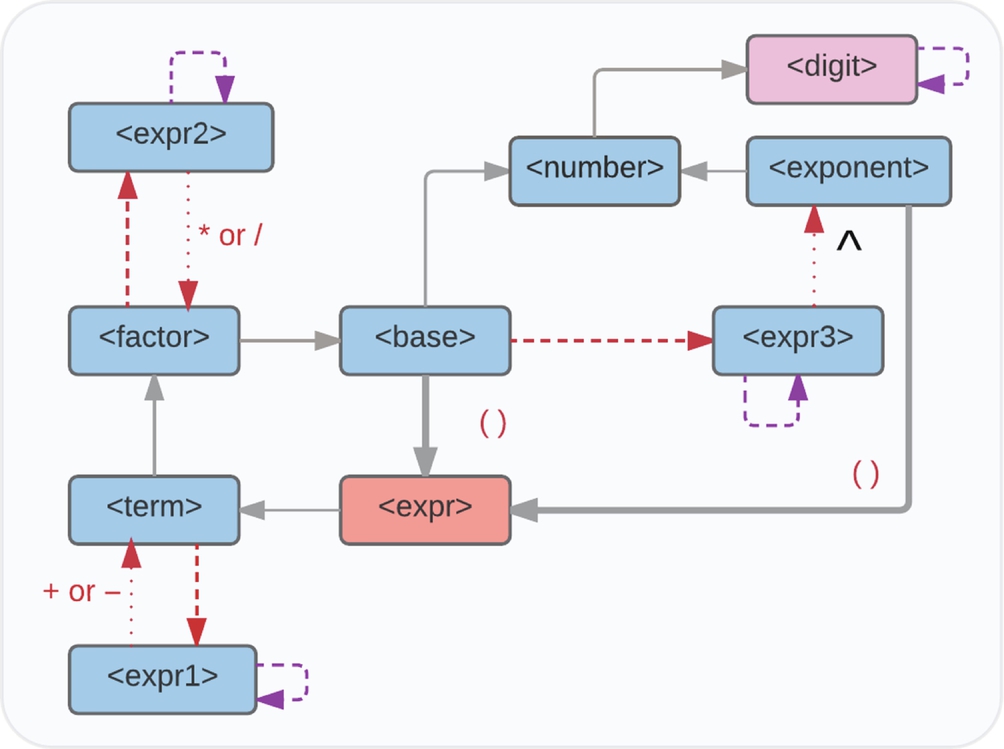
The graph node labeled <expr> is the start vertex for expression generation. The directed edge from <expr> to <term> indicates a substitution—the nonterminal <expr> is replaced by another nonterminal <term>. Next, consider the red-dashed directed edge from <term> to <expr1>. This denotes an optional edge and does not involve replacing <term> with <expr1>. The optional edge semantic is that whatever is generated through the optional edge gets appended to the <term>. In other words, instead of replacement, something gets appended to the <term>.
The loop on the vertex labeled <expr1> denotes that zero or more copies of <expr1> are appended to <expr1>. Next, consider the red-dotted directional edge from <expr1> to <term>. Notice the edge label: plus (+) or minus (−). The semantic is that each copy of <expr1> is replaced by prefixing <term> with plus (+) or minus (−). For example, <expr1> can be replaced by either + <term> or − <term>. Lastly, consider the thick-lined directed edge from <base> to <expr> and note the edge label: ( ). The semantic of this notation is that <base> is replaced by <expr> enclosed in parenthesis. That is, <base> is replaced by ( <expr> ).
Consider generating an arithmetic expression of the form: 32 + 65 − 173. As noted earlier, the generation process always starts at the vertex named <expr>. Next, since there is an edge from <expr> to <term>, we replace <expr> by <term>. Traversal of the edge from <term> to <expr1> is optional. If this path is chosen, we append to <term> rather than replacing it. We choose this optional edge and visit <expr1>. The loop indicates zero or more repetitions and each repetition generates one <expr1>. Let us generate two copies—<expr1> <expr1>. Next, consider the edge from <expr1> to <term>. Each copy of <expr1> will be replaced by a plus (+) or a minus (−) followed by the <term>. Assume that we chose plus in the first case and minus in the second case. Now we have the string <term> + <term> − <term>. Next, using the edge from <term> to <factor>, each copy of <term> is replaced by <factor> yielding <factor> + <factor> − <factor>. Similarly, we traverse from <factor> to <base> yielding <base> + <base> − <base>. Repeating this one more time using the edge from <base> to <number>, we get <number> + <number> − <number>. Using the <number>—<digit> directed edge and looping on the <digit>, each <number> in <number> + <number> − <number> can be replaced by a desired integer number, which yields 32 + 65 − 173. Using a similar procedure, we can generate any number of arbitrarily complex arithmetic expressions such as 9∧((8*9)∧5*(8*((5*(7∧(09/95)/9))+(9−(4∧(((6∧9)+2)+((81/877)∧5)∧9)))+8)∧3+8))/8.
In the grammar graph, we distinguish between two types of paths: simple and complex. All paths start at the special vertex <expr> and end at a terminal vertex (e.g., <digit>). A simple path is one that does not involve any loops or optional edge traversals. For example, <expr>  <term>
<term>  <factor>
<factor> 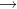 <base>
<base> 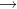 <number>
<number> 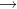 <digit> is a simple path. Simple path traversals yield the simplest arithmetic expressions such as 4 and 6. Complex paths are generated from simple paths by adding optional traversals, single-, and multivertex loops. For instance, adding a single vertex loop, we can generate expressions such as 15 and 5674. An example of a multivertex loop is <expr>
<digit> is a simple path. Simple path traversals yield the simplest arithmetic expressions such as 4 and 6. Complex paths are generated from simple paths by adding optional traversals, single-, and multivertex loops. For instance, adding a single vertex loop, we can generate expressions such as 15 and 5674. An example of a multivertex loop is <expr> 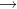 <term>
<term> 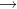 <factor>
<factor> 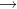 <base>
<base> 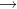 <expr>.
<expr>.
3.3 Parse Trees
A parse tree (aka derivation tree) is a graphical representation that depicts how strings in a language are derived using the language grammar. It is an ordered tree in which nodes are labeled with the left-hand sides of the productions, and the children of the nodes represent the corresponding productions’ right-hand sides. Consider the production 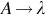 , where A is a nonterminal and λ is the empty string (i.e., a string whose length is 0). Such productions are called null productions, since they allow a nonterminal to be eliminated trivially. A tree has two types of nodes or vertices: internal (aka nonleaf nodes) and external (aka leaf nodes).
, where A is a nonterminal and λ is the empty string (i.e., a string whose length is 0). Such productions are called null productions, since they allow a nonterminal to be eliminated trivially. A tree has two types of nodes or vertices: internal (aka nonleaf nodes) and external (aka leaf nodes).
Consider a tree that has properties (c), (d), and (e), but (a) does not necessarily hold. In such trees, we obtain a partial derivation tree by replacing (b) with the following: 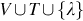 .
.
The yield of a parse tree is the string of symbols obtained by reading the leaf nodes of the tree from left to right, and omitting any λ’s encountered. There is equivalence between sentential forms and derivation trees. Let G be a CFG and L(G) is the language generated by G. Then for every w ∈ L(G), there exists a derivation tree of G whose yield is w. Conversely, the yield of any derivation tree is in L(G). Further, if tG is any partial derivation tree for G whose root is labeled S, then the yield of tG is a sentential form of G.
3.3.1 Programming Languages and Parsing
Like the English language, syntax and semantics are associated with programming languages. The syntax of a programming language specifies how to construct syntactically correct programs. In other words, the syntax specifies the structure of strings in the language. At the highest level, a computer program is just one syntactic unit, which may be comprised of other syntactic units. Unlike English, grammars associated with programming languages are concise, precise, and formal. They need to be concise so that the grammar can be succinctly described and easily understood, precise so that there is no ambiguity in their specification, and formal so that they are amenable for checking the syntactic correctness of programs by a compiler. BNF or EBNF are used to describe grammars of programming languages.
The notation used for describing programming language grammars is slightly different from that which we have seen earlier in this chapter. This notation is referred to as Backus–Naur Form (BNF) or extended BNF (EBNF). BNF (Backus–Naur Form) is a syntactic metalanguage (i.e., a language about a language). The metalanguage is a formal notation for specifying the grammar that describes the syntax of a programming language. BNF was originally developed by John Backus and subsequent contribution from Peter Naur to describe the syntax of Algol 60 programming language. A few enhancements have been made to BNF resulting in Enhanced BNF (EBNF). EBNF is more succinct than BNF. However, BNF and EBNF are equivalent in terms of their expressiveness.
EBNF employs a number of rules for describing a programming language. Each rule names a syntactic unit of the language and describes possible forms for a syntactic unit. EBNF also specifies which sequence of symbols is valid in the language. Syntactic units are also referred to as symbols of the language. There are two types of symbols: terminal and nonterminal. A nonterminal symbol is described in terms of other nonterminal (including itself) and terminal symbols. A terminal symbol is an atomic value which cannot be further decomposed into smaller components of the language.
Like any other formal language, the syntax of programming languages are defined by CFGs. An identifier is a name that is used to uniquely identify syntactic units of a program—variables, keywords, methods, method parameters, among others. Consider the following rule for an identifier: it must begin with a letter, @ character, or underscore followed by one or more letters or digits. Table 3 shows how this rule is expressed in EBNF.
Table 3
| Digit | := | 0 | 1 | ⋯ | 9 |
| Letter | := | _ | a | b | c | ⋯ | z | A | B | C | ⋯ | Z |
| Identifier | := | letter {letter | digit}| @ {letter | digit}+ |
Each row in the table defines a production rule for a nonterminal symbol: digit, letter, and identifier. The nonterminal letter is defined in terms of 53 terminal symbols: _, a, b, c, ⋯, z, A, B, C, ⋯, Z. The three center dots (⋯) is a notation to represent the intermediate values of the sequence. In other words, the letter can be replaced by an underscore, or by any one of lower or upper case alphabet. Terminal symbols are typeset in bold face. Sometimes, the terminal symbols are represented within quotes (e.g., “a”) to facilitate representing EBNF without dependence on text formatting such as bold and emphasized.
The last row defines identifier as: either a letter followed by zero or more occurrences of letters or digits, or @ followed by one or more occurrences of letters or digits. The metasymbol pair {and} indicates zero or more occurrences of a letter or digit. The choice between a letter or digit is indicated by the metasymbol |. The rule says that an identifier cannot begin with a digit; just an underscore (i.e., _) by itself is a valid identifier; if the identifier starts with @, then it must be followed by one or more occurrences of letters or digits. Table 4 lists the meaning of various metasymbols that EBNF uses.
Table 4
| Metasymbol | Description |
|---|---|
| := | Is defined as |
| | | Choice |
| [ ] | Optional |
| { } | Repetition, zero or more times |
| { }+ | Repetition, one or more times |
| ( ) | Group items together, in mathematical sense |
| ? | The symbol (or group of symbols in parentheses) to the left of ? is optional (i.e., can appear 0 or 1 time) |
Given a string w in a language whose grammar is G, we would like to determine whether or not w is in L(G). If w ∈ L(G), we would also like to find a derivation of w. The term parsing refers to determining a sequence of productions by which a w is generated from G. For every CFG G, there exists an algorithm that parses any w ∈ L(G) in time 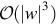 .
.
3.4 Context-Sensitive Languages
A number of grammars can be defined between the restricted and context-free grammars. Context-sensitive grammars are one such class. These grammars generate languages that can be recognized with a restricted class of Turing machines called linear-bounded automata. A grammar G = (V, T, S, P) is context-sensitive if all productions are of the form 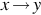 , where
, where 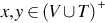 and
and 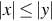 . These grammars are noncontracting (i.e.,
. These grammars are noncontracting (i.e., 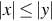 ) as length of successive sentential forms can never decrease.
) as length of successive sentential forms can never decrease.
It has been shown that all context-sensitive grammars can be written in a normal form in which all productions are of the form: 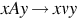 . The name context-sensitive comes from the fact that the production
. The name context-sensitive comes from the fact that the production 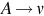 can only be applied in contexts where x occurs to the left of A and y occurs to the right of A. A language L is context-sensitive if there exists a context-sensitive grammar G such that
can only be applied in contexts where x occurs to the left of A and y occurs to the right of A. A language L is context-sensitive if there exists a context-sensitive grammar G such that 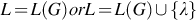 . Also, for every context-sensitive language L not including λ, there exists some linear-bounded automaton M such that L = L(M). Furthermore, if a language L is accepted by some linear-bounded automaton M, then there exists a context-sensitive grammar that generates L. Lastly, every context-sensitive language L is recursive, and there exists a recursive language that is not context-sensitive.
. Also, for every context-sensitive language L not including λ, there exists some linear-bounded automaton M such that L = L(M). Furthermore, if a language L is accepted by some linear-bounded automaton M, then there exists a context-sensitive grammar that generates L. Lastly, every context-sensitive language L is recursive, and there exists a recursive language that is not context-sensitive.
3.5 Recursively Enumerable and Recursive Languages
Recall that Type 0 grammars are unrestricted. A grammar G = (V, T, S, P) is called unrestricted if all the productions are of the form 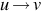 , where
, where 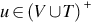 and
and 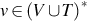 . Any language generated by an unrestricted grammar is recursively enumerable. Furthermore, for every recursively enumerable language L, there exists an unrestricted grammar G, such that L = L(G). In other words, the family of languages associated with unrestricted grammars is same as the family of recursively enumerable languages. Equivalently, a language L is recursively enumerable if there exists a Turing machine that accepts L. For every string w ∈ L, the Turing machine will halt in a final state. However, what happens when the machine is given a string that is not in L? Will it halt in a nonfinal state, or it never halts and enters an infinite loop? These questions lead us to the definition of recursive languages. A formal language L is recursive if there exists a total Turing machine—the one that halts on every given input—which given a finite sequence of symbols as input, accepts the input if it belongs to the language L and rejects the input otherwise. Recursive languages are also referred to as decidable languages.
. Any language generated by an unrestricted grammar is recursively enumerable. Furthermore, for every recursively enumerable language L, there exists an unrestricted grammar G, such that L = L(G). In other words, the family of languages associated with unrestricted grammars is same as the family of recursively enumerable languages. Equivalently, a language L is recursively enumerable if there exists a Turing machine that accepts L. For every string w ∈ L, the Turing machine will halt in a final state. However, what happens when the machine is given a string that is not in L? Will it halt in a nonfinal state, or it never halts and enters an infinite loop? These questions lead us to the definition of recursive languages. A formal language L is recursive if there exists a total Turing machine—the one that halts on every given input—which given a finite sequence of symbols as input, accepts the input if it belongs to the language L and rejects the input otherwise. Recursive languages are also referred to as decidable languages.
There are languages that are not recursively enumerable. It has been shown that there are fewer Turing machines than there are languages. This implies that there are some languages that are not recursively enumerable. Lastly, there are languages that are recursively enumerable, but not recursive. The family of recursive languages is a proper subset of recursively enumerable languages.
4 A Simplistic Context-free Grammar for English Language
CFGs are used as models of syntax for both natural and programming languages. The notion of constituency plays a critical role in developing grammars. Constituency refers to the abstraction that groups of words behave as single units/constituents. A significant aspect of developing grammar for a natural language lies in discovering constituents present in the language. Examples of constituents include noun phrases, verb phrases, and prepositional phrases. A noun phrase refers to a sequence of words surrounding one or more nouns.
Consider a CFG, G = (V, T, P, S), where V = {S, NP, VP, Vi, Vt, IN, NN, PP, DT}, T = {the, dog, chased, cat, perched, on, tree, sneeze}, S is the start symbol (i.e., sentence), and P are production rules. The meaning of the remaining elements in V is: NP is noun phrase; VP is verb phrase; Vi is intransitive verb; Vt is transitive verb; IN is preposition; NN is noun; PP is prepositional phrase; and DT is determiner. The production rules P are shown in Table 5.
Table 5
| Production Rule | Meaning |
|---|---|
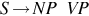 | A sentence is a noun phrase followed by a verb phrase |
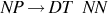 | A noun phrase is a determiner followed by a noun |
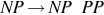 | A noun phrase can also be another noun phrase followed by a prepositional phrase |
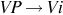 | A verb phrase is simply an intransitive verb |
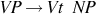 | A verb phrase is a transitive verb followed by a noun phrase |
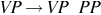 | A verb phrase can also be another verb phrase followed by a prepositional phrase |
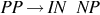 | A prepositional phrase is a preposition followed by a noun phrase |
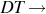 the the | The is a determiner |
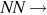 dog ∣ cat ∣ tree dog ∣ cat ∣ tree | Dog, cat, and tree are nouns |
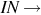 on on | On is a preposition |
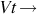 chased ∣ perched chased ∣ perched | Both chased and perched are transitive verbs |
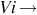 sneeze sneeze | Sneeze is an intransitive verb |
Recall that for every CFG, parsing algorithms exist. English language sentences can be parsed using such algorithms. In conclusion, what we have presented in this section is a very simplistic CFG for English language. In reality, the CFG will consists of hundreds of production rules.
5 Summary
This chapter presented an overview of types of grammars and associated languages. We discussed how to specify grammars for regular, context-free, context-sensitive, and recursively enumerable languages. We concluded the chapter with a simplistic grammar for the English language.