Do not refer to the text when taking this test. You may draw diagrams or use a calculator if necessary. A good score is at least 30 correct. Answers are in the back of the book. It’s best to have a friend check your score the first time, so you won’t memorize the answers if you want to take the test again.
1. Which of the following represents an arithmetic sequence?
(a) 0, 1, 2, 4, 8, 16, 32
(b) 2, 5, 8, 11, 14, 17, 20
(c) 1, −1, 1, −1, 1, −1, 1
(d) 1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7
(e) 1, 1/2, 1/4, 1/8, 1/16, 1/32, 1/64
2. A car is advertised as being capable of going from 0 to 60 miles per hour in 5 seconds. What is the average acceleration, in miles per hour per second (mi/hr/s) that this figure represents?
(a) 5 mi/hr/s
(b) 10 mi/hr/s
(c) 12 mi/hr/s
(e) More information is necessary to calculate it.
3. Suppose that when you “floor” the gas pedal in your car, it produces a certain constant forward force. This results in a certain forward acceleration when you’re all alone in the car. If you fill up the car with passengers so its mass increases by 25% compared to its mass when you are alone in it, and then you “floor” the gas pedal, what happens to the forward acceleration? Ignore any possible effects of friction. Remember that force is the product of mass and acceleration.
(a) The acceleration becomes 1.25 times as great as it is with only you in the car.
(b) The acceleration stays the same as it is with only you in the car.
(c) The acceleration becomes 4/5 times as great as it is with only you in the car.
(d) The acceleration becomes 3/4 as great as it is with only you in the car.
(e) The acceleration becomes half as great as it is with only you in the car.
4. Suppose that when you “floor” the gas pedal in your car, it produces a certain constant forward force. This results in a certain forward acceleration when you’re all alone in the car. If you put high-performance fuel in the tank, producing a 25% increase in the force produced when you “floor” the gas pedal, what happens to the forward acceleration when you are alone in the car and you “floor” the gas pedal? Ignore any possible effects of friction. Remember that force is the product of mass and acceleration.
(a) The acceleration stays the same as it is with the ordinary fuel.
(b) The acceleration becomes 1.25 times as great as it is with the ordinary fuel.
(c) The acceleration becomes 1.563 times as great as it is with the ordinary fuel.
(d) The acceleration becomes twice as great as it is with the ordinary fuel.
(e) The acceleration becomes four times as great as it is with the ordinary fuel.
5. A quantity that has magnitude and direction is known as
(a) a variable
(b) a constant
(d) a vector
(e) a logarithm
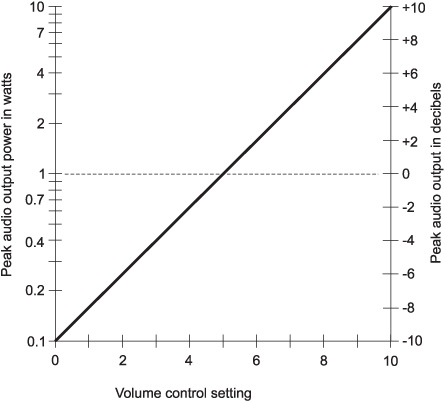
6. Imagine that you’ve purchased a new hi-fi audio amplifier for your car. It contains volume (or gain) control knobs, one for each channel, calibrated in numbers from 0 to 10. The specification sheet in the instruction manual for your new amplifier contains a graph that looks like Fig. Test 4-1. From this graph, it is apparent that
(a) the output volume, in watts, is directly proportional to the volume control setting in either channel
(b) the output volume, in decibels, is directly proportional to the volume control setting in either channel
(c) the output volume, in watts, is inversely proportional to the volume control setting in either channel
(d) the output volume, in decibels, is inversely proportional to the volume control setting in either channel
(e) the output volume increases according to the square of the volume control setting in either channel

Fig. Test 4-1. Illustration for Part Four Test Questions 6 through 8.
7. Suppose you’re listening to music using the amplifier whose specifications include a graph such as that shown in Fig. Test 4-1. If you increase the volume control setting by 2 units, the peak output power, in watts, increases by
(a) 0.2 watts
(b) 0.4 watts
(c) 2 watts
(d) 4 watts
(e) an amount that depends on the initial setting.
8. Suppose you’re listening to music using the amplifier whose specifications include a graph such as that shown in Fig. Test 4-1. If you increase the volume control setting by 2 units, the peak output power, in decibels, increases by
(a) 0.2 decibels
(b) 0.4 decibels
(c) 2 decibels
(d) 4 decibels
(e) an amount that depends on the initial setting
9. The sum of all the terms in a sequence is called
(a) a partial sum
(b) a series
(c) an arithmetic sequence
(d) a geometric sequence
(e) a linear sequence
10. Which of the following is always a scalar quantity?
(a) The velocity of a train.
(b) The acceleration of a car.
(c) The impulse produced by a rocket engine.
(d) The mass of a truckload of bricks.
(e) The force produced by the wind against a wall.
11. Suppose you’re driving a motorboat across a river. The bow of the boat is pointing straight south, and your water speed is 7 knots. There is a steady current in the water moving from east to west at a speed of 7 knots. What is your direction (heading) relative to land?
(a) South.
(b) Southeast.
(c) Southwest.
(d) East.
(e) West.
12. Suppose you’re driving a motorboat across a river. The bow of the boat is pointing straight north, and your water speed is 12 knots. There is a steady current in the water moving from west to east at a speed of 9 knots. What is your speed relative to land?
(a) 3 knots.
(b) 9 knots.
(c) 12 knots.
(d) 15 knots.
(e) It is impossible to tell without more information.
13. Suppose you buy a house for $200,000. You are confident that its value will increase by exactly 10% per year for the next 10 years. According to this formula, what should the house be worth after 3 years?
(a) $230,000
(b) $242,000
(c) $260,000
(d) $266,200
(e) More information is necessary to answer this question.
14. Suppose you buy a house for $200,000, and its value falls by exactly 10% per year for 3 years. What is the house worth at the end of the 3 years?
(a) $170,000
(b) $162,000
(c) $145,800
(d) $140,000
(e) More information is necessary to answer this question.
15. Which of the following can be expressed as a vector quantity?
(a) The mass of a bag of apples.
(b) The brightness of a source of light.
(c) The loudness of a sound.
(d) The acceleration of a car.
(e) The volume of water in a swimming pool.
16. In Fig. Test 4-2, which of the vectors in the lower diagrams best represents the velocity vector for the car shown in the top diagram? Imagine the car moving generally from left to right along the road as shown. Assume each division represents 5 meters per second.
(a) a
(b) b
(c) c
Fig. Test 4-2. Illustration for Part Four Test Questions 16 through 18.
(d) d
(e) e
17. In Fig. Test 4-2, which of the vectors in the lower diagrams best represents the acceleration vector for the car shown in the top diagram? Imagine the car moving generally from left to right along the road as shown. Assume each division represents 5 meters per second squared.
(a) a
(b) b
(c) c
(d) d
(e) e
18. Imagine the car reversing direction as shown in the diagram of Fig. Test 4-2, so it moves generally from right to left at a constant speed of 15 meters per second. Which of the vectors in the lower diagrams best represents the acceleration vector in this case? Assume each division represents 5 meters per second squared.
(a) a
(b) b
(c) c
(d) d
(e) e
19. Suppose Jimsville is 60 miles from Joesville. You need to get from one town to the other in 90 minutes or less. Your minimum average speed
(a) must be 30 miles per hour
(b) must be 40 miles per hour
(c) must be 45 miles per hour
(d) must be 60 miles per hour
(e) cannot be determined from this information
20. Suppose Jimsburg is 80 kilometers from Joesburg. You make a trip from one town to the other in exactly 80 minutes. Your instantaneous acceleration
(a) must be at least 1 meter per second squared
(b) must be at least 60 meters per second squared
(c) must be at least 16.17 millimeters per second squared
(d) must be at least 16.67 meters per second squared
(e) cannot be determined from this information
21. Suppose you deposit exactly $65,536.00 into an account on the first day of the month. On the second day of the month, you deposit exactly half this amount. On the third day, you deposit half the amount that you deposited on the second day. You repeat this process until you can no longer cut the deposits in half while still making them in whole cents (that is, without “breaking up a penny”). What will be the amount you have in the bank at that time?
(a) $131,071.75
(b) $131,071.00
(c) $131,072.75
(d) $131,072.00
(e) That time will never be reached; the account balance will continue to increase without limit.
22. Speed can be expressed in terms of
(a) distance multiplied by time
(b) distance per unit time
(d) acceleration per unit time
(e) velocity multiplied by time
23. Any radioactive material has a specific period of time known as its half-life, over which its radioactivity drops by 50%. Suppose the half-life of element X is 100 years. Right now the radiation intensity from a sample of element X is at a certain level. In 100 years, the element X will be 50% as radioactive as it is right now. After another 100 years, the radioactivity of the element X will drop by another 50%. This process will repeat, century after century, eon after eon. The radiation-intensity levels of any given sample of element X, measured in constant “radiation units (RU)” at intervals of 100 years:
(a) increase without limit
(b) alternate between positive and negative
(c) comprise a geometric progression
(d) add up to zero
(e) converge toward 1
24. Suppose you want to check the floor in a room to see if it is perfectly horizontal. You know the floor is perfectly flat throughout the room. You have a carpenter’s level with which you can check to see if any particular line along the floor is horizontal. What is the minimum number of readings you must make with the level in order to know whether or not the floor is perfectly horizontal?
(a) 1
(b) 2
(c) 3
(d) 4
(e) 5
25. Which of the following can be a unit of acceleration magnitude?
(a) Meters per second.
(b) Seconds per meter.
(c) Meters per second squared.
(d) Seconds per meter squared.
(e) Degrees per meter squared.
26. Imagine a room whose floor and ceiling are perfectly square, and whose four walls are all perfect rectangles. Imagine one corner of this room, where two walls intersect the floor. There are three line segments that come together at this corner: the line segment where the two walls intersect, the line segment where one wall intersects the floor, and the line segment where the other wall intersects the floor. At the corner where they all come together, these three line segments are
(a) mutually parallel
(b) mutually perpendicular
(c) mutually skewed
(d) mutually equilateral
(e) none of the above
27. A flat geometric plane in 3D space can be uniquely defined by
(a) a point in the plane and a vector perpendicular to the plane
(b) three points that do not all lie on the same straight line
(c) two parallel straight lines
(d) two intersecting straight lines
(e) any of the above
28. Suppose you have a jar in which you keep change that accumulates in the course of your shopping adventures. Every day, you put 76 cents into the jar. The amount of money in the jar increases day by day, according to
(a) an arithmetic progression
(b) a geometric progression
(c) a logarithmic progression
(d) an exponential progression
(e) a convergent progression
29. Any radioactive material has a specific period of time known as its half-life, over which its radioactivity drops by 50%. Suppose the halflife of element Y is 80,000 years, someone has just handed you a sample of it, and the radiation level from it is 128 “radiation units (RU).” In 80,000 years, the sample will be half as radioactive as it is today. After another 80,000 years, the radioactivity will go down by half, again. This decay process will go on essentially forever. Suppose the maximum safe level for human exposure to any radioactive substance is 16 RU. How long will it be before it’s no longer dangerous to hang around the piece of element Y you’ve just been given?
(a) 240,000 years.
(b) 160,000 years.
(c) 80,000 years.
(d) 40,000 years.
(e) 20,000 years.
Fig. Test 4-3. Illustration for Part Four Test Questions 30 through 34.
30. What would Fig. Test 4-3 most likely represent?
(a) The frequency setting of a hi-fi stereo radio receiver.
(b) The direction in which a car or truck drives down a level street.
(c) The direction in which a broadband satellite Internet dish is pointed.
(d) The compass bearing of a hiker in the wilderness.
(e) The acceleration of a speedboat on a lake.
31. In Fig. Test 4-3, what do θx, θy, and θz represent?
(a) Direction cosines.
(b) Direction angles.
(c) Compass bearings.
(d) Elevation angles.
(e) Azimuth bearings.
32. In Fig. Test 4-3, what is represented by the lowercase, boldface letter a?
(a) A ray of light.
(b) An exponent.
(c) A logarithm.
(d) A scalar.
(e) A vector.
33. What is another thing that Fig. Test 4-3 might depict?
(a) The velocity at which a missile is fired.
(b) Sunlight shining down on the surface of the earth.
(c) The motion of a train along a level track.
(d) The speed of the wind in a hurricane.
(e) The time and temperature in a certain place.
34. The diagram in Fig. Test 4-3 portrays?
(a) 1 spatial dimension.
(b) 2 spatial dimensions.
(c) 3 spatial dimensions.
(d) 4 spatial dimensions.
(e) 5 spatial dimensions.
35. The human ear and brain perceive the loudness of a sound
(a) in proportion to the square of the sound power
(b) in proportion to the base-10 exponential of the sound power
(c) in proportion to the base-e exponential of the sound power
(d) in proportion to the logarithm of the sound power
(e) in inverse proportion to the sound power
36. Suppose we are told the following sequence S is an arithmetic sequence:
S = 80, 75, x, y, z, 55, 50
What is the difference between x and z?
(a) 5
(b) 10
(c) 15
(d) 20
(e) It cannot be determined without more information.
37. Suppose you are told that the intensity of some effect Y varies according to the 3/2 power of the strength of some other effect X. If the strength of effect X doubles, by what factor does the intensity of effect Y increase?
(a) It does not change.
(b) It doubles.
(c) It quadruples.
(d) It increases by a factor of the square root of 8.
(e) More information is needed to answer this question.
38. Suppose you are building a coffee table. Your friend wants it to have four legs attached to the table at the corners of a square. But you want it to have only three legs, attached to the table at the vertices of an equilateral triangle. You know that a three-legged table won’t wobble, even if the floor is irregular or if the legs don’t all turn out to be exactly the same length. On what geometric principle is this fact based?
(a) A vector normal to a flat plane cannot lie in that plane.
(b) Two intersecting, straight lines uniquely define a flat plane.
(c) Three points, not all on the same line, uniquely define a flat plane.
(d) Four points can lie in the same plane, but this is not always true.
(e) Four points can lie at the corners of a square, but this is not always true.
39. Suppose your computer receives (unknown to you) an e-mail worm that causes it to automatically send the same message to 100 other computers. Ninety percent (90%) of the computers that receive this e-mail block it out, but the other 10% get it and execute its nefarious instructions. This process continues indefinitely, with one iteration taking place every minute. The number of these useless, unethical, illegal e-mail messages clogging up the Internet increases, per unit minute, according to
(a) an arithmetic progression
(b) a logarithmic progression
(c) a geometric progression
(d) a quadratic progression
(e) a cubic progression
40. Suppose you step on the “gas pedal” of a high-performance car while you take a banked curve on a race track. The magnitude and direction of the acceleration of the car at a particular instant in time can be fully defined as
(a) a vector
(b) a logarithm
(c) a constant
(d) a trigonometric function
(e) an exponent