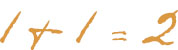
why we believe in arithmetic the world’s simplest equation
One plus one equals two: perhaps the most elementary formula of all. Simple, timeless, indisputable … But who wrote it down first? Where did this, and the other equations of arithmetic, come from? And how do we know they are true? The answers are not quite obvious.
One of the surprises of ancient mathematics is that there is not much evidence of the discussion of addition. Babylonian clay tablets and Egyptian papyri have been found that are filled with multiplication and division tables, but no addition tables and no “1 + 1 = 2.” Apparently, addition was too obvious to require explanation, while multiplication and division were not. One reason may be the simpler notation systems that many cultures used. In Egypt, for instance, a number like 324 was written with three “hundred” symbols, two “ten” symbols, and four “one” symbols. To add two numbers, you concatenated all their symbols, replacing ten “ones” by a “ten” when necessary, and so on. It was very much like collecting change and replacing the smaller denominations now and then with larger bills. No one needed to memorize that 1 + 1 = 2, because the sum of | and | was obviously ||.
In ancient China, arithmetic computations were performed on a “counting board,” a sort of precursor of the abacus in which rods were used to count ones, tens, hundreds, and so on. Again, addition was a straightforward matter of putting the appropriate number of rods next to each other and carrying over to the next column when necessary. No memorization was required. However, the multiplication table (the “nine-nines algorithm”) was a different story. It was an important tool, because multiplying 8 × 9 = 72 was faster than adding 8 to itself nine times.
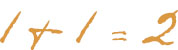
A simple interpretation is this: On the number line, 2 is the number that is one step to the right of 1. However, logicians since the early 1900s have preferred to define the natural numbers in terms of set theory. Then the formula states (roughly) that the disjoint union of any two sets with one element is a set with two elements.
Another exceedingly important notational difference is that not a single ancient culture—Babylonian, Egyptian, Chinese, or any other—possessed a concept of “equation” exactly like our modern concept. Mathematical ideas were written as complete sentences, in ordinary words, or sometimes as procedures. Thus it is hazardous to say that one culture “knew” a certain equation or another did not. Modern-style equations emerged over a period of more than a thousand years. Around 250 AD, Diophantus of Alexandria began to employ one-letter abbreviations, or what mathematical historians call “syncopated” notation, to replace frequent words such as “sum,” “product,” and so on. The idea of using letters such as x and y to denote unknown quantities emerged much later in Europe, around the late 1500s. And the one ingredient found in virtually every equation today—an “equals” sign—did not make its first appearance until 1557. In a book called The Whetstone of Wytte, by Robert Recorde, the author eloquently explains: “And to avoide the tediouse repetition of these woordes: is equal to: I will sette as I doe often in woorke use, a paire of paralleles, or Gemowe lines of one lengthe, thus:  because noe 2 thynges can be moare equalle.” (The archaic word “Gemowe” meant “twin.” Note that Recorde’s equals sign was much longer than ours.)
because noe 2 thynges can be moare equalle.” (The archaic word “Gemowe” meant “twin.” Note that Recorde’s equals sign was much longer than ours.)
So, even though mathematicians had implicitly known for millennia that 1 + 1 = 2, the actual equation was probably not written down in modern notation until sometime in the sixteenth century. And it wasn’t until the nineteenth century that mathematicians questioned our grounds for believing this equation.
THROUGHOUT THE 1800s, mathematicians began to realize that their predecessors had relied too often on hidden assumptions that were not always easy to justify (and were sometimes false). The first chink in the armor of ancient mathematics was the discovery, in the early 1800s, of non-Euclidean geometries (discussed in more detail in a later chapter). If even the great Euclid was guilty of making assumptions that were not incontrovertible, then what part of mathematics could be considered safe?
In the late 1800s, mathematicians of a more philosophical bent, such as Leopold Kronecker, Giuseppe Peano, David Hilbert, and Bertrand Russell, began to scrutinize the foundations of mathematics very seriously. What can we really claim to know for certain, they wondered. Can we find a basic set of postulates for mathematics that can be proven to be self-consistent?
Opposite The key to arithmetic: an Arabic manuscript, by Jamshidal-Kashi, 1390–1450.
Kronecker, a German mathematician, held the opinion that the natural numbers 1, 2, 3, … were God-given. Therefore the laws of arithmetic, such as the equation 1 + 1 = 2, are implicitly reliable. But most logicians disagreed, and saw the integers as a less fundamental concept than sets. What does the statement “one plus one equals two” really mean? Fundamentally, it means that when a set or collection consisting of one object is combined with a different set consisting of one object, the resulting set always has two objects. But to make sense of this, we need to answer a whole new round of questions, such as what we mean by a set, what we know about them and why.
In 1910, the mathematician Alfred North Whitehead and the philosopher Bertrand Russell published a massive and dense three-volume work called Principia Mathematica that was most likely the apotheosis of the attempts to recast arithmetic as a branch of set theory. You would not want to give this book to an eight-year-old to explain why 1 + 1 = 2. After 362 pages of the first volume, Whitehead and Russell finally get to a proposition from which, they say, “it will follow, when arithmetical addition has been defined, that 1 + 1 = 2.” Note that they haven’t actually explained yet what addition is. They don’t get around to that until volume two. The actual theorem “1 + 1 = 2” does not appear until page 86 of the second book. With understated humor, they note, “The above proposition is occasionally useful.”
Below A clay tablet impressed with cuneiform script details an algebraic-geometrical problem, ca. 2000–1600 BC.
It is not the intention here to make fun of Whitehead and Russell, because they were among the first people to grapple with the surprising difficulty of set theory. Russell discovered, for instance, that certain operations with sets are not permissible; for example, it is impossible to define a “set of all sets” because this concept leads to a contradiction. That is the one thing that is never allowed in mathematics: a statement can never be both true and false.

But this leads to another question. Russell and Whitehead took care to avoid the paradox of the “set of all sets,” but can we be absolutely sure that their axioms will not lead us to some other contradiction, yet to be discovered? That question was answered in surprising fashion in 1931, when the German logician Kurt Gödel, making direct reference to Whitehead and Russell, published a paper called “On formally undecidable propositions of Principia Mathematica and related systems.” Gödel proved that any rules for set theory that were strong enough to derive the rules of arithmetic could never be proven consistent. In other words, it remains possible that someone, someday, will produce an absolutely valid proof that 1 + 1 = 3. Not only that, it will forever remain possible; there will never be an absolute guarantee that the arithmetic we use is consistent, as long as we base our arithmetic on set theory.
MATHEMATICIANS DO NOT actually lose sleep over the possibility that arithmetic is inconsistent. One reason is probably that most mathematicians have a strong sense that numbers, as well as the numerous other mathematical constructs we work with, have an objective reality that transcends our human minds. If so, then it is inconceivable that contradictory statements about them could be proved, such as 1 + 1 = 2 and 1 + 1 = 3. Logicians call this the “Platonist” viewpoint.
“The typical working mathematician is a Platonist on weekdays and a formalist on Sundays,” wrote Philip Davis and Reuben Hersh in their 1981 book, The Mathematical Experience. In other words, when we are pinned down we have to admit we cannot be sure that mathematics is free from contradiction. But we do not let that stop us from going about our business.
Another point to add might be that scientists who are not mathematicians are Platonists every day of the week. It would never even occur to them to doubt that 1 + 1 = 2. And they may have the right of it. The best argument for the consistency of arithmetic is that humans have been doing it for 5000 years and we have not found a contradiction yet. The best argument for its objectivity and universality is the fact that arithmetic has crossed cultures and eras more successfully than any other language, religion, or belief system. Indeed, scientists searching for extraterrestrial life often assume that the first messages we would be able to decode from alien worlds would be mathematical—because mathematics is the most universal language there is.
We know that 1 + 1 = 2 (because it can be proved from generally accepted principles of set theory, or else because we are Platonists). But we don’t know that we know it (because we can’t prove that set theory is consistent). That may be the best answer we will ever be able to give to the eight-year-old who asks why.