3

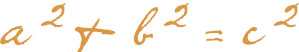
the square of the hypotenuse the pythagorean theorem

For many mathematics students, the first name they encounter in a mathematics course is the name of Pythagoras. The Pythagorean Theorem states that in any right triangle (that is, a triangle containing one right angle) the sum of the squares of the two shorter sides (a and b) equals the square of the longest side (c), called the hypotenuse. The formula, memorized by centuries of students, is a² + b² = c².

The Pythagorean Theorem is famous enough that it has appeared often in popular culture. In the movie The Wizard of Oz, the scarecrow memorably botches the theorem after the wizard awards him a diploma, exclaiming, “The sum of the square roots of any two sides of an isosceles triangle is equal to the square root of the remaining side. Oh, joy, oh, rapture. I’ve got a brain!” In Gilbert and Sullivan’s musical The Pirates of Penzance, the Major General demonstrates a somewhat better command of mathematics when he sings, “I’m very well acquainted, too, with matters mathematical … With many cheerful facts about the square of the hypotenuse.”

Who was Pythagoras, and what did he have to do with the theorem that bears his name? As it turns out, the answer is rather complicated. In all likelihood, Pythagoras neither discovered nor proved “his” theorem. It is long past time for the theorem to be given a more accurate name.

The letters a and b represent the legs (short sides) of a right triangle, and c represents the hypotenuse (long side).

Pythagoras was born around 569 BC on the island of Samos, off the coast of Ionia (modern-day Turkey). According to legend, he spent years absorbing the wisdom of the ancients in Egypt, and perhaps Babylonia, maybe even India for that matter (when you are a legend, all things are possible). After returning home, he then emigrated permanently to the Italian city-state of Croton. There he founded a secret society known as the Pythagoreans, which for a period dominated the cultural and civic life of Croton.

As cults go, the Pythagoreans were only mildly eccentric. Pythagoras preached the virtues of temperance, reverence for one’s elders, and education. He advocated monogamy, which must have come as a shock to a society whose gods were serial adulterers. He forbade the consumption of animal flesh, because an animal might have the soul of a friend or an ancestor. In addition, he prohibited the eating of beans, possibly because human souls could migrate to these plants as well.

All in all, Pythagoras could be seen as a rather typical charismatic leader of a mystery cult. But what distinguishes the Pythagoreans, at least to a historian of science, is their alleged role as the founders of the Greek traditions of mathematics and philosophy. Pythagoras believed that everything in the world was governed by numbers.

Above Right triangles: general (left) and particular (right).

Pythagorean philosophy included a great deal of numerology, or number mysticism, some of which appears laughable to modern eyes. For example, odd numbers were thought to be masculine and even numbers feminine. But their fascination with numbers did lead the Pythagoreans to some concepts that remain quite relevant to the modern subject of number theory. For instance, they discovered what they called “perfect numbers” (numbers that are equal to the sum of all their proper divisors). The first two perfect numbers are 6 (which equals 1 + 2 + 3) and 28 (which equals 1 + 2 + 4 + 7 + 14). At the time of writing, 47 perfect numbers are known, and as computers get faster and faster, they turn up new ones every few years.

AN EVEN MORE FRUITFUL concept was that of prime numbers: that is, numbers that have only themselves and 1 as divisors. The first few primes are 2, 3, 5, 7, and 11. Numbers that are not prime are called composite (for example, 6 is the product of two primes, 2 × 3).

Without prime numbers, number theory would be a relatively barren subject. With them, it is endlessly fascinating. The ancient Greeks proved that the primes never end; however, the details of how they are interspersed among the integers remain very mysterious. Primes can be used both to solve whole-number equations and to show they are unsolvable; Fermat’s Last Theorem is but one example, as will be discussed in a later chapter. And finally, primes are essential for modern-day cryptography, much of which is based on the idea that it is hard to find the prime factors of a very large composite number—say, one with a few hundred digits.

Among the other mathematical discoveries attributed to the Pythagoreans were the Pythagorean theorem, and perhaps more importantly, a proof of the Pythagorean theorem; the principle that musical chords are formed by vibrations whose frequencies form simple whole-number ratios (for instance, an octave is created by the ratio 2:1, a fifth is created by the ratio 3:2, and a fourth is created by the ratio 4:3); the belief that the motions of the planets were governed by similar integer ratios—according to legend, Pythagoras could actually hear the harmonies that the planets produced, known as “the music of the spheres”; and finally the existence of irrational numbers.

Do these claims hold water?

First, one of the few things that can be stated with absolute certainty about Pythagoras is that he did not discover the Pythagorean theorem. A famous Babylonian tablet known as Plimpton 322, dating to roughly 1800 BC, contains a list of what we would now call Pythagorean triples: sets of integers (such as 3–4–5 or 5–12–13) that form the sides of a right triangle. (As you can readily check, 3² + 4² = 5² and 5² + 12² = 13².) As Pythagoras supposedly studied in Babylonia, one may surmise that he learned the Pythagorean formula there.

Above right Pythagorean Theorem described in an early Arab book.

It would be much more interesting if Pythagoras actually discovered a proof of the Pythagorean theorem, in other words a demonstration from elementary principles that the formula a² + b² = c² holds for all right triangles. The Babylonians and Egyptians were apparently not interested in such mathematical deductions; their extant texts are long on procedures and short on explanations. (An explanation, for the Babylonians, is “Behold, it is done,” followed by “Praise Nisaba.”)

In the two centuries that followed Pythagoras, ancient Greece did develop a rich tradition of deductive mathematics, unprecedented in world mathematics. It culminated in Euclid’s Elements, written around 300 BC. The first book of the Elements includes a careful proof of the Pythagorean theorem. It would be amazing, and wonderful, if the proof could be traced to the very beginning of ancient Greek mathematics.

ONCE YOU HAVE ACCEPTED, or proved, that the equation a² + b² = c² holds for every right triangle (and not just for convenient ones like 3–4–5 or 5–12–13), you run straight into a conundrum. The simplest right triangle of all is the one created by cutting a square in two parts along the diagonal. This triangle has two legs of equal length, which can be assumed to be 1 unit and 1 unit. Then, according to the Pythagorean theorem, the length of the hypotenuse, c units, obeys the equation c² = 2.

But according to Pythagorean dogma, everything in the universe is supposed to be governed by whole numbers. So this mysterious length c should be expressible as a ratio of integers, say p/q. It’s easy to find some “close calls.” For example 7/5 is just a little too small, because (7/5)² = 49/25 = 1.96, and 17/12 is just a little too big, because (17/12)² = 289/144 ≈ 2.007. Thus you can say that length c is between 7/5 and 17/12 … But try as you might, you won’t be able to find whole numbers p and q such that (p/q)² = 2.

You may wonder how I can be so sure. Let’s assume that you could find a ratio p/q whose square is 2. Then p² = 2q², so p² is an even number. Thus p is even, and so there is some whole number x such that p = 2x. Thus 4x² = (2x)² = p² = 2q², so q² = 2x². Thus q is also an even number, and expressible as q = 2y. But then p/q = x/y, which means we have found smaller numbers x and y with the same ratio. But then we could apply the same argument to x and y, getting a ratio with even smaller numbers. And so the process would never end—we could never reduce the fraction to its lowest terms! This is an absurdity, and therefore the assumption that (p/q)² = 2 must have been fallacious. This kind of proof is called a reductio ad absurdum, or proof by contradiction, and will be discussed further in Chapter 5.

Nowadays, we have other ways of expressing the length of the hypotenuse, c. A standard 10-digit pocket calculator says that the length is 1.414213562. But the Pythagoreans did not have a decimal notation system—decimals would not come to Europe for another 1500 years! So they did not have the option of writing the answer this way. And anyway, 1.414213562 is still not the exact length. The square of this number is 1.999999998, not 2.

A second way around this conundrum is to write c = √2. This is what is taught in school. The answer looks comfortingly exact … but it is also vacuous. It says that the number whose square is 2 is … the square root of 2. It tells us nothing that we didn’t already know!

In any event, the Pythagoreans lacked the √ notation, and surely would not have been satisfied by such a self-referential answer. So they literally had no way of writing down the length of the diagonal of a square. It was alogos, a concept that could not be expressed in words. Today we would say that it is an irrational number. (A rational number is one that can be written as a ratio of whole numbers, such as 7/5.) If the term “irrational” sounds a bit pejorative, that is no accident. For the Pythagoreans, if a number could not be expressed in words, it should not be expressed in words. The existence of alogos numbers should be kept as a mystery only for the deepest initiates. Legend has it that the first person who revealed the secret (possibly a Pythagorean named Hippasus) was drowned at sea as punishment.

This is a marvelous tale, but it is probably not true. It is unlikely that Pythagoras could have proved that the number √2 is alogos. The “proof by contradiction” technique, which lies at the heart of the argument, was introduced two generations after Pythagoras, by Zeno of Elea (a student of Parmenides, who is sometimes described as a Pythagorean but was not actually a member of the society).

Nowadays, historians place much less stock than they once did in the alleged accomplishments of Pythagoras and the Pythagoreans. There simply is no documentary evidence of it, while there is a great deal of evidence about the accomplishments of ancient Greek mathematicians who were not in the brotherhood. For instance, Theodorus of Cyrene, who also was not a Pythagorean, proved around 400 BC that the numbers we would call √3, √5, and so on up to √17 were also irrational. (The fact that he began with √3 suggests that the irrationality of √2 was already accepted by this time.)

From the viewpoint of modern historians, it makes more sense to study the many documented advances of ancient Greek mathematicians who were not Pythagoreans, than to perpetuate unsubstantiated legends about the Pythagoreans. One modern historian, M.F. Burnyeat, argues that the legend of Pythagoras was deliberately fabricated by Plato’s successors in order to portray Plato as the heir to an ancient tradition.

Opposite Allegory of Arithmetic (1504) by Gregor Reisch, showing Pythagoras using an abacus on the right, while the Roman philosopher Ancius Boethius uses Arabic numerals and mathematical symbols.

There is one more good reason not to canonize Pythagoras. Science progresses much more rapidly when it is communicated openly than when it is shrouded in secrecy. As long as mathematics was hidden behind the veil of secrecy, it was impossible to separate genuine mathematics from bogus numerology. Once mathematics came out from behind the Pythagorean veil, the way was opened to new discoveries, such as those of Theodorus (and Eudoxus, Eratosthenes, Euclid, Archimedes, …). If we are celebrating ancient Greek mathematics, we should give most of the credit not to the secret cult of Pythagoras, but to the spirit of open inquiry that followed after its dispersal.

It seems a shame, also, to attribute the Pythagorean theorem to one person, when it is one of the great universal theorems of mathematics. The Pythagorean formula was discovered independently, it seems, by nearly every ancient culture. In some sense, it seems to be an inevitable discovery for any mathematically inclined civilization. If “God created the integers,” as Kronecker said, perhaps he created the Pythagorean theorem too.

IN CHINA, for instance, the Pythagorean formula was known as the gou-gu rule. In Chinese terminology, gou (leg) was the shorter side of a right triangle, and gu (thigh) was the longer side. (Compare this to the Western terminology where both sides are simply called legs.) The hypotenuse was called xian, or “lute string,” which may allude to the origins of the theorem in measuring distances with a stretched rope.

The gou-gu rule appears in the anonymously written Jiu Zhang Suan Shu, or Nine Chapters on the Art of Mathematics, a seminal work for Chinese mathematics that was as influential as Euclid’s Elements in the West. The age of the Nine Chapters is unknown. Liu Hui, a commentator in the third century AD, strongly implies in his preface that the Nine Chapters existed before the Chinese emperor Qin Shi Huang ordered all books to be burned, in 213 BC. After Qin’s death, the Nine Chapters had to be reconstructed from memory. It is easy to imagine how imperfect this process was. Thus, as the work was passed down from generation to generation, a long tradition arose of improvements and comments on the original text.

Liu Hui’s annotation of the Nine Chapters was one of the best, and contains much material of his own. Liu, a self-taught mathematician, may perhaps be considered the first Chinese math geek; he studied the subject because he cared about it and not because it would advance his career in court. In his annotations we find many explanations of why the statements in the Nine Chapters are true, and in particular we find the first documented proof of the Pythagorean theorem outside of ancient Greece.

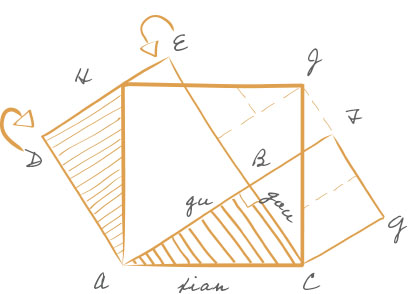
Liu’s argument is reminiscent of the equally ancient Chinese puzzle of tangrams, in which a small set of simple pieces is rearranged to produce a fantastic variety of figures. He starts with two squares made from the sides of the gou and the gu, and then dissects them and rearranges the pieces so that they form a square on the xian. This kind of proof, called the “out-in” method, was used repeatedly by Liu and by other Chinese mathematicians. It is a much simpler proof to understand than the one in Euclid’s Elements.

Below The gou-gu theorem. Liu Hui’s proof shows that the squares on the gu and the gou (ABED and BCGF) can be cut into smaller pieces and rearranged to form the square on the xian (ACJH).

IN ONE RESPECT, the history of the gou-gu theorem in China diverges dramatically from its counterpart in ancient Greece. As we have seen, in ancient Greece the Pythagorean theorem led to the discovery of irrational numbers, such as √2. Chinese mathematicians, on the other hand, never explicitly formulated the concept of irrationality. Some historians have attributed the different paths of Chinese and Greek mathematics to the greater “practicality” of the former, and have suggested that the Chinese were not so interested in abstract reasoning. However, Liu Hui had no aversion to abstract reasoning or to the “impractical” side of mathematics. Joseph Dauben, a leading historian of Chinese mathematics, believes that the explanation lies in the Chinese language itself, in which it is difficult to express a counter-factual assumption. Recall that the proof of irrationality of √2 begins with the counter-factual sentence, “Let’s assume that you could find a ratio p/q whose square is 2.” Presumably, an ancient Chinese mathematician would simply not have been able to make sense of this first step. How can a false assertion be used to justify a true theorem?

Such differences are, once again, a reminder that there is no unique correct approach to mathematics. Even in the twentieth century, a school of mathematics called constructivism maintained that proofs by contradiction should not be allowed. They would find the argument above for the irrationality of √2 to be completely unconvincing. Like the ancient Chinese, they would be more interested in the fact that √2 is computable. (In other words, there is a well-defined procedure for approximating it to any desired degree of precision.) The more things change, the more they stay the same.