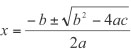
the stammerer’s secret cardano’s formula
The story of Cardano’s formula really begins more than 3000 years earlier. In the period between 1850 and 1650 BC, problems like this one proliferated in Babylonian mathematical tablets: find two numbers whose product is 60, and whose difference is 7. A modern mathematician would call the numbers x and y and note that y = 60/x. Therefore, x – 60/x = 7, or equivalently, x2 – 7x – 60 = 0. Then one would trot out the quadratic formula, which says that the solution to any quadratic equation, ax2 + bx + c = 0, is given by:
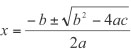
Using a = 1, b = –7, and c = –60, said mathematician would obtain the solutions x = 12 and y = 60/12 = 5.
However, the Babylonians did not have the algebraic tools that we do today. Instead, the scribe took a more intuitive approach, which involved drawing a rectangle with the unknown side lengths, x and y, cutting it into pieces, and rearranging the pieces into an L-shaped figure, as shown on page 62. He then “completed” the L-shaped figure by adding a small square of known area in the corner. A similar method of solution—called “completing the square”—is still taught in high-school algebra as a precursor to the quadratic formula, but usually with no reference to its geometric meaning or its historical provenance.
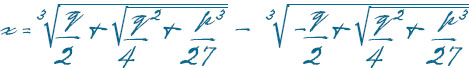
Cardano’s formula for solving a reduced cubic polynomial, x3 + px = q
The other ancient mathematical cultures also “knew” the quadratic formula or else had equivalent methods for solving quadratic equations. Euclid employed a geometrical construction that produced a line segment of the requisite length. In seventh-century India, Brahmagupta, discussed previously in relation to zero, provided a recipe to solve the equation ax2 + by = c that is essentially the quadratic formula written in words instead of symbols.
However, classical mathematics is essentially silent* on the question of how to solve a cubic equation, ax3 + bx2 + cx + d = 0. In 1494, Fra Luca Pacioli, an Italian mathematician, expressed the opinion that cubic equations would never be solved exactly. Pacioli was proved wrong only a generation later!
Left “Completing the square.”
In the early 1500s, a Bolognese mathematician named Scipio del Ferro apparently found a method for solving cubic equations that are lacking the quadratic term: in other words, any equation of the form x3 + px = q. Nowadays, a mathematician who made such a discovery would hasten to publish it. However, in the Italy of that era, mathematicians made their reputations by defeating other mathematicians in problem competitions. Del Ferro therefore kept his method secret, so that he could pose problems that his opponents would not be able to solve. Only on his deathbed did he confide his secret to two of his students, Antonio Maria Fiore and Annibale della Nave.
However, rumors soon spread about del Ferro’s discovery. In the early 1530s, Tartaglia started claiming that he, too, could solve cubic equations. Thinking he could call Tartaglia’s bluff, Fiore rashly challenged Tartaglia to a competition. According to the legend (which is probably a little too good to be true), on the eve of the debate Tartaglia finally figured out how to solve these cubics, and so he thoroughly trounced Fiore.
How, then, did Cardano get his name on what should have become known as Tartaglia’s or del Ferro’s formula? It becomes a little less surprising when you read Girolamo Cardano’s own description of himself: He wrote in his autobiography that he was “hot tempered, single minded, and given to women … cunning, crafty, sarcastic, diligent, impertinent, sad and treacherous, miserable, hateful, lascivious, obscene, lying, obsequious …” He had studied to become a physician at the University of Padua, but perhaps because of his erratic behavior he was forbidden to practice medicine in Milan until 1539. However, even before then he found great success as a public lecturer and writer on a variety of topics, including mathematics.
In 1539 Cardano was composing a mathematical handbook called Practica arithmeticae generalis, and he asked Tartaglia for the secret to solving cubic equations. Tartaglia at first refused, on the grounds that he intended to write a book of his own. But at last, Cardano persuaded Tartaglia to come to his house for a visit. On the night of March 25, 1539, Tartaglia revealed his method under an oath of strict secrecy.
And here is the secret, in an English translation by math historian Jacqueline Stedall. (Tartaglia’s version, in Italian, actually rhymes!) For ease of understanding, Tartaglia’s verse has been interpreted here in algebraic symbols. “The thing” means the unknown quantity x, “the cube” means x3, and “the number of things” is p. The equation Tartaglia wants to solve is x3 + px = q, and the numbers p and q are positive. (This last point is irrelevant to mathematicians today, but was very relevant to sixteenth-century Italians, who were still as skeptical of negative numbers as the nineteenth-century-BC Babylonians.)
Tartaglia |
Algebra |
When the cube with the things next after |
When x3 + px |
Together equal some number apart |
= q, |
And this you will then keep as a rule |
|
That their product will always be equal |
And such that uv = |
To a third cubed of the number of things |
|
The difference then in general between |
Then |
The sides of the cubes subtracted well |
|
Will be your principal thing. |
= x |
Tartaglia’s formula is a well-disguised way of “completing the cube,” but it includes a very clever new step that was not present in the Babylonian process of completing the square: the introduction of two new auxiliary variables, u and v. Here is how it works for an example considered later by Cardano: x3 + 6x = 20. Tartaglia instructs us to find two numbers u and v such that uv = (6/3)3 = 8 and u – v = 20. This pair of equations can be solved by the quadratic formula: u = 10 + 6√3 and v = –10 + 6√3. (These are the two positive solutions.) Now we are supposed to find the cube roots of u and v. In general one would have to do this by approximation, either by hand or with an abacus. But in this particular case the cube roots have a simple exact form:
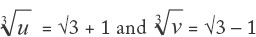
Below An engraving from frontispiece of Cardano’s work Ars Magna, 1545, the first great Latin book dedicated to algebra.
Finally, we subtract these to get the answer: x = (√3 + 1) – (√3 – 1) = 2
AT FIRST, Cardano honored his pledge not to publish Tartaglia’s method. However, over the next few years several things happened that made him itch to see the solution in print. First, he and his protégé, Ferrari, went beyond Tartaglia, by showing how to simplify any cubic equation to del Ferro’s form or one of 12 other basic forms. Second, Ferrari “invented at my request” (as Cardano later wrote) a method for solving quartic or fourth-degree equations. This latter discovery is far more remarkable than Cardano’s offhand comment would suggest. More than 3000 years elapsed between the solution of the quadratic and the first solution of the cubic—but it took Ferrari only four years to move on to quartics! Unfortunately, the solution to the cubic was an intermediate step in the solution of quartics. The promise to Tartaglia was now a major obstacle: Without the method for solving cubics, Cardano could not publish Ferrari’s brilliant solution for quartics.

At this point Cardano found an ingenious loophole. In 1543, he tracked down del Ferro’s other student, della Nave in Bologna, and ascertained that Tartaglia’s method for solving the cubic was exactly the same as del Ferro’s. This fact apparently released Cardano (at least, in his own mind) from his promise to Tartaglia to keep it a secret. Two years later, Cardano published his greatest mathematical work, Ars magna (The great art), with a complete treatment of cubics and quartics, and the secret was out.
Tartaglia, of course, felt that Cardano had betrayed him. He fired off a volley of insulting open letters, as well as a book of his own. Cardano, however, remained above the fray and allowed Ferrari to do the answering for him—a task that Ferrari took to with great zest, and ultimately with the successful outcome recounted at the beginning of this chapter.
It may seem unjust that the formula for solving the cubic is now known as Cardano’s formula—not del Ferro’s, or Tartaglia’s, or even Ferrari’s. But as has already been stated in the last chapter, mathematics thrives when it is communicated openly. It is not enough merely to discover America—you must make the discovery known to the rest of the world. Cardano alone took that final step, and reaped the glory.
CARDANO’S FORMULA had a lasting impact that far exceeded the importance of the problem it solved. For example, it provided one of the first motivations for the use of imaginary numbers and complex numbers in mathematics. Imaginary numbers are numbers whose square is negative (a property no real number has). Using imaginary numbers, we can say that –1 has two square roots, which are denoted by i and –i. Without imaginary numbers, we would have to say that –1 has no square roots. Once we have imaginary numbers, we can define complex numbers as numbers that have both a real and an imaginary part, such as 1 + 2i.
Not only modern-day mathematics but also modern-day physics would be unthinkable without imaginary numbers. In quantum mechanics, for instance, elementary particles such as photons are defined to be “wave functions.” The wave function for a photon at some point will in general have complex-number values, such as 0.2 + 0.3i. The imaginary part of the wave function accounts for the wavelike properties, or “phase,” of the photon; for instance, it explains why a light beam that shines through two slits forms a diffraction pattern on the other side, rather than two bright bars (see Young’s experiment, on page 143). Thus, imaginary numbers seem to be woven in a very real way into the fabric of the universe.

Above A title page vignette illustrated in Cardano’s Opera omnia, 1663, depicting Ptolemy and Euclid.
Prior to Cardano, it did not occur to anybody to assert that –1 has two square roots but they are imaginary. You might compare it to asking a child how many imaginary friends she is inviting to her birthday party. But in the case of cubic polynomials, these “imaginary friends” actually left behind some real birthday presents! In 1572, Rafael Bombelli presented an example of this phenomenon. The equation x3 = 15x + 4 has a real solution, x = 4, that can be verified by substitution. However, Cardano’s formula gives:
Cardano had no interest in such nonsense: “So progresses arithmetic subtlety, the end of which, as is said, is as refined as it is useless,” he once wrote. But Bombelli realized that these expressions have meaning. The first cube root is equal to 2 + i and the second is equal to 2 – i, and therefore x = (2 + i) + (2 – i) = 4. In the final solution the imaginary quantities have disappeared, but we could not have gotten to the solution without them.
Thankfully, today’s students are no longer expected to learn Cardano’s formula. Nevertheless, nineteenth-century students were expected to know how to solve cubics. Albert Einstein, in his university exams, correctly solved a problem with Cardano’s formula—in contrast to the surprisingly persistent legend that he was a poor mathematics student.
Another long-delayed ramification of Cardano’s formula involved the solution of higher-degree equations. After the cubic and quartic had been tamed, one might have expected the solution of fifth-degree polynomials, or quintics, to follow shortly thereafter. But strangely, another 250 years went by with very little progress. Some quintic equations can be solved. But no universal solution, applicable to all quintics, was ever found.
In 1824, a Norwegian mathematician named Niels Henrik Abel finally showed that there could not be any Cardano-like formula for the solutions to a fifth-degree equation. (“Cardano-like formula” refers to any formula that involves square roots, cube roots, fourth roots, etc., possibly nested inside one another. Mathematicians call this a “solution by radicals.”) Abel’s theorem may have closed one chapter of mathematics, but it opened another. His proof led mathematicians to a deeper understanding of the concept of symmetry, a topic to be discussed in chapter 14.
* An exception is the Persian poet and mathematician Omar Khayyam (1050–1130), who showed how to solve a large class of cubic equations by geometrical constructions (e.g., by finding the intersection point of a parabola and a circle). However, the results are not readily convertible into numerical form, and are not equivalent to the later work of Tartaglia and Cardano.