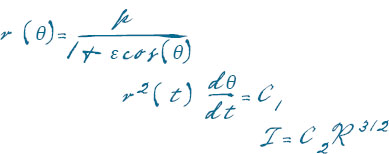
order in the heavens kepler’s laws of planetary motion
Another great battle of sixteenth- and seventeenth-century science was fought over a “revolutionary” theory that actually was not a revolution. In 1543, while on his deathbed, Nicolaus Copernicus published a book called De revolutionibus orbium coelestium, which placed the Sun, not Earth, at the center of the solar system. Although Copernicus’ theory was at odds with the ecclesiastical understanding of the cosmos, it was definitely not a new idea. Aristarchus of Samos, a Greek philosopher, had already discussed a heliocentric model of the universe in the fourth century BC.
In the early years of the 1600s, two events thrust the “Copernican” (but really Aristarchan) theory into the center of a storm of controversy. The first was the invention of the telescope in 1608. Secondly, using one of these new instruments, Galileo Galilei discovered four small moons orbiting Jupiter. For Galileo, and for anyone else who took the trouble to look through the telescope, here was direct visual evidence of objects in the universe that did not orbit Earth. Galileo’s discovery sounded the death knell for the dogma that Earth was the center of the universe.
It is easy to paint Galileo as the great champion of the Copernican theory, and indeed his story is full of drama and martyrdom. Brought to trial by the Inquisition in 1633 on a charge of heresy for advocating the view that the Earth was not the center of the universe, Galileo was convicted, forced to recant, and confined to house arrest for the rest of his life. However, there is a second hero of the story who is not quite as well known, yet perhaps deserves equal credit: Johannes Kepler.
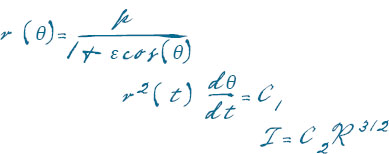
The function r(θ) represents the distance of a planet from the Sun when its location on the zodiac is θ degrees. The angular position θ(t) is itself a function of time, t. The total time it takes the planet to go around the Sun is T. The constants p and R describe (roughly) the width and length of the orbit. The eccentricity, ε, describes how far the orbit deviates from a perfect circle. C1 and C2 are two empirical constants.
Although he is primarily considered an astronomer, Kepler had a real gift for mathematics and for bold conjecture. He was able to spot patterns where no one else had before—and sometimes where none existed. For example, when Galileo announced his discovery that Jupiter had four moons, Kepler conjectured that Mars must have two moons and Saturn eight, in order to make a geometrical progression: 1 (Earth), 2 (Mars), 4 (Jupiter), 8 (Saturn). Amazingly, he was right about Mars, but the “pattern” was an utter coincidence. Jupiter has 63 moons that we know about, and Saturn has 62.
It is easy to understand why Kepler, with his speculative temperament, was one of the first scientists to wholeheartedly embrace Copernicus’ theory. It is a bit more of a surprise to see him chastising Galileo for not doing the same. In 1597, when Galileo wrote to him that he agreed with Copernicus but dared not publish his opinion, Kepler wrote back: “I would have wished, however, that you, possessed of such an excellent mind, took up a different position … Have faith, Galilei, and come forward!” Nevertheless, Galileo remained publicly silent for thirteen more years, until his discovery of the Galilean moons of Jupiter gave him the evidence he needed to “come forward.”
NOWADAYS, KEPLER’S FAME rests on three mathematical laws that he discovered by analyzing the painstaking observations of the orbits of the planets that had been taken by his former employer, the Danish astronomer Tycho Brahe. His laws form a bridge from the old style of astronomy, which was concerned with describing the cosmos, to a new style that explains the motions of the planets and other celestial bodies. They are still descriptive laws, but they are so precise that they virtually beg for a mathematical proof. Isaac Newton provided the proof in 1686, roughly three-quarters of a century later.
Kepler’s first law states that planets orbit the Sun in ellipses, not circles, with the Sun at one focus. To express this in equation form, we could write it as follows:
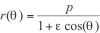
Here r(θ) represents the distance from the planet to the Sun when it is θ degrees away from aphelion (its greatest distance from the Sun). The number p represents the distance when the planet is 90 degrees away from aphelion, and the number ε represents the eccentricity, or departure from circularity, of the planet’s orbit. Notice that if the eccentricity ε is zero, the equation becomes r(θ) = p: in other words, the distance from the planet to the Sun is a constant. In this case, and only in this case, the orbit is a circle.
Ironically, Kepler’s first law was actually a departure from strict Copernicanism. The Sun is not at the center of Earth’s orbit, but slightly displaced from it. At its closest approach to the Sun, called perihelion, Earth is about 91.3 million miles (147 million kilometers) away. At its greatest distance, Earth is 94.5 million miles (152 million kilometers) away. More importantly, Kepler’s law made a clean break with centuries of tradition that tried to describe planetary orbits either as circles, or as complicated combinations of circular motions. Aristotle had considered circles to be the most perfect curves, and therefore the only ones that could describe the motion of the heavenly bodies. In the third century, Ptolemy had refined Aristotle’s system with a complicated, Rube Goldberg-esque arrangement of circular motions superimposed on other circular motions—but even so he could not predict the planets’ motions very accurately. Kepler’s law (to modern eyes) is simple, economical, and far more beautiful than Plutarch’s theory. To determine the shape of any planet’s orbit, you need to know only two numbers: p and ε.
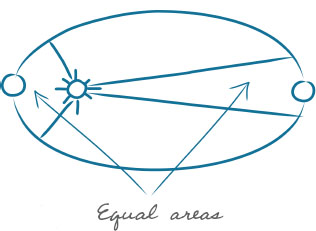
Left Kepler’s Second Law: The line joining a planet and the Sun sweeps out equal areas during equal intervals of time.
But Kepler wasn’t finished. He discovered two more patterns in Brahe’s planetary data that have since been elevated to the status of “laws.” Kepler’s second law states that planets speed up when they get closer to the Sun, and they do so in a precisely quantifiable way. The area that a planet sweeps out in any given, fixed-time interval is the same no matter where the planet is in its orbit. Because Earth is closer to the Sun at perihelion, it must sweep out a fatter triangle in one day at perihelion than it does when it is at aphelion, as shown above.
Earth’s orbit is so nearly circular (ε = 0.0167), that most of us are not aware of these subtle differences. Nevertheless, they do affect us, more profoundly than most people realize. At present, Earth’s closest approach to the Sun falls during the northern hemisphere’s winter. This means that the northern hemisphere has somewhat shorter (and milder) winters than it would if the perihelion came in summertime. However, this will not always be the case. In about 13,000 years, the situation will be reversed, and we will experience longer and more severe winters. The existence of orbital variations like these has been proposed as a contributor to ice ages.
While Kepler’s first two laws were the culmination of an eight-year struggle to understand Brahe’s data on the orbit of Mars, Kepler’s third law seems to have occurred to him quite suddenly—on March 8, 1618, as he was putting the finishing touches to a book called Harmony of the World. Unlike the first two laws, which describe the motion of an individual planet, the third law provides a basis for comparison between planets. It says that the length of a planet’s year is proportionate to the 3/2 power of its distance to the Sun. (Another way of saying this is that the square of the orbital period is proportional to the cube of the mean distance from the Sun.) For instance, Pluto is 39.5 times farther from the Sun than Earth is. Thus it takes (39.5)3/2 = 39.5 √39.5 = 248 years to orbit the Sun.
Opposite The orbit of Mars, an engraving from Astronomia nova by Kepler (1571–1630).
Kepler’s third law is actually more useful in reverse. It is easy to measure the orbital time of a planet around the Sun, or a moon around a planet, or two stars around each other. The hard part is measuring the distance between them. Kepler’s law gives us an immediate way of converting orbital periods to distances. Later improvements, using Newton’s law of gravitation, enable us to infer the mass of moons, planets, or stars from their orbital periods. Such calculations are essential, for instance, in the search for extrasolar planets (i.e., planets in other solar systems) that might be capable of supporting life. If we didn’t know how big and how far away from its sun a planet is, we would not know whether it is habitable. If, one day, we do find evidence of life on a distant planet, we will owe it to Kepler and his third law.