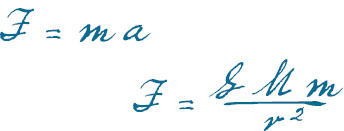
of apples, legends … and comets newton’s laws
Ask most people what they know about Isaac Newton, and there is a good chance that they will tell you about an apple falling from a tree. According to legend, Newton was inspired to formulate his universal law of gravitational attraction by witnessing the fall of an apple, and realizing that the same force that explained its motion could also explain the motion of the planets. In some more recent embellishments, perhaps Newton was inspired by being hit on the head by the apple.
Here is an equally unverifiable counterlegend, which first appeared in print in 1858, in a delightful English journal called Notes & Queries. According to a contributor named “W.”, Karl Friedrich Gauss—the leading mathematician of the day—dismissed the legend as follows: “The history of the apple is too absurd. Undoubtedly, the occurrence was something of this sort. There comes to Newton a stupid importunate man, who asks him how he hit upon his great discovery. When Newton had convinced himself what a noodle he had to do with, and wanted to get rid of the man, he told him that an apple fell on his nose; and this made the matter quite clear to the man, and he went away satisfied.”
What is one to make of such legends? In reality, there is more substance to the apple story than Gauss realized (if the quote from him is authentic). The story is attested by two sources, one of whom was the famous French writer Voltaire, who heard it personally from Newton’s niece. Hardly the sort of “stupid importunate man” that Gauss envisioned! One might think of the story as a highly encoded version of what actually happened. If you do not know the code, then you end up with the cartoonish story that Gauss so vigorously objected to.
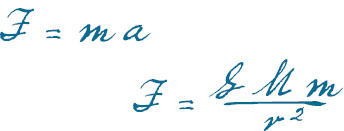
The first equation is Newton’s Second Law of Motion, the second is Newton’s Law of Universal Gravitation. In both equations, F represents a force. The symbol a represents the acceleration of an object with mass m. In the law of universal gravitation, F is specifically the gravitational force between masses m and M, while r represents the distance between the objects. G is the universal gravitational constant, 6.672 × 10-8 cm3 g-1 sec-2.
Was there an apple tree? Yes. It was located at Isaac Newton’s homestead in Woolsthorpe, England. He had lived there until 1661, when he went to Trinity College at Cambridge, and most importantly he returned there in 1665, when the last major outbreak of plague struck England. For close to two years Newton remained in his rural sanctuary. Those were the two years during which he developed the basics of calculus and began thinking about planetary motions. Newton wrote, “In those days I was in the prime of my age for invention and minded Mathematics and Philosophy more than at any time since.”
However, Newton did not need the fall of an apple for inspiration. Gauss was right about that. Newton was surely inspired by the problem itself, which already had centuries of history behind it. Did the Moon, the Sun, and the planets require some sort of external agency to make them move? If so, what was it? Aristotle had argued that heavenly bodies were made of different stuff than Earth, and that their natural motion was circular. Kepler thought that a propulsive force was needed to keep the planets in their orbits. Descartes more or less agreed; in his elaborate theory, the universe was composed of vortices that swept the planets along in their orbits. It is only natural that Newton, as a young scholar, would have been passionately interested in one of the leading scientific debates of the day. He worked out a system in which apples are subject to the same forces as planets. (This is why the apple is important! It refutes Aristotle.) And remarkably, the planets are in free fall at all times; they require no propulsion. (This refutes Descartes and Kepler.)
Opposite The first reflecting telescope, made by Issac Newton in 1668, stands by his manuscript of Principia Mathematica.
While the apple story has some merit, it fails to explain how Newton convinced the rest of the scientific world that his theory was correct. His masterpiece, The Mathematical Principles of Natural Philosophy (often called the Principia after its Latin title), set out to do for physics exactly what Euclid had done for geometry. At the very outset Newton stated three axioms: three laws of motion that all material objects obey, whether they be apples or moons. Later he added the law of universal gravitation, which quantifies how objects attract one another through gravity. From these principles alone, he proved that planets orbiting the Sun obey Kepler’s three laws.
In fact, Kepler’s first law is probably the main reason Newton wrote the Principia. Several other physicists—notably Newton’s rival Robert Hooke, the architect Christopher Wren, and the Dutch physicist Christian Huygens—had also arrived at “Newton’s” law of universal gravitation by the early 1680s. But they had been unable to show that the law causes planets to orbit in ellipses; they could only account for the mathematically much simpler case of circular orbits. In 1684, Newton’s friend Edmund Halley asked Newton if he could prove that planets had elliptical orbits. Newton said that he could, and Halley cajoled him into putting his argument into print. The result, three years later, was much more than the solution of one problem; it was the blueprint for all future physics books.
Halley, who paid for part of the printing costs out of his own pocket, was eventually rewarded for his efforts in a very unique way. Newton’s theory applies to comets, as well as to apples and planets. (In fact, Newton himself emphasized this point.) Because comets follow elliptical orbits, they must return over and over again. Halley realized that one comet in particular had been seen repeatedly at roughly 75-year-intervals: in 1456, 1531, 1606, and 1682. Thus he predicted, correctly, that it would return in 1758 (long after his own death). It has continued to return every 75 to 76 years ever since then, and is now known as Halley’s Comet.
NEWTON’S FIRST LAW states that a moving object will continue moving in a straight line forever, unless some external force stops it or changes its path. This seems quite surprising at first: after all, golf balls don’t keep going forever, and planets don’t move in straight lines. In both cases, the reason is that there are external forces acting on the object. In the case of the golf ball, the forces are gravity, wind resistance (while the ball is in the air), and friction with the ground after it lands. In the case of planets, the hidden force is the Sun’s gravity.
Newton’s second law says that the force on an object equals the rate of change of its momentum. In the language of calculus, we would say that:
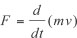
recalling that d/dt denotes the rate of change and mv (where m is the mass of the object and v is its velocity) denotes the momentum. In most applications the mass of the object does not change, and in this case Newton’s second law becomes F = ma (i.e., force equals mass times acceleration), a formula that is today memorized by every beginning physics student.
Newton’s third law, “for every action there is an equal and opposite reaction,” is somewhat less often used by physicists than the first two, but it explains, for example, why a rocket works. The action of propelling exhaust out of the rocket’s nozzles creates a reaction: the acceleration of the rocket in the opposite direction.
Collectively, these three laws explain how all forces affect the motion of all solid bodies. On the other hand, Newton’s law of gravitation pertains to one force only, the force of gravity. It states that the gravitational attraction between any two objects, one of mass M and the other of mass m, is:
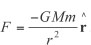
The denominator r2 indicates that the strength of the gravitational force is inversely proportional to the square of the planet’s distance (r) from the Sun. (This is the part of the formula that Hooke, Wren, and Huygens had already guessed.) The minus sign and the vector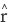 
(read as “r-hat”) indicates that the direction of the force is toward the Sun. In other words, Kepler and Descartes were wrong. There is no force pushing the planets forward in their orbits, only a gravitational force pulling them to the side (that is, toward the Sun).
Newton’s truly novel accomplishment was his ability, using calculus,‡ to combine the law of gravitation with his laws of motion to set up—and then solve—equations describing a planet’s orbit. Together, his physical insight and his mathematical tools ushered in a new era of celestial dynamics, when the motion of planets—and eventually, rockets and spacecraft—could be predicted and controlled, rather than merely observed.
‡ It is often claimed that Newton deliberately avoided the use of calculus in the Principia, rewriting all the proofs in terms of Euclidean geometry. It is true that he avoids the notation of calculus, but his work is fully imbued with the ideas of calculus.
