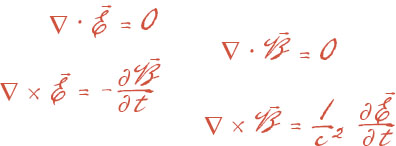
a god’s-eye view of light maxwell’s equations
While mathematics was experiencing revolutions in algebra, geometry, and the theory of functions, physics was undergoing its own revolution.
At the beginning of the nineteenth century, the theories of mechanics and gravity were in pretty good shape. Newton had explained how planets orbit around the Sun. Euler, Laplace, and others had explained multiple-body interactions in the solar system, such as the precession of the equinoxes and the slow variations in Jupiter and Saturn’s orbits. Newton’s laws had explained how solid objects respond to mechanical forces, and Euler’s equations of hydrodynamics had done the same thing for fluids.
However, three subjects in physics remained entirely mysterious to the scientific community: electricity, magnetism, and the nature of light. As of 1800, there was not the slightest bit of evidence that any of these three phenomena were related to the others. Yet by 1865, that had all changed and physicists had arrived at a theory that unifies all three subjects. Magnetic fields are produced by electric currents. Electric fields are generated by changing magnetic fields. And light is nothing more than a traveling electromagnetic wave—an intricately woven tapestry of vibrating magnetic fields and electric fields that cross one another like the warp and the weft of a piece of fabric.
E and B represent the electric and magnetic fields in a vacuum, with no electric charges or currents present. The constant c is the speed of light. The symbol “∇” (the divergence) represents the tendency for field lines to move apart. The symbol “∇ ×” (the curl) represents the tendency of the field lines to rotate. Collectively, the equations say that in the absence of electric charges, neither the electric field nor the magnetic field has any sources or sinks.
In order to reach these conclusions, physicists first had to assimilate a number of startling experimental discoveries. Then they had to develop a new kind of physics, in which solid, tangible objects (like wheels, bars, pulleys, and levers—the stuff of mechanics) were replaced by intangible concepts such as electric and magnetic fields. Because common sense and everyday experience no longer apply to these intangible but real phenomena, physicists were forced to embrace mathematics in a deeper way than they ever had before. It was the only guide that worked when intuition and our senses failed.
THE NATURE OF LIGHT had been debated as early as the 1600s, when Isaac Newton argued that it consisted of tiny corpuscles, while Robert Hooke insisted that it was made of waves. Newton’s enormous prestige pushed the wave theory into the background for a hundred years or so. But in the early 1800s, several experimental discoveries revived the debate. In 1801, Thomas Young discovered the interference of light waves. When a beam of light passes through two narrow, parallel slits, what we see on the other side is not two narrow bright bands, but a series of alternating dark and light bands with the brightest one right in the middle. This is easy to explain if you think of light as being like ripples of water in a tank, but not if you think about it as tiny particles of grapeshot.

Left Young’s Double Slit experiment.
Also, as early as 1665, Francesco Grimaldi had observed an effect he called diffraction—the apparent bending of light around a corner. Again, this was hard to square with Newton’s laws. (Remember that particles in motion with no force acting on them are supposed to go in a straight line.) Refraction, the bending of light as it passes through a prism, was also easier to explain with the wave theory than the particle theory. In 1818, Augustin Fresnel successfully accounted for all three of these phenomena—interference, diffraction, and refraction—with a theory in which light consists of transverse waves.‡
By the 1820s in France, and the 1830s in England (which was slower to shake off its hero-worship of Newton), the wave theory had gained the upper hand. But if light was a wave, what was the wave made of? It could not be a wave of air or any other fluid, because transverse waves don’t travel through fluids; they require a medium with elasticity, or the ability to “snap back” after being stretched. The great majority of physicists assumed that light traveled through some sort of “luminiferous aether,” but all efforts to detect this aether directly were in vain.
Meanwhile, the mysteries of electricity and magnetism were also deepening. In 1799, Count Alessandro Volta of Italy had invented the battery, which for the first time made it possible for physicists to experiment with steady electric currents. In 1820, Hans Christian Ørsted noticed, while preparing for a lecture, that when he turned on an electric current in a wire, it deflected a nearby compass needle. This was the first indication that electricity and magnetism were related. This clue was followed in 1831 by Michael Faraday’s discovery of electromagnetic induction. Faraday showed that a changing electric current in one coil would induce a temporary electric current in another one. Likewise, moving a magnet close to a coil would temporarily induce a current. This was, then, a reciprocal effect to the one Ørsted had noticed. Magnetism could induce electricity, but only if the strength of the magnetism was changing.

Above A coherent beam from a red Helium-Neon laser (632.8 nm) is used to illuminate two closely-spaced 25-micron-wide slits (double-slits).
THE MAN WHO WOVE all of these confusing clues into a beautiful theory was James Clerk Maxwell, a Scottish physicist. For those who think that great discoveries are always made in a flash of inspiration—like William Rowan Hamilton’s discovery of quaternions—Maxwell provides compelling evidence to the contrary. He worked on electromagnetism for several years, gradually painting the beautiful canvas we now know as Maxwell’s equations.
Maxwell’s first step, in 1855, was to take seriously Faraday’s description of the “lines of force” created by a magnet—lines that are easily seen if you sprinkle iron filings nearby. Faraday believed that the space around the magnet was surrounded by these “lines of force” even when no iron filings were present. Maxwell gave this invisible collection of curves a name—the magnetic field. He also postulated an electric field that conveys electric forces.
In the twenty-first century, we are completely accustomed to the idea that we live surrounded by electric and magnetic fields. So it may take a conscious effort to imagine how radical the idea was in the 1850s. What is an electric field? You can’t see it. You can’t touch it. How can you tell that it’s there?
Opposite Iron shavings are used to reveal magnetic field lines produced by two bar magnets.
An additional roadblock to Maxwell’s theory of fields was, again, the legacy of Newton. In Newton’s theory of gravity, planets attract each other from a distance, with a force proportional to the inverse square of their distance. For a while, electricity and magnetism seemed to work in exactly the same way. Physicists subscribed to the idea of “action-at-a-distance” as an article of faith. But Faraday and Maxwell questioned this conviction. They said the force between two charges, or two magnets, results from the field between them. In Newton’s universe, empty space is empty. But in Maxwell’s universe, it is humming with electric and magnetic potential.
Six years after his first paper, Maxwell added another stroke to his scientific painting. He envisioned electricity as an elastic force in the medium that electric and magnetic fields inhabit. It’s interesting to note that he had not yet abandoned the mechanical way of thinking and accepted the greater flexibility of mathematics. His second paper relies on an extremely complicated model, replete with spinning vortices to represent the magnetic fields and counterrotating “idle wheels” to represent the electric fields. All of this baroque machinery would be discarded in his third paper.
Elastic forces, as noted above, are exactly what is necessary to transmit transverse waves. Not only that, there is a simple formula for the speed of waves in any elastic medium. Reasoning by analogy, Maxwell was led to a formula for the speed of an electromagnetic wave. At the time, he was spending the summer at his estate in Scotland, and he could not look up the necessary physical constants to plug into the equation. But when he got back to his office at Kings College in London in the fall of 1861, he computed the speed as 310,740,000 meters per second. By comparison, in 1849, a French physicist named Armand Fizeau had measured the speed of light at 314,850,000 meters per second! (The currently accepted value is 299,792,458 meters per second. In fact, since 1983 the meter has been defined as the distance light travels in 1/299,792,458 of a second, so the speed of light is now prescribed by definition and is no longer an experimental constant.) It could not be an accident, thought Maxwell, that the two constants were so close. In his paper announcing the result, he wrote in italics: “We can scarcely avoid the inference that light consists in the transverse undulations of the same medium which is the cause of electrical and magnetic phenomena.”
BUT MAXWELL was not done. Having used a mechanical analogy to discover that electromagnetic waves and light waves are the same thing, he realized that he could forget about the vortices and the counterrotating gears, and derive the result solely from mathematics. What was left, by the time he wrote his third paper in 1865, was a simple set of four partial differential equations that relates the electric field (E) to the magnetic field (B) at any point in a vacuum.
By themselves, these equations are not a complete theory of electromagnetism. In particular, they lack any information on how material particles, such as electric charges and magnets, respond to the fields E and B. To use a Judeo-Christian analogy, Maxwell’s equations represent the state of the universe after God said “Let there be light,” and before he created anything else. To incorporate the material world, Maxwell added extra terms (representing charge density and current density) and extra equations.
Most of Maxwell’s equations were not actually original to him. The individual equations are known as Gauss’s law, Faraday’s law, and Ampère’s law. Maxwell’s only new contribution was a correction term that enters Ampère’s law when electric currents are taken into account. Nevertheless, the understanding that the equations could be brought together into a system, and the idea that magnetic and electric fields were the fundamental agent, were entirely due to Maxwell. So, too, was the discovery that the speed of light, c—the only experimental constant to be found in these equations—is a fundamental physical law.
Earlier it was mentioned that Euler’s equation eiπ + 1 = 0 was voted the most beautiful equation of all time by readers of Mathematical Intelligencer. In 2004, Physics World conducted a similar poll. It is no surprise that the readers of that publication chose Maxwell’s equations as the greatest ever. They are so simple, so symmetric, so hard-earned, and they explain so much.
Yet like the other revolutions described in this chapter, they made little impression at the time. Maxwell’s contemporaries just didn’t know what to make of them. “As long as I cannot make a mechanical model all the way through I cannot understand; and that is why I cannot get the electromagnetic theory,” said William Thomson, Lord Kelvin, in 1884 (the same Lord Kelvin who couldn’t “get” quaternions!).
But over time, the significance of Maxwell’s equations became more apparent. They predicted that electromagnetic waves could exist with different wavelengths—such as the waves we now call microwaves, infrared, ultraviolet, and X-rays. They predicted that such waves could be created by oscillating electric fields. In 1901, Guglielmo Marconi used precisely this principle to transmit the first radio waves. They implied that light itself can exert pressure. Sure enough, researchers in the twentieth century discovered the “solar wind,” which explained the centuries-old mystery of why comet tails point away from the Sun. And in 1905, as will be discussed further in the next chapter, they led Albert Einstein to the theory of relativity.
‡ A transverse wave is one that propagates at right angles to the motion of the individual particles in the wave. An example is “the wave” (sometimes called “the Mexican wave”) at a sports stadium. The individual particles (i.e., the fans) go up and down, but the wave moves around the stadium.