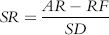
Appendix B
Formulas for Risk-Adjusted Return Measures
This appendix provides the formulas for the performance measures described in Chapter 8.
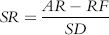
where:
SR = Sharpe ratio
AR = Average return (used as proxy for expected return)
RF = Risk-free interest rate (e.g., Treasury bill return)
SD = Standard deviation
The standard deviation is calculated as follows:
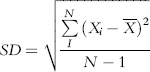
where:
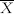= Mean
Xi = Individual returns
N = Number of returns
Assuming monthly data is used to calculate the Sharpe ratio, as is most common, the Sharpe ratio would be annualized by multiplying by the square root of 12. Note that the return is an arithmetic average return, not the compounded return.
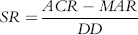
where:
SR = Sortino ratio
ACR = Annual compounded return
MAR = Minimum acceptable return (e.g., zero, risk-free, average)
DD = Downside deviation
where DD is defined as:
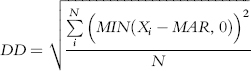
where:
Xi = Individual returns
MAR = Minimum acceptable return (e.g., zero, risk-free, average)
N = Number of data values
For example, if we define MAR = 0, then DD calculations will include only deviations for months with negative returns (the other months will equal zero).
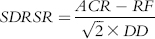
where:
SDRSR = Symmetric downside-risk Sharpe ratio
ACR = Annual compounded return
RF = Risk-free interest rate (e.g., T-bill return)
DD = Downside deviation
where DD is defined as:
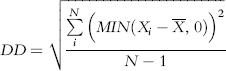
where:
Xi = Individual returns
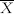= Benchmark return (e.g., mean, zero, risk free)
Since the SDR Sharpe ratio includes only the downside deviation, multiplying by the square root of 2 (a consequence of doubling the squared deviations) is equivalent to assuming the upside deviation is equal (i.e., symmetric) to the downside deviation. This proxy replacement of the upside deviation is what makes it possible to compare SDR Sharpe ratio values with Sharpe ratio values.
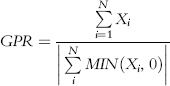
where:
Xi = Individual returns
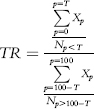
where:
Xp = Return at percentile p
T = Threshold percentile to calculate numerator of tail ratio (Implicit assumption: Lower percentile rankings represent higher return. For example, the top 10% of returns would be all returns less than T, where T = 10.)
Np<T = Number of returns below percentile
TNp>100−T = Number of returns above percentile 100-T
where:
ACR = Annual compounded return (expressed in decimal form)
NAV = Net asset value
j > i
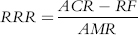
where:
ACR = Annual compounded return
RF = Risk-free return
AMR = Average maximum retracement = MRi/N
where:
N = Number of months
MRi = max(MRPNHi, MRSNLi)
where MRPNHi is the maximum retracement from prior NAV high, and is defined as:
where:
PNHi = Prior NAV high (prior to month i)
NAVi = NAV at end of month i
MRSNLi is the maximum retracement to a subsequent NAV low, and is defined as:
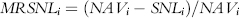
where SNLi is the subsequent NAV low (subsequent to month i)