More money has been lost through the mismeasurement of risk than by the failure to measure risk. It would be safer to drive a car without a speedometer than a speedometer that understated true speeds by 25 percent. If you had no mechanical gauge of speed, you would be conscious of that absence of information and take extra caution as a result. If, instead, you are relying on a speedometer you believe is providing correct readings but, in fact, is significantly understating actual speed, you will be more prone to an accident. Similarly, in trading and investment, relying on risk measurements that significantly understate true risk may be far more dangerous than not using any risk measurement at all. Indeed, many of the catastrophic losses suffered by investors have been a direct consequence of inaccurate risk measurement rather than the absence of risk measurement.
Perhaps the most spectacular example of how faulty risk measurement can lead to a drastically worse outcome than no risk measurement at all is the trillion-dollar-plus losses suffered by investors in 2007 and 2008 in debt securitizations linked to subprime mortgages, an episode detailed in Chapter 2. Investors bought these securities because the rating agencies assigned them AAA ratings—a risk evaluation that was based on assumptions that had no bearing to the underlying data (holdings that consisted entirely of unprecedentedly low-quality subprime mortgages). Imagine that investors were offered unrated debt securities whose collateral consisted of subprime mortgages with no down payment and no income, job, or asset verification, paying as little as a fraction of a percentage point above U.S. Treasury bonds. How much of these securities would they have bought? It is difficult to imagine any consequential amount being invested. Yet investors bought huge quantities of these securities because of the implicit assurance provided by credit ratings. The highly flawed risk assessment conducted by the credit rating agencies enabled enormous investor losses and widespread bank and financial institution failures that otherwise would not have occurred. Erroneous risk evaluations may give investors comfort where none is warranted, and in this sense are much worse than a complete absence of risk assessment, where the lack of such information would itself engender a far more cautious approach.
Volatility, as measured by the standard deviation, is the ubiquitous measure of risk. The standard deviation is a measure of dispersion. The more widespread returns are around the expected return (commonly assumed to be the average of historical returns), the higher the standard deviation. To provide a sense of what standard deviation values mean, assuming returns are normally distributed,1 returns would be expected to fall within one standard deviation of the expected return 68 percent of the time and within two standard deviations 95 percent of the time. For example, consider two managers, both with the same 15 percent average annual return (assumed to be the future expected return), but with widely different standard deviations of 5 percent and 20 percent. These two managers are compared in Table 4.1.
Table 4.1Comparison of Two Managers’ Performances

Although both managers have the same average return (and assumed future expected return), the uncertainty of the expected return is much greater for Manager B. There is a 95 percent probability that Manager A’s annual return will fall within the 5 percent to 25 percent range. Thus, for Manager A, there is a high probability that returns will exceed +5 percent, even in the worst case (at the 95 percent probability level). In contrast, the same 95 percent probability range allows for Manager B’s annual return to be anywhere between a very high 55 percent to a significant loss of −25 percent. It is in this sense of greater uncertainty of return that higher volatility is associated with greater risk. Typically, when investors refer to low-risk funds, they are talking about low-volatility funds (that is, funds with low annualized standard deviations).
In essence, the standard deviation measures the ambiguity of the expected return. It should be intuitively clear that if the standard deviation is low, it implies the return will be relatively close to the expected return, which is typically assumed to equal the average past return (assuming, of course, that the past return is considered the best estimate for the expected return). In contrast, if the standard deviation is high, it suggests that the actual return may vary substantially from the expected return. The standard deviation is a type of average deviation of returns from the mean—one in which bigger differences are weighted more heavily—and this description provides another intuitive interpretation of what the standard deviation represents.2
It is important to understand that the standard deviation measures the variability in returns and does not necessarily reflect the risk of losing money. Consider a fund, for example, that lost 1.0 percent every month. Such a fund would have a standard deviation of 0.0 (because there is no variability in returns), but an absolute certainty of losing money.3
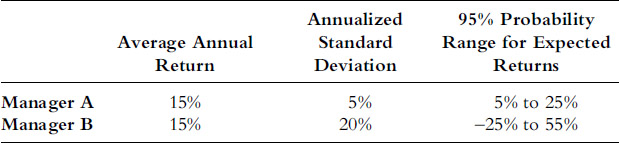
Let’s consider an example where the standard deviation is used to gauge a 95 percent probability range for future 12-month returns. Figure 4.1 shows the net asset value (NAV) of an actual fund, which we label “Fund X.” Although Fund X has relatively high volatility—10 percent monthly standard deviation, which annualizes to 35 percent—the high volatility appears to be more than counterbalanced by a lofty 79 percent average 12-month return. Fund X also appears to be a consistently strong performer with over 70 percent winning months, only two months with losses greater than 4 percent, and a maximum drawdown (equity peak to trough decline) limited to 15 percent, which lasted only one month. Fund X’s return and standard deviation numbers imply that there is a 95 percent probability that any 12-month return would fall in a 9 percent to 149 percent range [79% +/− (2 × 35%)]. This extremely wide range of possibilities is a consequence of the high volatility, but note that even the low end of the range implies that there is a 95 percent probability that any 12-month return will equal or exceed positive 9 percent.
Figure 4.1 Fund X: Steady Performer
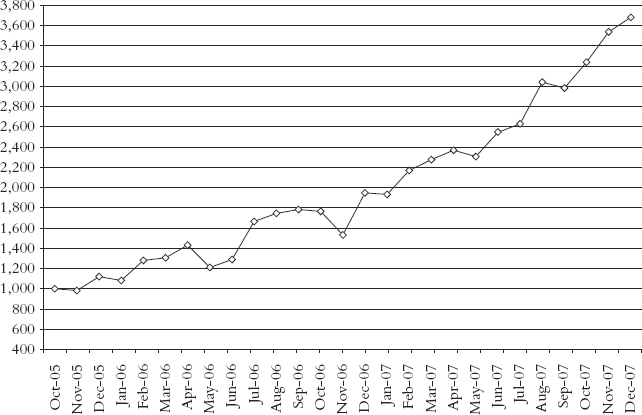
In Figure 4.2, we add one additional month of data. Based on this single additional month return, the most recent 12-month return drops from +89 percent to −66 percent! This negative 66 percent return is drastically below the positive 9 percent low end of the 95 percent probability range implied by the standard deviation. What happened? Why did the standard deviation provide such a highly misleading gauge of the low end of the probable return range?
Figure 4.2 Fund X: Oops!
The answers to these questions lead to an absolutely critical point regarding risk measurement: Volatility is useful in defining approximate downside risk only if historical returns are representative of the returns that can be expected in the future. While we can never be sure this assumption is true (at least not in the case of trading returns), there are definitely cases where we can be sure that it is false—and Fund X provides a prime example. To understand why this is the case, we have to examine the strategy employed by Fund X.
Note: Readers unfamiliar with options might find the primer on options in Appendix A helpful in better understanding the remainder of this section.
Fund X’s trading strategy involved selling out-of-the-money options. For example, if a stock index was trading at 1,000, this type of fund might sell calls with an 1,100 strike price (giving the buyer the right to buy the index at 1,100) and puts with a 900 strike price (giving the buyer the right to sell the index at 900). In the vast majority of cases, the market would not move sufficiently to reach either of these levels during the life span of the options, and the options would expire worthless. In this case, the fund would profit by the full premiums collected for the options sold. As long as the market did not witness any abrupt, very large price moves—that is, large enough to reach the strike prices of either the calls or the puts sold—the strategy would be profitable. Since markets only infrequently witness sudden, huge price moves, this type of strategy tends to register steady gains in a large majority of months.
The vulnerability in the strategy is that if the market witnesses a sharp price move in either direction, the strategy is prone to severe and accelerated losses. The losses occur for two reasons. First, there is a loss directly related to the price move. For example, if the market moves to 800, a seller of the 900 put would lose 100 points on the trade, less the small premium collected for selling the option (small because the option was far out-of-the-money when it was sold and would have been perceived as having a small probability of expiring in a profitable range). Second, volatility might increase sharply in the event of a steep market sell-off, further increasing the value of the options sold.
The real crux of the problem for the option seller, however, is that losses will increase exponentially as a price move continues. The reason for this behavior is related to the relationship between changes in the underlying market price and changes in the option price. The percentage that an option price will change for a given small change in the underlying market price is called the option’s delta. A delta of 50 (representative of options with strike prices near the market level) implies that the option will move by one-half point for every point move in the market. Out-of-the-money options, because they have a low probability of expiring with any value, will have low deltas. For example, the types of options sold by Fund X might have deltas as low as 0.1, meaning that initially, for every point the market moved toward its strike level, these options would have lost only 1/10 of a point. As a market move progressed, however, the delta would steadily increase, crossing the 0.5 level once the market reached the option strike price and approaching 1.0 as the option became more in-the-money. Thus, the exposure would steadily increase as the market moved adversely to the position, leading to accelerated losses. In short, the strategy pursued by Fund X is one that would win the majority of times, but occasionally could be vulnerable to a mammoth loss.
The period depicted in Figure 4.1 was generally one of low volatility and moderate price moves, a market environment very beneficial to an option selling strategy. Thus, it is hardly surprising that Fund X did very well. As for the large magnitude of its gains, these results simply imply that the fund was taking on a great deal of exposure (i.e., selling a lot of options). The types of episodes that could result in large losses for an option selling strategy did not occur during the period coincident with the fund’s prior track record. If an investor understood the strategy the fund was pursuing, it would have been clear that the historical record was not representative of the reasonable range of possibilities and hence could not be used to infer future risk, either through the standard deviation or by any other risk measure for that matter.
The core of the problem highlighted by the Fund X example is not so much a matter of volatility providing a misleading risk gauge, but rather the broader consideration that any track-record-based risk calculation would yield erroneous implications if the track record period is unrepresentative (e.g., it coincided with an overly favorable environment for the strategy). Volatility-based estimates underlie most erroneous risk evaluations simply because volatility is the track-record-based statistic most commonly used to measure risk.
The critical point is that risk assessments based on the past track record (the standard deviation or any other statistics) are prone to be highly misleading if the prior market environment for the strategy was more favorable than what could generally be anticipated over a broader time frame. The reason why investment risk estimates so often prove to be fatally flawed is that they are based only on visible risk—that is, losses and volatility evident in the track record—and do not account for hidden risks—that is, sporadic event-based risks that failed to be manifested during the track record period.
Hidden risk is risk that is not evident in the track record because the associated risk event did not occur during that time period. Hidden risks occur only sporadically, but when they occur, they can have a major negative impact. The key types of hidden risk include:
Figure 4.3 HFR Equity Hedge Fund Index versus S&P 500 (January 1, 2003 = 100)
Figure 4.4 HFR Fixed Income Corporate Index Monthly Returns (Six-Month Average) versus Credit Spread (Moody’s Baa Yield Minus 10-Year Treasury Note Yield)
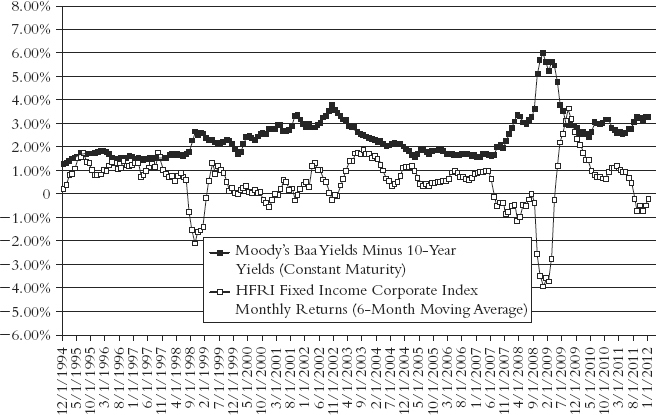
In all these instances (except perhaps for market risk, where adverse periods may be more frequent), strategies prone to the foregoing event risks will exhibit relatively smooth performance and limited equity drawdowns during most periods, interspersed with occasional episodes of large drawdowns. In effect, these strategies exhibit two different phase states with sharply contrasting characteristics. Drawing general conclusions based on a period that contains only the benign phase can prove harmful to investor health.
An adequate risk assessment requires not only an examination of the track-record-based risk statistics (e.g., standard deviation, maximum drawdown), but also an evaluation of hidden risks. If hidden risks are pertinent to the strategy, then track-record-based risk statistics alone will be seriously deficient as risk indicators. While track-record-based risk statistics are readily quantifiable, it is not at all clear how one could assess and weigh risks that did not occur in a meaningful way in the track record. So the key question is: Although the inclusion of hidden risk may be critical to risk evaluation, from a practical standpoint, how can this risk be identified and measured?
Identifying and assessing hidden risk (susceptibility to event risk not evident in the track record) requires a combination of quantitative and qualitative approaches.
Even when the track record does not contain loss episodes remotely reflective of the risk inherent in a fund or strategy, it still can be used to identify these risks. Some examples of track-record-based measures that can be used to identify hidden risks include:
The track record is only a starting point in risk assessment. While evidence of high risk in the track record indicates the potential for high risk in the future, the reverse is not true: Low risk in the track record does not necessarily imply low risk. Investors need to ask themselves the question: What was the source of past returns? Specifically, investors need to determine to what extent past returns were due to taking on market exposure or credit risk, selling volatility, holding illiquid positions, or using leverage—all approaches that can lead to smooth or high returns in most times, but also abrupt losses in risk-averse environments.
The qualitative assessment can be quantified by assigning a rating score to each risk considered. For example, each risk factor can be assigned a value between 1 and 10, with 1 representing very low risk and 10 extremely high risk. Using such an approach, a foreign exchange (FX) fund trading only G-7 currencies might be assigned a liquidity risk of 1, while a fund with $1 billion under management trading microcap stocks might have a liquidity risk of 8 to 10. As another example, a market neutral equity fund would have a market risk rating of 1 or 2, while a long-only fund would have a risk rating closer to 10. In this way, each risk can be assessed and codified. Although the approach is unavoidably subjective, it can be very helpful in highlighting potentially risky funds, regardless of whether any significant risk is evident in the track record. Consider two funds, both of which have equivalent low volatility and moderate equity drawdowns, but differ in their qualitative risk ratings as shown in Table 4.2. Whereas the track records might suggest they have equivalent risk, the qualitative risk assessment score approach clearly indicates that Fund B is far riskier.
Table 4.2Exposure to Selected Risk Factors

Volatility is often viewed as being synonymous with risk—a confusion that lies at the heart of the mismeasurement of risk. Volatility is only part of the risk picture—the part that can be easily quantified, which is no doubt why it is commonly used as a proxy for risk. A comprehensive risk assessment, however, must also consider and weigh hidden (or event) risks, especially since these risks may often be far more important.
The confusion between volatility and risk often leads investors to equate low-risk funds with low-volatility funds. The irony is that many low-volatility funds may actually be far riskier than high-volatility funds. The same strategies that are most exposed to event risk (e.g., short volatility, long credit) also tend to be profitable a large majority of the time. As long as an adverse event does not occur, these strategies can roll along with steadily rising NAVs and limited downside moves. They will exhibit low volatility (relative to return) and look like they are low-risk. But the fact that an adverse event has not occurred during the track record does not imply that the risk is not there. An option selling strategy, such as Fund X, will appear to be low-risk (relative to return) as long as volatility remains muted. But as soon as volatility spikes, the risk explodes. The behavior of investments vulnerable to event risk operates in two radically different states: the predominant phase when conditions are favorable and the sporadic phase when an adverse event occurs. It is folly to estimate overall performance characteristics based on just one of these phases. Assuming that low volatility implies that a fund is low-risk is like assuming a Maine lake will never freeze based on daily temperature readings taken only during the summer.
Funds can be both low-volatility and high-risk. Funds that fall into both categories would have the following characteristics:
Our intention is to caution that low volatility does not necessarily imply low risk. There is, however, no intention to suggest that low volatility implies high risk. Of course, some low-volatility funds will also be low-risk funds. The key is determining the reason for the low volatility. If low volatility can be attributed to a strategy that assumes a trade-off of frequent moderate wins in exchange for the risk of occasional large losses (e.g., selling out-of-the-money options, leveraged long credit positions), then the risk evaluation must incorporate the implications of an adverse event, even if one did not occur during the fund’s track record. If, however, low volatility can be attributed to a strategy that employs rigorous risk control—for example, a risk management discipline that limits losses to a maximum of ½ percent per trade—then low volatility may indeed reflect low risk.
Not only does volatility, as typically measured by the standard deviation, often dramatically understate risk in circumstances when hidden risks apply, but in some cases, volatility can also significantly overstate risk. Some managers pursue a strategy that curtails the downside but allows for large gains. Consider the example of Fund Y, in which the manager buys out-of-the-money options at times when a large price move is anticipated. The losses on these trades would be limited to the premiums paid, but the gains would be open-ended. If, on balance, the manager was successful in timing these trades, the track record might reflect high volatility because of large gains. The risk, though, would be limited to the losses of the option premiums. In effect, the manager’s track record would exhibit both high volatility and low risk.
Fund Y is not the inverse of Fund X, which consistently sold out-of the-money options. The opposite strategy of consistently buying out-of-the-money options might have limited monthly losses, but it would certainly be prone to large cumulative drawdowns over time because of the potential of many consecutive losing months. Also, since option sellers are effectively selling insurance (against price moves), it is reasonable to assume that they will earn some premium for taking on this risk. Over broad periods of time, consistent sellers of options are likely to earn some net profit (albeit at the expense of taking on large risk exposure), which implies an expected net negative return for buyers of options. In order for a long option strategy to be successful, as well as to exhibit constrained drawdowns over time, the manager needs to have some skill in selecting the times when options should be brought (as opposed to being a consistent buyer of options).
So high volatility is neither a necessary nor a sufficient indicator of high risk. It is not a necessary indicator because frequently the track record volatility may be low, but the strategy is vulnerable to substantial event risks that did not occur during the life span of the record (that is, hidden risks). It is not a sufficient indicator because in some cases, high volatility may be due to large gains while losses are well controlled.
Value at risk (VaR) is a worst-case loss estimate that is most prone to serious error in worst-case situations. The VaR can be defined as the loss threshold that will not be exceeded within a specified time interval at some high confidence level (typically, 95 percent or 99 percent). The VaR can be stated in either dollar or percentage terms. For example, a 3.2 percent daily VaR at the 99 percent confidence level would imply that the daily loss is expected to exceed 3.2 percent on only 1 out of 100 days. To convert a VaR from daily to monthly, we multiply it by 4.69, the square root of 22 (the approximate number of trading days in a month). Therefore the 3.2 percent daily VaR would also imply that the monthly loss is expected to exceed 15.0 percent (3.2% × 4.69) only once out of every 100 months. The convenient thing about VaR is that it provides a worst-case loss estimate for a portfolio of mixed investments and adapts to the specific holdings as the portfolio composition changes.
There are several ways of calculating VaR, but they all depend on the volatility and correlations of the portfolio holdings during a past look-back period—and therein lies the rub. The VaR provides a worst-case loss estimate assuming future volatility and correlation levels look like the past. This assumption, however, is often wildly inappropriate. For example, in early 2007, the VaR of a portfolio of highly rated subprime mortgage bonds would have suggested minuscule risk because the prior prices of these securities had been extremely stable. There would not have been even a hint of the catastrophic risk inherent in these securities, since VaR can only reflect risk visible in prior price movements.
If the past look-back period is characterized by a benign market environment and a risk-seeking preference by investors, the VaR is likely to greatly underestimate the potential future loss if market conditions turn negative and investor sentiment shifts to risk aversion. During such liquidation phases, not only will the volatility levels of individual holdings increase sharply, but correlation between different markets will also rise steeply, a phenomenon known as “correlations going to 1.” When different markets are moving in tandem, the risk at any volatility level will be magnified. In 2008, losses by funds of hedge funds greatly exceeded the extremes suggested by VaR because virtually all hedge fund strategies witnessed large losses at the same time, even those that normally had low correlations with each other. The diversification that fund of funds managers counted on disappeared. The cause was the domino effect of liquidation, as large losses in some hedge funds caused investors in need of liquidity to liquidate other unrelated fund holdings, setting off a self-reinforcing liquidation cycle. With the vast majority of hedge funds trying to liquidate the same side of trades as other hedge funds, the transitory imbalance between supply and demand resulted in extremely adverse liquidation prices and widespread losses across virtually all hedge fund styles.
VaR provides a good risk estimate for normal market conditions, which prevail most of the time. The problem is that the greatest risk lies in the sporadic episodes where markets are seized by panic liquidations and act abnormally. VaR is like an automobile speedometer that is perfectly accurate at speeds below 60, but provides inaccurately low readings for speeds above 60. It is dangerously wrong exactly at those times when accuracy is most critical! By providing a statistically based worst-case risk measure, VaR may induce unwarranted complacency in investors regarding the risk in their portfolios. In this sense, an overreliance on VaR as a risk gauge may be more dangerous than not using any risk measurement at all.
Consider an example of two hedge funds both of which utilize long/short strategies in high yield bonds and hedge to neutralize interest rate risk. Which fund portfolio seems riskier?
Although it sounds as if portfolio B has much higher risk, the reverse might be true:
Moral: Credit quality alone can be a very poor indicator of risk. Risk is not a function of quality, but rather quality relative to price.
Standard risk measures are often poor indicators of actual risk. Major sources of risk frequently fail to be reflected at all by typical risk metrics. The most widely used risk measure—volatility—will fail to indicate a host of risks that are intermittent in nature. Even worse, the types of strategies that are particularly prone to sporadic large losses may often exhibit extended periods of low volatility. Thus investors seeking low-risk investments and using volatility as their guideline may perversely be drawn to higher-risk investments.
Any risk assessment that is solely based on the track record is inherently flawed. Investors also need to consider the various hidden risks discussed in this chapter—risks that are often not evident in the track record. A comprehensive risk analysis may begin with track-record-based measurements but must also include an understanding of the investment strategy and its inherent risks, as well as an evaluation of the risk management policies of the manager. Judging risk based solely on the track record is akin to an insurance company issuing a policy on a five-year-old home based strictly on its assessed value and prior claim history without considering its location—even if it is located in a floodplain! Just because there have not been any floods since the house was built doesn’t mean the risk is low. Absence of evidence of high risk is not evidence of low risk.
1Normally distributed means that returns will fall within the typical bell-shaped pattern—more returns near the mean (i.e., average) and fewer and fewer returns for values more distant from the mean. A normal distribution is commonly assumed in a wide range of calculations in finance because it usually provides a reasonable approximation and because it greatly simplifies the calculation of many statistics. (Any normally distributed data series can be fully represented by just two numbers: the mean and the standard deviation.) In reality, however, many markets and return streams deviate from normal distributions by having more instances of returns widely removed from the mean—a characteristic that causes the assumption of a normal distribution to lead to a serious underestimation of the probabilities associated with extreme events. A classic example of this failing was the October 19, 1987, stock market crash, discussed in Chapter 2, an event that the assumption of a normal distribution would have implied was impossible. Here we are concerned with illustrating the concept of standard deviation, which implicitly assumes returns are normally distributed to make probability statements about future returns, rather than evaluating the validity of the normal distribution assumption.
2The standard deviation calculation is readily available in any spreadsheet program, but for those readers who want to know how it is calculated, there are five simple steps:
The squaring of the differences between individual returns and the mean (step 2) assures that negative deviations have same impact on the standard deviation as positive deviations (rather than offsetting them) and also acts to give greater weight to wider deviations. Step 4 counterbalances the squaring of deviations in step 2. The formula for the standard deviation is:
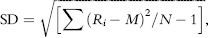
where Ri is the individual return for month “i”, M is the mean, and N is the number of returns.
3This quirky example was provided by Milt Baehr, the cofounder of Pertrac, in a conversation we had years ago.
4Assuming interest rate levels do not increase by enough to offset yield reduction due to credit narrowing.
5Mathematically, beta is equal to correlation times the ratio of the series standard deviation to the benchmark standard deviation. So, for example, if the correlation equals 0.8 and the series has a standard deviation half as large as the benchmark, the beta would be equal to 0.4.