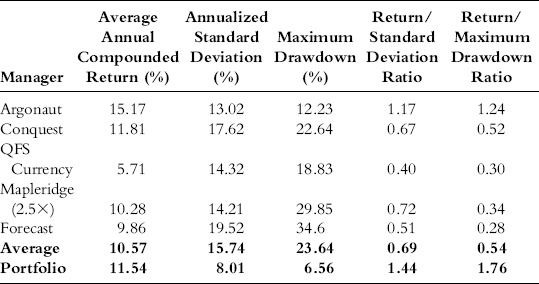
Fred, a research analyst at a fund of funds firm, is given the task of constructing a portfolio of futures, global macro, and foreign exchange (FX) managers. After some research, he reports back to his boss, Sam, with a suggested five-manager portfolio shown in Table 18.1. The five managers have an average annualized return of 10.57 percent and an average annualized standard deviation of 15.74 percent. The average maximum drawdown of the five managers is 23.64 percent. Because of the benefits of diversification, the portfolio statistics are far better: an annualized return of 11.54 percent with a standard deviation of only 8.01 percent and a much reduced maximum drawdown of 6.56 percent.
Table 18.1 Five-Manager Portfolio Statistics, January 2001 to June 2010

Sam reviews the suggested portfolio and then calls Fred into his office. “The managers you picked appear to be an interesting mix,” he says, “but I am troubled that there are only five managers in the portfolio. We need to have much more diversification. I would like to add these 10 managers I have been looking at.” He hands Fred the list of managers in Table 18.2.
Table 18.2 Ten Added Manager Statistics, January 2001 to June 2010

Sam continues, “Interestingly, the average return of my 10 managers is almost identical to the average return of your five managers (10.50 percent versus 10.57 percent), and the risk statistics are virtually equivalent—the average standard deviation is slightly higher (16.68 percent versus 15.74 percent), but the average maximum drawdown is slightly lower (22.03 percent versus 23.64 percent). So this group of managers appears almost exactly equivalent to your managers in terms of performance, but adding them will triple the number of managers in the portfolio and give us the diversification we need. Run the statistics on this combined 15-manager portfolio and get back to me.”
Fred does the analysis. He is surprised to discover that tripling the number of managers in the portfolio significantly increases the portfolio risk, even though, on average, the added managers had equivalent risk statistics to the original managers. The results are shown in Table 18.3. The portfolio average annual return does not change much—it falls slightly from 11.5 percent to 11.3 percent—but the risk statistics deteriorate significantly: The portfolio standard deviation increases by more than a third from 8.0 percent to 10.9 percent, and the maximum drawdown nearly doubles from 6.6 percent to 12.0 percent.
Table 18.3 Fifteen-Manager versus Five-Manager Portfolio Statistics
| Five-Manager Portfolio | 15-Manager Portfolio | |
| Average annual compounded return (%) | 11.54 | 11.31 |
| Annualized standard deviation (%) | 8.01 | 10.86 |
| Maximum drawdown (%) | 6.56 | 12.04 |
| Return/standard deviation ratio | 1.44 | 1.04 |
| Return/maximum drawdown ratio | 1.76 | 0.94 |
What is going on? Why does adding more managers with equivalent performance cause the portfolio volatility to increase—the exact opposite effect sought by the additional diversification? The answer is that diversification depends not only on the number of managers, but also on the degree of correlation among the managers (versus each other and the total portfolio). Fred’s original five-manager portfolio consisted of managers that were almost completely uncorrelated with each other: an average pair correlation of 0.07. In contrast, Sam’s list of 10 managers all employed a similar methodology—systematic trend following—and therefore were highly correlated with each other (an average pair correlation of 0.69). As a result, rather than reducing risk through diversification, adding these managers was roughly equivalent to adding one grossly oversized position to the portfolio. If Sam had instead suggested adding a single manager to the original five, but at 10 times the allocation size of the other managers, we would intuitively expect the risk to increase. The situation is not much different when instead of adding one manager with 10 times the allocation size of other managers, we instead add 10 highly correlated managers.
The diversification of Fred’s original five-manager portfolio would still be unsatisfactory due to its exposure to the randomness and idiosyncratic risks detailed in the previous chapter, but it would nonetheless be better diversified than the 15-manager portfolio. The critical point is that for diversification to work, the investments added to the portfolio must have a low average correlation to the existing investments and to each other.
The lesson to investors is that you can’t judge the diversification of a multimanager portfolio by the number of managers. Some types of portfolios may be particularly prone to unsatisfactory diversification, even if the number of managers appears more than sufficient. One example is commodity trading advisor (CTA) portfolios, similar to the one we described in our illustration. Since the majority of CTAs utilize systematic trend-following techniques and most such approaches are highly correlated with each other, CTA portfolios can often be poorly diversified, even if they contain a large number of managers. As another example, long/short equity hedge portfolios are vulnerable to insufficient diversification because the majority of managers in this trading strategy style are significantly correlated to the equity market. In fact, for some strategies (e.g., convertible arbitrage), it would be virtually impossible to create a well-diversified portfolio, because manager performance is often more dependent on the investment environment for the strategy than on the manager’s own individual methodology.
How can an investor judge whether a portfolio is insufficiently diversified? A simple gauge and an easily obtainable statistic is the average pair correlation—that is, the average of all manager pair correlations in the portfolio. For example, in a 20-manager portfolio, there would be 190 possible manager pairs and therefore 190 pair correlations. The average of these correlations provides an indicator of the degree of diversification in a portfolio. Any portfolio manager should be able to easily provide the investor with the average pair correlation for the portfolio. Although there are no clear-cut definitions of what constitutes adequate or inadequate diversification, I would suggest the following broad guidelines for the portfolio average pair correlation: A value greater than 0.50 reflects inadequate diversification; a value between 0.30 and 0.50 suggests that diversification is somewhat inadequate; a value less than 0.20 indicates that the managers are very well diversified. There are, however, circumstances when unsatisfactory diversification may be entirely acceptable. Specifically, if a portfolio is being considered as a component of a broader mix of investments, the fact that it is not adequately diversified as a stand-alone investment may not be a problem if it is well diversified with the other holdings in the investor’s total portfolio.
Increasing the number of investments in a portfolio can sometimes lead to less diversification rather than more. Diversification is a function of both the number of holdings and, even more importantly, the degree to which they are uncorrelated. A portfolio with a small number of uncorrelated holdings is effectively more diversified than a portfolio with a large number of significantly correlated assets.