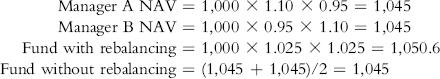
Many years ago, I worked for a brokerage firm where in addition to being the research director, I was also the department expert on the quantitative evaluation of commodity trading advisors (CTAs). This job responsibility got me thinking about better methods for constructing multimanager funds. At one point, it became apparent to me that if all the managers had equivalent expected future performance, the return/risk ratio would be increased if the total equity were rebalanced monthly, bringing the managers back to an equal percentage allocation.1
The assumption that all managers would have equivalent future performance did not mean that such an outcome was expected literally, but rather that one could not predict anything about the relative ranking order of the future performance of the selected managers. (Although the past ranking order was certainly known, my implicit assumption was that the past ranking was a very poor indicator of the future ranking.)
The following analogy occurred to me: The assumption of equivalent performance could be thought of as monthly performance results being represented by a series of cards—each card representing one month—with each manager’s set of results corresponding to a different shuffle of the same cards. Since all managers are assumed to have the same set of monthly results (that is, the same set of cards in a different order), and since reduced variability implies increased return (see Chapter 5), it seemed that the return/risk ratio based on the average of cards in each month—the mathematical equivalent of a monthly rebalancing—would have to be equal to or higher than the return of any individual set of cards (that is, the performance of each manager). In other words, if one had no a priori reason to believe that any manager in the selected group would perform better in the future than the other managers, a monthly rebalancing of equity would yield an equal or higher end return than a static one-time allocation.
As a very simple example to provide a feel of the preceding conclusion, assume a two-manager fund with a two-month performance period, in which Manager A makes 10 percent in the first month and loses 5 percent in the second, while Manager B witnesses the reverse order of monthly results. The respective net asset values (NAVs) would then be:
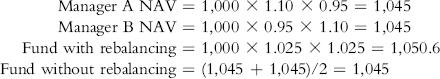
In each month, one manager gains 10% on half the assets (or 5% on total assets), while the other manager loses 5% on the other half of assets (or 2.5% on total assets). Therefore in each month, there is a net gain of 5% − 2.5% = 2.5%.
Note in this simple example that the monthly rebalancing fund realizes a higher return than the fund that does not rebalance assets.
To check whether the idea of monthly rebalancing held up in the real world, I conducted the following empirical experiment. I selected 30 groups of six managers each from the available database. For each group I calculated the NAV over a three-year period for the following two situations:
I found that the leveraged/rebalanced fund almost invariably outperformed the fund without rebalancing. Even more striking, however, was the observation that the return of the leveraged/rebalanced fund was usually about in line with the best or second-best manager in the group, while the maximum drawdown and standard deviation (measures of risk) were about in line with the lowest or second-lowest figures among the group of managers. In other words, by employing a monthly rebalancing strategy with leverage, it was possible to approximate the return of the best return managers in the group and the risk of the best (lowest) risk managers in the group. In effect, rebalancing with leverage was a means of optimizing the future performance—achieving return/risk characteristics in line with those managers in a selected group who would perform best in the future.
I was very excited about my discovery. I next tried to convince management at my company of the logic and attractiveness of a multimanager fund that would be structured around the concept of monthly rebalancing and leverage. A number of meetings ensued, but I felt my idea was going nowhere. Then I struck upon the idea of applying my rebalancing/leverage strategy to a hypothetical fund consisting of the firm’s five single-manager funds, most of which had disappointing track records and therefore, not surprisingly, were regarded with less than enthusiasm by management. As it turned out, the theoretical multimanager fund I constructed using my strategy had a performance profile that was only slightly inferior to the best manager in the group and far superior to the four other managers. Since the best manager could only have been selected with hindsight, the potential advantage of my approach seemed both obvious and compelling.
“This should clinch it,” I thought. I made some color charts illustrating these performance comparisons and set up another meeting with the division manager whose approval was vital. After I completed my 15-minute presentation, I leaned back, waiting for the division head to extol the wisdom of my proposal.
Instead he exclaimed, “You mean you want to take from the winners and give to the losers!” in a tone that suggested I had just proposed the virtues of matricide.
“No,” I replied, “you’re missing the point. The assumption is that we believe all the managers in the fund are winners—that’s presumably why we picked them in the first place. What we are doing is taking from winners during their winning periods and giving it to other winners during their losing periods.” But all the logic in the world could not prevail. The division head simply could not get beyond the “shocking” nature of my proposal. My idea never went anywhere.
In reconsidering this episode for this book, I realized my original analysis was flawed. The database I used to draw my samples contained only active managers (that is, surviving managers). I could not pick managers who had gone out of business—a group more likely to exhibit poor performance. If I had drawn samples that included defunct managers, perhaps monthly rebalancing, which effectively was equivalent to taking from the winners and giving to the losers, would not have been beneficial. Possibly, it might even have been detrimental. In short, my original analysis was subject to survivorship bias. There was no way of telling whether the apparent large benefit I found in rebalancing in my original analysis was sufficient to overcome this bias.
To test the rebalancing concept in a new analysis that avoided survivorship bias, I obtained the complete CTA database from Stark & Company (www.starkresearch.com)—a data set that included both existing and defunct managers. I randomly selected 10 portfolios of 10 managers each from this complete list,2 assuming equal allocations and a January 1, 2005, start date. I then compared the total period (2005 to 2010) portfolio results obtained assuming no further allocation adjustments with the results obtained by rebalancing the portfolios to equal allocations each month.
The rules for handling managers who went out of business were simple:
Table 19.1 compares the portfolio rank versus the underlying CTAs in each portfolio in terms of return (average annual compounded), standard deviation (a risk proxy),3 and the return/risk ratio. Since there are 11 items being ranked in each case (the portfolio and its 10 component investments), the median rank is six. The best performance ranking is “1” and the worst “11.” For the standard deviation, lower values are defined as better ranking (that is, lower rank number). Both sets of portfolios (with and without rebalancing) rank significantly better than the median levels in terms of return, standard deviation, and the return/risk ratio, a clear demonstration of the benefits of diversification. The average rank for return is the same for both portfolios with and without rebalancing, but the portfolios with rebalancing generate better ranks for both risk and return/risk.
Table 19.1 Ranks of Portfolios versus CTAs in Portfolios
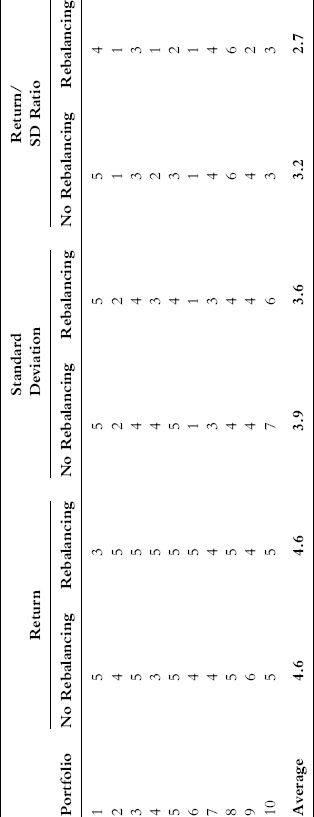
Table 19.2 compares the no-rebalancing and rebalancing portfolios in terms of return/risk—the key measure. (A portfolio with higher return/risk but lower return than another portfolio can be made to generate a higher return with equal or lower risk by using leverage.) The rebalanced portfolio generated a higher return/risk ratio in eight of the 10 portfolios, and the two exceptions were only marginally lower. On average, the rebalanced portfolios had an 18 percent higher return/risk ratio.
Table 19.2 Portfolio Return/Risk Comparison

Table 19.3 shows the percentage of the portfolios for which rebalancing resulted in better performance for each of three metrics: return, standard deviation (proxy for risk), and return/standard deviation ratio. Rebalancing resulted in lower risk and higher return/risk in 80 percent of the portfolios, but provided a higher return only half the time. Since rebalancing reduces volatility in most of the portfolios, Table 19.3 also looks at the same comparison for a portfolio with rebalancing and a modest 10 percent leverage. This slight modification resulted in 80 percent of the portfolios with rebalancing outperforming the portfolios without rebalancing in terms of both return and return/risk, with 70 percent of the portfolios still having lower risk.
Table 19.3 Percentage of Portfolios for Which Rebalancing Outperforms No Rebalancing
| Rebalancing | Rebalancing with 10% Leverage | |
| Return | 50% | 80% |
| Standard deviation | 80% | 70% |
| Return/SD ratio | 80% | 80% |
As Tables 19.2 and 19.3 illustrate, in our trial, which fully eliminated survivorship bias, rebalancing still seemed to provide significant performance improvement. These results offer empirical evidence that supports the hypothesis that rebalancing—routinely “taking from the winners and giving to the losers”—will tend to improve performance, but it by no means proves this contention. A more conclusive test would have required repeating the experiment for far more than 10 randomly selected portfolios—a requirement that exceeded both my patience in repeating Excel spreadsheet calculation steps and my programming ability, which is nil. Readers, however, can duplicate the same comparison between rebalancing and no rebalancing on the past returns of their own portfolios. Although some readers who conduct this experiment will find that rebalancing actually would have been detrimental, I believe most will discover that it would have been beneficial. The comparison should be made in terms of return/risk, not return, since rebalancing will tend to lower risk, a benefit that, if desired, can be translated into higher return through leverage.
If the managers in a portfolio had identical performance (defined as identical monthly returns in different orders), it would be a mathematical certainty that rebalancing would improve performance. This point was demonstrated in nonrigorous fashion at the start of this chapter using the card shuffling analogy. Therefore, if there is no strong reason to expect one or more of the selected managers in a portfolio to outperform the other managers in the future, rebalancing would provide a mathematical edge.
At different times, market conditions will be favorable for different strategies. A strategy that works particularly well during one period may perform very poorly in another period. For example, if markets are generally experiencing choppy trading-range conditions, countertrend strategies are likely to do very well, while trend-following approaches get whipsawed. If market conditions then change so that there are many prevalent trends, trend-following methods will be very profitable, while countertrend traders will suffer losses. Rebalancing keeps the asset allocation among the different market strategies represented by different managers constant. Without rebalancing, assets would be more heavily concentrated in the strategies that worked best in the past. If market conditions then change, the largest asset allocations would be in the strategies that are most vulnerable. In effect, rebalancing helps mitigate the negative impact of the inevitable shifts in market conditions, which can result in being overweight, an outperforming strategy when that strategy has run its course and is about to turn negative; and being underweight, a strategy that is about to have a huge run.
Another way of understanding why rebalancing works is that it effectively forces profit taking when a manager witnesses an upside excursion and increases investment when a manager experiences a drawdown. Therefore, when a manager witnesses the inevitable retracement following an especially profitable run, the investment with that manager will be smaller than it would have been without rebalancing. Conversely, when a manager experiences a rebound after a drawdown, the investment with that manager will be greater than it would have been without rebalancing.
For simplicity of exposition, in this chapter we have assumed that rebalancing means a return to equal allocations each month. Rebalancing, however, neither requires nor implies equal allocation. Frequently, there will be good reason to use unequal allocations among managers. For example, it would be entirely reasonable, if not preferable, to give smaller allocations to higher-risk managers. If allocations are unequal, rebalancing would simply mean returning to the target allocations each month. For example, if a portfolio manager decides that because of higher risk, Manager A should get half the allocation of other managers, rebalancing would adjust the allocations to maintain this ratio in subsequent months.
Theoretical arguments and empirical evidence suggest that monthly rebalancing of equity provides a means of enhancing the expected return/risk characteristics of multimanager portfolios. This does not mean that the use of rebalancing would improve the performance (that is, increase the return/risk ratio) of every multimanager fund; it does, however, mean that rebalancing would probably improve the performance of a majority of such funds. In other words, for any given multimanager fund, the odds favor that the use of rebalancing would enhance performance. Portfolio managers and investors can test rebalancing on their own portfolios by comparing their actual results with the results that would have been obtained if allocations were rebalanced to their initial allocation percentages each month.4
Given the apparent advantage of rebalancing, why is this method typically unused? The answer to this question is simple: human nature. The idea of shifting assets from traders who have just performed best in a given portfolio to those who performed worst goes against natural human instincts. Following these instincts, however, will usually lead to incorrect market decisions. One of the requirements for success in the markets is the ability to make decisions based on evidence, not based on what feels comfortable.
1 If the managers have disparate risk levels, it would make more sense to define equal allocation in risk-adjusted terms (rather than equal dollar terms)—a concept discussed in Chapter 21. Doing so would not alter the conclusions of this chapter.
2 I used the Excel function Randbetween to generate 100 random numbers (10 portfolios times 10 managers) with a top threshold set equal to the total number of all active and defunct managers in the database.
3 For CTAs who trade highly liquid futures, hidden risk (as detailed in Chapter 4) is not usually a problem, and the standard deviation (a volatility measure) is a reasonable proxy for risk.
4 Such a test would be complicated by the addition or redemption of holdings, as is likely to occur over time. One simplifying assumption for handling such situations is to rebalance monthly to the same percentage allocations that prevailed in the last month in which there was a portfolio change. In effect, the percentage allocation targets used for rebalancing would change each time there was a portfolio addition or redemption.