In SfM, we would like to recover both the poses of cameras and the position of 3D feature points. We have just seen how simple 2D pair matches of points can help us estimate the essential matrix and thus encode the rigid geometric relationship between views: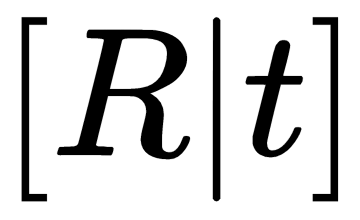 
. The essential matrix can be decomposed into 
and 
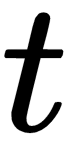by way of SVD, and having fou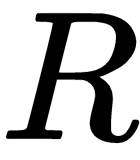nd 
and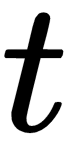 
, we proceed with finding the 3D points and fulfilling the SfM task for the two images.
We have seen the geometric relationship between two 2D views and the 3D world; however, we are yet to see how to recover 3D shape from the 2D views. One insight we had is that given two views of the same point, we can cross the two rays from the optic center of the cameras and the 2D points on the image plane, and they will converge on the 3D point. This is the basic idea of triangulation. One simple way to go about solving for the 3D point is to write the projection equation and equate, since the 3D point (
) is common,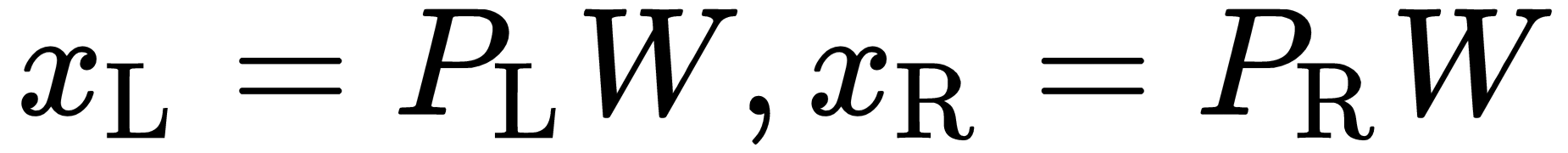 
, where the 
matrices are the 
projection matrices. The equations can be worked into a homogeneous system of linear equations and can be solved, for example, by SVD. This is known as the direct linear method for triangulation; however, it is severely sub-optimal since it makes no direct minimization of a meaningful error functor. Several other methods have been suggested, including looking at the closest point between the rays, which generally do not directly intersect, known as the mid-point method.
After getting a baseline 3D reconstruction from two views, we can proceed with adding more views. This is usually done in a different method, employing a match between existing 3D and incoming 2D points. The class of algorithms is called Point-n-Perspective (PnP), which we will not discuss here. Another method is to perform pairwise stereo reconstruction, as we've seen already, and calculate the scaling factor, since each image pair reconstructed may result in a different scale, as discussed earlier.
Another interesting method for recovering depth information is to further utilize the epipolar lines. We know that a point in image L will lie on a line in image R, and we can also calculate the line precisely using 
. The task is, therefore, to find the right point on the epipolar line in image R that best matches the point in image L. This line matching method may be called stereo depth reconstruction, and since we can recover the depth information for almost every pixel in the image, it is most times a dense reconstruction. In practice, the epipolar lines are first rectified to be completely horizontal, mimicking a pure horizontal translation between the images. This reduces the problem of matching only on the x axis:
The major appeal of horizontal translation is disparity, which describes the distance an interest point travels horizontally between the two images. In the preceding diagram, we can notice that due to right overlapping triangles: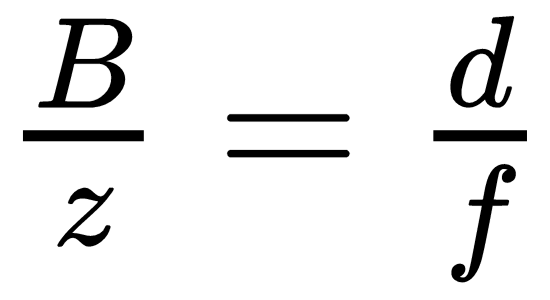 
, which leads to 
. The baseline 
(horizontal motion), and the focal length 
are constant with respect to the particular 3D point and its distance from the camera. Therefore, the insight is that the disparity is inversely proportional to depth. The smaller the disparity, the farther the point is from the camera. When we look at the horizon from a moving train's window, the faraway mountains move very slowly, while the close by trees move very fast. This effect is also known as parallax. Using disparity for 3D reconstruction is at the base of all stereo algorithms.
Another topic of wide research is MVS, which utilizes the epipolar constraint to find matching points from multiple views at once. Scanning the epilines in multiple images all at once can impose further constraints on the matching features. Only when a match that satisfies all the constraints is found is it considered. When we recover multiple camera positions, we could employ MVS to get a dense reconstruction, which is what we will do later in this chapter.