While affine transforms are useful for stitching scanned documents (for example, from a flatbed scanner), they cannot be used for stitching photo panoramas. For stitching photos, we can employ the same process to find a homography, a transform between one plane and another, instead of an affine transform, which has eight degrees of freedom, and is represented in a 3 x 3 matrix as follows:
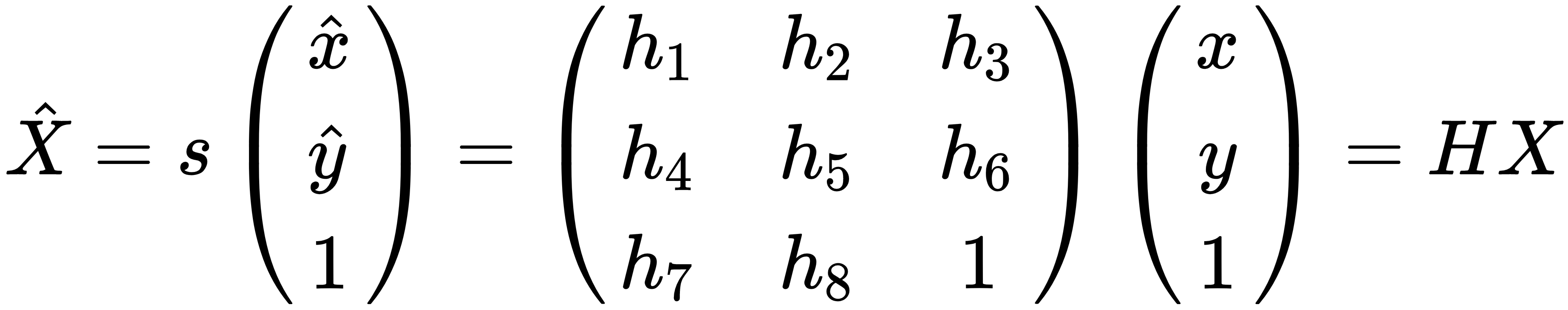
Once a proper matching has been found, we can find an ordering of the images to sequence them for the panorama, essentially to understand how the images relate to one another. In most cases, in panoramas the assumption is that the photographer (camera) is standing still and only rotating on its axis, sweeping from left to right, for example. Therefore, the goal is to recover the rotation component between the camera poses. Homographies can be decomposed to recover rotation, if we regard the input as purely rotational: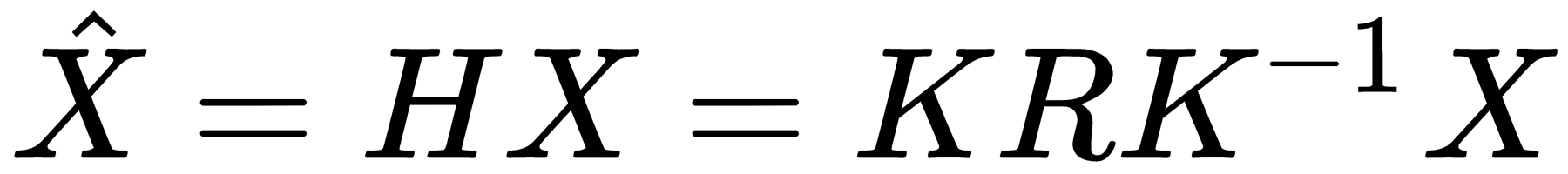 
. If we assume the homography was originally composed from the camera intrinsic (calibration), matrix K, and a 3 x 3 rotation matrix R, we can recover R if we know K. The intrinsic matrix can be calculated by camera calibration ahead of time, or can be estimated during the panorama creation process.