Our images begin with a projection. The 3D world they see through the lens is flattened down on the 2D sensor inside the camera, essentially losing all depth information. How can we then go back from 2D images to 3D structures? The answer, in many cases with standard intensity cameras, is MVG. Intuitively, if we can see (in 2D) an object from at least two views, we can estimate its distance from the cameras. We do that constantly as humans, with our two eyes. Our human depth perception comes from multiple (two) views, but not just that. In fact, human visual perception, as it pertains to sensing depth and 3D structure, is very complex and has to do with the muscles and sensors of the eyes, not just the images on our retinas and their processing in the brain. The human visual sense and its magical traits are well beyond the scope of this chapter; however, in more than one way, SfM (and all of computer vision!) is inspired by the human sense of vision.
Back to our cameras. In standard SfM, we utilize the pinhole camera model, which is a simplification of the entire optical, mechanical, electrical, and software process that goes on in real cameras. The pinhole model describes how real-world objects turn into pixels and involve some parameters that we call intrinsic parameters, since they describe the intrinsic features of the camera:
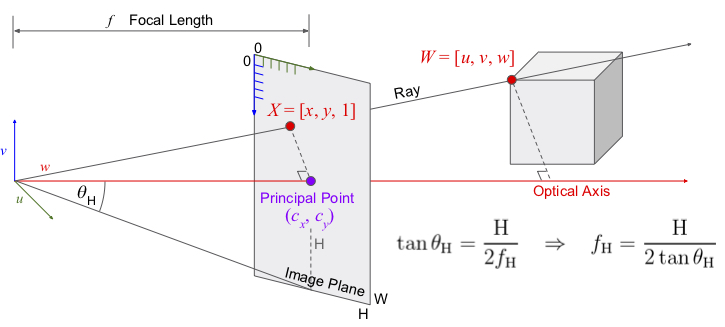
Using the pinhole model, we find the 2D positions of a 3D point on the image plane by applying a projection. Note how the 3D point 
and the camera origin form a right-angled triangle, where the adjacent side equals 
. The image point 
shares the same angle with adjacent 
, which is the distance from the origin to the image plane. This distance is called the focal length, but that name can be deceiving since the image plane is not actually the focal plane; we converge the two for simplicity. The elementary geometry of overlapping right-angled triangles will tell us that 
; however, since we deal with images, we must account for the Principle Point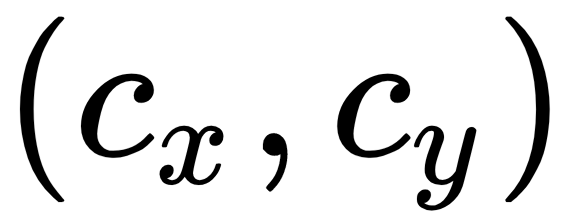 
and arrive at 
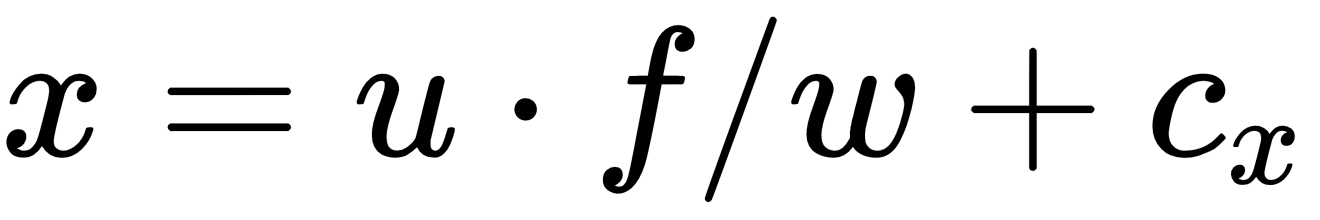. If we do the same for the 
axis, this follows:
The 3 x 3 matrix is called the intrinsic parameters matrix, usually denoted as 
; however, a number of things seem off about this equation and require explanation. First, we're missing the division by 
, where did it go? Second, what is that mysterious 
that came about on the LHS of the equation? The answer is homogeneous coordinates, meaning we add a 
at the end of the vector. This useful notation allows us to linearize these operations and perform the division later. At the end of the matrix multiplication step, which we might do for thousands of points at once, we divide the result by the last entry in the vector, which happens to be exactly the 
we're looking for. As for 
, this is an unknown arbitrary scale factor we must keep in mind, which comes from a perspective in our projection. Imagine we had a toy car very close to the camera, and next to it a real-sized car 10 meters away from the camera; in the image, they would appear to be the same size. In other words, we could move the 3D point 
anywhere along the ray going out from the camera and still get the same 
coordinate in the image. That is the curse of perspective projection: we lose the depth information, which we mentioned at the beginning of this chapter.
One more thing we must consider is the pose of our camera in the world. Not all cameras are placed at the origin point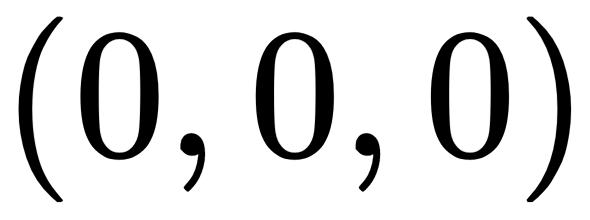 
, especially if we have a system with many cameras. We conveniently place one camera at the origin, but the rest will have a rotation and translation (rigid transform) component with respect to themselves. We, therefore, add another matrix to the projection equation:
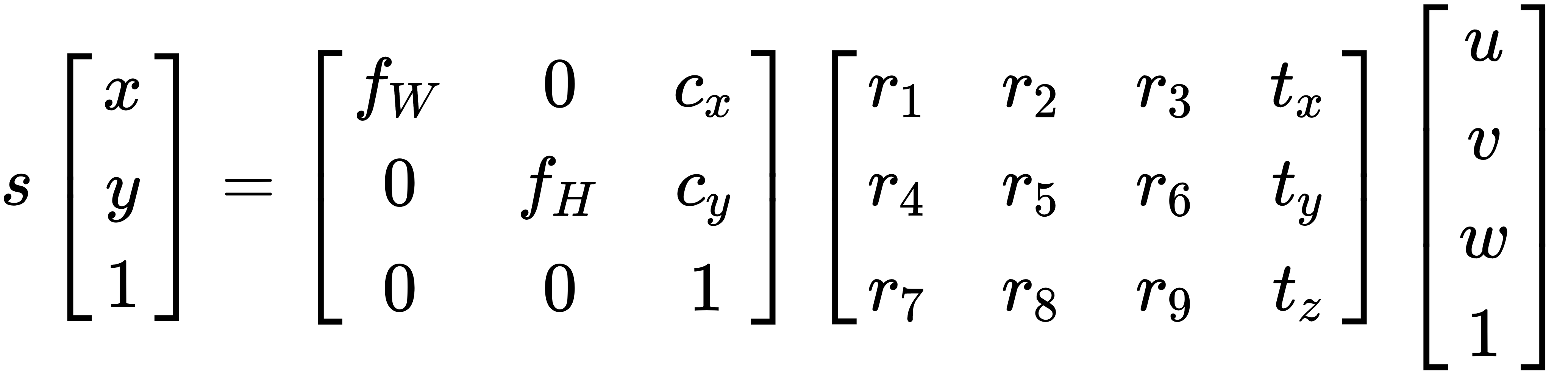
The new 3 x 4 matrix is usually called the extrinsic parameters matrix and carries 3 x 3 rotation and 3 x 1 translation components. Notice we use the same homogeneous coordinates trick to help incorporate the translation into the calculation by adding 1 at the end of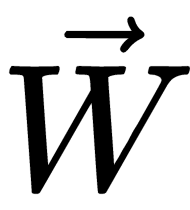 
. We will often see this entire equation written as 
in the literature:
Consider two cameras looking at the same object point. As we just discussed, we can slide the real location of the 3D point along the axis from the camera and still observe the same 2D point, thus losing the depth information. Intuitively, two viewing angles should be enough to find the real 3D positions, as the rays from both viewpoints converge at it. Indeed, as we slide the point on the ray, in the other camera looking from a different angle, this position changes. In fact, any point in camera L (left) will correspond to a line in camera R (right), called the epipolar line (sometimes known as epiline), which lies on the epipolar plane constructed by the two cameras' optical centers and the 3D point. This can be used as a geometric constraint between the two views that can help us find a relationship.
We already know that between the two cameras, there's a rigid transform 
. If we want to represent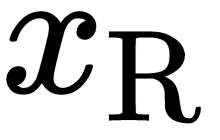 
, a point in camera R, in the coordinate frame of camera L, we can write 
. If we take the cross product 
, we will receive a vector perpendicular to the epipolar plane. Therefore, it follows that 
since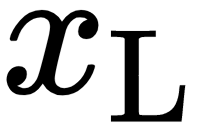 
lies on the epipolar plane and a dot product would yield 0. We take the skew symmetric form for the cross product and we can write 
, then combine this into a single matrix 
. We call 
the essential matrix. The essential matrix gives us an epipolar constraint over all pairs of points between camera L and camera R that converge at a real 3D point. If a pair of points (from L and R) fails to satisfy this constraint, it is most likely not a valid pairing. We can also estimate the essential matrix using a number of point pairings since they simply construct a homogeneous system of linear equations. The solution can be easily obtained with an eigenvalue or singular value decomposition (SVD).
So far in our geometry, we assumed our cameras were normalized, essentially meaning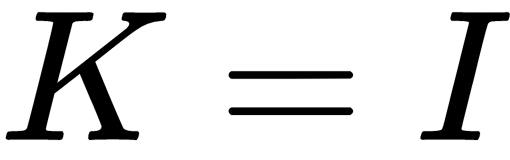 
, the identity matrix. However, in real-life images with particular pixel sizes and focal lengths, we must account for the real intrinsic. To that end, we can apply the inverse of 
on both sides: 
. This new matrix we end up with is called the fundamental matrix, which can be estimated right from enough pairings of pixel coordinate points. We can then get the essential matrix if we know 
; however, the fundamental matrix may serve as a good epipolar constraint all on its own.