When a transformation has been achieved locally between all photo pairs, we can further optimize our solution in a global step. This is called the process of bundle adjustment, and is widely constructed as a global optimization of all the reconstruction parameters (camera or image transforms). Global bundle adjustment is best performed if all the matched points between images are put in the same coordinate frame, for example, a 3D space, and there are constraints that span more than two images. For example, if a feature point appears in more than two images in the panorama, it can be useful for global optimization, since it involves registering three or more views.
The goal in most bundle adjustment methods is to minimize the reconstruction error. This means, looking to bring the approximate parameters of the views, for example, camera or image transforms, to values such that the re-projected 2D points back on the original views will align with minimal error. This can be expressed mathematically like so:
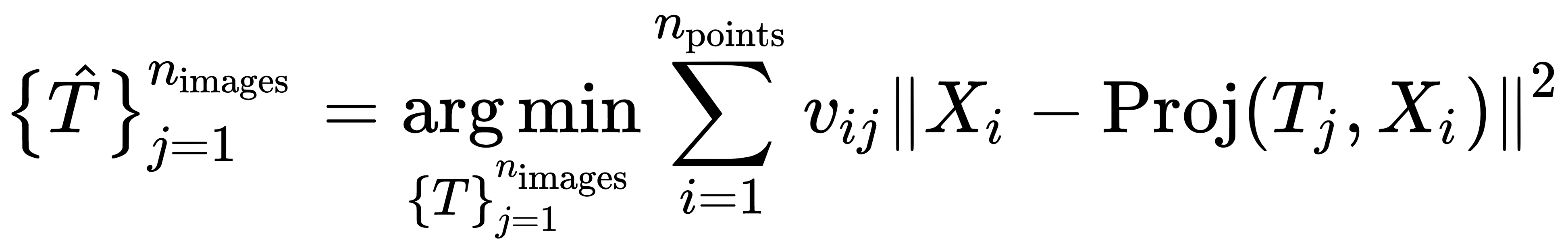
Where we look for the best camera or image transforms T, such that the distance between original point Xi and reprojected point Proj(Tj, Xi) is minimal. The binary variable vij marks whether point i can be seen in image j, and can contribute to the error. These kinds of optimization problems can be solved with iterative non-linear least squares solvers, such as Levenberg-Marquardt, since the previous Proj function is usually non-linear.