
I will be sufficiently rewarded if when telling it to others you will not claim the discovery as your own, but say it was mine.
Thales, sixth century BC
TWO QUESTIONS about the prediction of eclipses in the ancient world continue even today to cause controversy in academic circles. The first is whether England’s famous megalithic stone circle at Stonehenge was ever used to predict eclipses. The second concerns the truth of the report by ancient Greek historians that the philosopher Thales predicted an eclipse of the Sun in the early part of the sixth century BC.
The opinion of the great majority of respectable historians, archaeologists and anthropologists today is that both these claims are false. In the first instance, critics argue that the very idea of such an advanced proto-science as eclipse prediction being practised by megalithic people is absurd, considering that they could not even write. Also, it is argued, the alignments of stones at Stonehenge which the theory’s proponents believe were used in eclipse prediction are not accurate enough to track the exact position of the Moon in advance of an eclipse. In the second instance, the case against Thales rests on the fact that no historian of science today can figure out how he could have made the prediction. Therefore, it is argued, he didn’t do it!
It is important to ascertain how eclipses could have been predicted at all by the ancients. The accomplishment would have to have been based on the discovery of a repeating cycle of eclipses. Alternatively, a repeating cycle of the Moon’s motion might have been found and correlated with previous eclipses. Two such cycles have been discussed in this book: the 18.61-year cycle of the rotation of the Moon’s line of nodes, and the saros cycle of eclipses, with a period of 18 years and 10 days. It is important not to confuse these two cycles, which have nearly the same period. They are completely unrelated. The claims for Stonehenge as a predictor of eclipses are based on the first of these cycles, the rotation of the nodes. The feasibility of Thales’ prediction, as proposed recently by a Russian historian of science, is based on the second cycle, the saros.
The variation of the rising and setting points of the Sun and the Moon on the horizon surprises many people. The Sun doesn’t simply rise in the east and set in the west. In northern latitudes like those of the British Isles, the Sun rises quite far north of east in summer, and sets well north of west. In winter, the Sun rises south of east and sets south of west. This is a result of the tilt of the Earth’s rotational axis: in summer, the northern hemisphere leans into the Sun; in winter, it leans away from the Sun. The farther north an observer moves, the greater the difference between the rising and setting points of the Sun and Moon along the horizon.
Given this wide seasonal swing, it would seem natural for ancient observers at high northern or southern latitudes to have used ‘horizon astronomy’. Calendars and almanacs can be devised by checking the motion of the Sun and Moon along the horizon rather than the shadow length of a post in the ground or the height of the midday Sun. Instead of watching the Sun at noon or the Moon at midnight, the Stonehenge people watched the rising and setting points on the horizon.
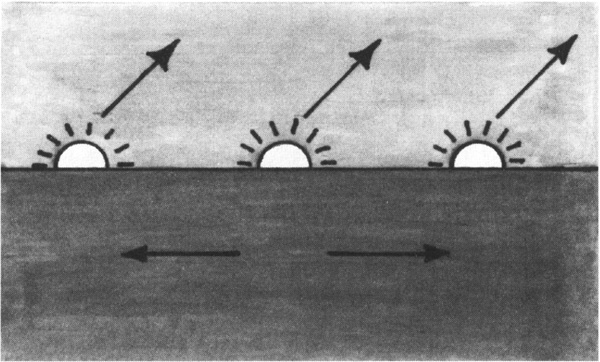
Figure 4.1. Horizon astronomy.
They would soon have noticed that the position at which the Sun rises on the eastern horizon oscillates back and forth between a northern and a southern extreme. These two extremes, known as the ‘standing still’ positions, are the points on the horizon where sunrise stops its motion along the horizon, turns, and starts to cycle back to the other extreme. These ‘standing still’ points for the Sun are marked at Stonehenge by principal alignments of the standing stones.
The Sun’s motion is clearly all-important for dividing up the year and preparing a calendar. But not so the Moon. Yet it seems that those who built Stonehenge were also intensely interested in the Moon’s motion. Was it to further sub-divide the year, or to predict eclipses? The full Moon’s extreme positions on the horizon were also marked at Stonehenge. The variations of moonrise are even wider than those of sunrise. The alignments through the standing stones at Stonehenge to the extreme positions of the Sun and Moon are shown in Figure 4.2. The extreme swings along the horizon of the rising and setting of the full Moon take exactly 18.61 years. This includes the swings between the major ‘standstills’, a to a, and the minor ‘standstills’, b to b, within the 18.61 year cycle.
The realisation that the principal alignments in Stonehenge were with the extreme positions of the Sun and the Moon came about in 1965, when the British-born astronomer Gerald Hawkins, a professor of astronomy at Boston University, published Stonehenge Decoded. In this book Hawkins describes a computer analysis of the principal alignments of the viewing directions between the stones. He found that all the principal alignments pointed towards the extreme positions on the horizon of the rising and setting of either the Sun or the full Moon. In other words, Stonehenge was a megalithic astronomical observatory incorporating a calendar based on the Sun and the Moon. The book caused a sensation among the ancien régime of archaeologists – experts on the megalithic period who could not accept the attribution of an advanced technology to such an early society.
Figure 4.2. The principal alignments at Stonehenge (after Hawkins 1965).
Hawkins, Gerald S., Stonehenge Decoded (Doubleday, New York, 1965)
However, in what seemed to be a speculative elaboration of his computer work, Hawkins proposed that in addition to the principal alignments of the extremal positions of the Sun and Moon, Stonehenge was also used to predict eclipses. This was a radical idea which the British cosmologist Fred Hoyle further developed several years later. Hoyle proposed that Stonehenge was used to follow the positions of the lunar nodes around the ecliptic. When full or new Moon occurs near a node, the ‘danger zone’, an eclipse can occur.
Obviously, if the cycle of the nodes was known, the Moon could be tracked very carefully to determine any relationship between the cycle and eclipses that were observed at Stonehenge. It seems that the builders were convinced that by accurately locating the extreme positions of the Moon, they could predict when an eclipse would take place. There are problems with this. The Moon moves about twelve times faster than the Sun through its extreme positions, and consequently the positions are more difficult to mark. Critics have argued that a much more accurate sighting system would be required than is available at Stonehenge.
Because of the rotation of the line of nodes, the Moon swings back and forth between its extreme positions in the same period as the nodal cycle. One result of this is the unusual movement of the winter full Moon near the central axis of Stonehenge, aligned with the marker known as the Heelstone, as shown in Figure 4.3. If the rising of the winter full Moon is studied for many years, and marked by sight lines, it will be found that its rising point swings back and forth across the Heelstone with a cycle of 18.61 years. When the full Moon rises in the centre of this swing, over the Heelstone, the point where the sun rises on the summer solstice, it is eclipsed.
Figure 4.3. The cycle of the extreme horizon positions of the rising and the setting of the Moon at Stonehenge. The period of the cycle is 18.61 years. The letters a and b indicate the ranges of the major and minor standstills, respectively.
It seems that the Stonehenge people were at least close to being able to predict eclipses. However, they have left no written records that might persuade scholars that the alignments at the site should be examined more closely. Unless the remains of an astronomer-priest are found in a megalithic tomb on Salisbury Plain with artefacts from this enigmatic structure, it is unlikely that the controversy over Stonehenge as an eclipse predictor will ever be settled.
The claim that the Greek philosopher Thales (624–546 BC) predicted a solar eclipse in the sixth century BC is a different matter, for in this case there are many sources of information and speculation. Although no written works of Thales have survived, Greek historians such as Herodotus and Thucydides wrote extensively about his achievements.
Figure 4.4. Thales (from a sculpture at Hadrian’s Villa, Tivoli).
Thales, who came from the classical city of Miletus on the Ionian coast, was the first known Greek philosopher, scientist and mathematician. A figure of enormous prestige, Thales was the only philosopher who ranked among the Seven Wise Men of Ancient Greece. This was particularly significant because his status as a Wise Man came from his reputation as a philosopher, not from a position in politics, as was the case for the others accorded this honour. Some consider him to have been the teacher of Pythagoras, though it may be only that he advised Pythagoras to travel to Egypt and Chaldea. From Eudemus of Rhodes (about 320 BC) we know that Thales studied in Egypt and brought Egyptian learning to Greece. All ancient sources ascribe to him the introduction of mathematical and astronomical sciences into Greece. Since none of his writing survives, it is difficult to determine his philosophy and to be certain about his mathematical discoveries. Nevertheless, he is credited with five theorems of elementary geometry.
In spite of all his other achievements, Thales’ fame has always rested on the reports of ancient Greek historians that he successfully predicted a solar eclipse. The most frequently quoted source is Herodotus. One of the most important writers of ancient Greece, Herodotus is often called ‘the father of history’. In his famous chronicles of ancient Greek times, The Histories, he recounted the story of the war between the Lydians and the Medes. It was a long war which had been waged for five years with neither side gaining prominence. Herodotus tells how, during a battle on 28 May 585 BC,
Figure 4.5. A solar eclipse in the sixth century BC stops a battle between the Lydians and the Medes.
the day was turned to night. Thales of Miletus had foretold this loss of daylight to the Ionians, fixing it within the year in which the change did indeed happen. So when the Lydians and the Medes saw the day turned to night they ceased from fighting and both were more zealous to make peace.
It is wonderful to think that a war could be ended by a spectacular natural phenomenon which humbles belligerent armies, as the drawing shown in Figure 4.5 tries to capture. But more interesting to us today is Thales’ prediction. How did he do it?
Some sceptical scholars have pointed out that the writings of ancient historians, Herodotus included, contain examples of portentous eclipses which never took place – now referred to as ‘literary eclipses’. One report in Herodotus describes how Xerxes and his Persian armies observed an eclipse just before they set out from Sardis to conquer the Greeks. But no such eclipse can be found by modern computations to match the date of the invasion. Clearly, there was a political motive for creating a celestial omen: it would indicate that the gods were with Xerxes and a great change was about to take place. But Thales could have had no political motive for making an eclipse prediction. In fact, Thales’ prediction may have been the real event that inspired other, fictional accounts.
It is not only Herodotus who tells us about Thales’ eclipse prediction. Diogenes Laertius, in his Lives of Eminent Philosophers, refers to Xenophanes as having been amazed by Thales’ achievement. This is significant since Xenophanes lived in the same century as Thales, and could therefore be a more reliable source. Nevertheless, respected modern scholars, Thomas-Henri Martin in the nineteenth century and Otto Neugebauer more recently, have concluded that the story of the prediction is nothing but a myth. It could be argued that such scepticism is unfair when viewed in the light of the usual procedures used in classical studies. Evidence from independent sources for Thales’ prediction seems too strong to be denied. Yet, if we are to accept the reality of Thales’ achievement, there remain the questions of how and why he made his prediction.
In 1994 Dmitri Panchenko of the Academy of Sciences in St Petersburg published a paper in the Journal of the History of Astronomy in which he attempted to solve this controversy among modern scholars. In his opening paragraph, he sets the scene:
The prediction of a solar eclipse by Thales is one of the most celebrated events in the history of Greek science. It astonished his contemporaries and it has astonished modern scholars. Unfortunately, we have no ancient account of the method that facilitated Thales’ extraordinary achievement, and all modern attempts at the reconstruction of such a method seem to have failed. It has been argued that any reliable prediction of a solar eclipse was impossible before the time of Hipparchus, more than four centuries later.
Panchenko reviews all the reasons for dismissing the claim, including the fact that the method used by Thales for his prediction has never been substantiated. He accepts that there was a tradition at the time to credit famous men with discoveries they did not make. Furthermore, he is not daunted by the fact that most of today’s historians of science treat the story as apocryphal. In spite of all this, he sets out to show the feasibility of Thales’ prediction.
The first approach would be to assume that Thales knew of the saros cycle of 223 synodic months or 6,585.32 days. There has been wide agreement among scholars that this was the method he used for the prediction. But there is a problem here. In the sixth century BC no such saros cycle was known for solar eclipses at a given location on Earth because consecutive eclipses in a saros cycle are separated by about 115 degrees of longitude, one-third of the way around the world. Communications in the sixth century BC being what they were, there is no way that Thales could have known of solar eclipses which took place that far from Ionia. Furthermore, the saros was not discovered by the Chaldean astronomers until about 400 BC. So by this argument Thales could not have used consecutive 18.61-year saros eclipses as a basis for prediction.
Some scholars have suggested that Thales merely explained to the Ionians how an eclipse occurs, and declared that such a natural event was not at all dangerous and that it would probably reappear some time in the future. But this raises another problem. As eclipses were already known to the Greeks of this era, it seems unlikely that Thales’ fame would result merely from his announcing that an eclipse might happen some time in the future. No, he would have had to do better than that. He would have needed to predict the date, or at least the year, of a particular solar eclipse.
Modern calculations of the dates of solar eclipses visible from Ionia during this period have allowed Panchenko to develop a plausible theory of why and how Thales predicted the solar eclipse. Panchenko agrees that Thales probably wanted to assure his compatriots that all was well in the heavens. He wished to emphasise that the series of three solar eclipses observable from Ionia within a few years of one another, listed in Table 4A, was a natural coincidence. To ease their anxiety further, Thales predicted when the next one would occur. It was quite unusual and indeed unsettling for three consecutive eclipses, the third of which was total, to be visible from the same location on Earth within the space of three years. The third eclipse in the sequence, that of 28 May 585 BC, must have been frightening for the Ionians. Considerably larger in magnitude than the two previous eclipses, its central path of totality crossed northern Anatolia.
Table 4A. Three solar eclipses visible from Ionia.
Date of Solar Eclipse |
Magnitude (at Miletus) |
29 July 588 BC |
0.836 |
14 December 587 BC |
0.835 |
28 May 585 BC |
0.905* |
*Total eclipse in northern Anatolia.
Though not particularly superstitious, the Ionian Greeks would have seen the Sun’s light blotted out on three occasions in the space of three years, and must have been quite edgy. Both Plutarch and Thucydides reported anxiety among the Greeks at the times of eclipses. Plutarch tells a revealing story in his Life of Pericles:
Pericles was commander of the Grecian naval forces and when the whole fleet was in readiness, and Pericles on board his own galley, there happened an eclipse of the Sun. The sudden darkness was looked upon as an unfavourable omen, and threw the sailors into the greatest consternation. Pericles, observing that the pilot was much astonished and perplexed, took his cloak, and having covered the pilot’s eyes with it, asked him if he found anything terrible in that, or considered it a bad omen? Upon his answering in the negative, he asked ‘Where is the difference, then, between this and the other, except something bigger than my cloak causes the difference?’
According to Herodotus, Thales made a public announcement of his prediction, so it must have been at a gathering like the Pan-Ionian festivals, which were held every four years. Panchenko suggests that Thales was not so bold as to predict the exact date, but finds evidence in classical sources to support the estimate of the year: he said something like ‘You will see a solar eclipse before our next festival.’
So, did this happen? There were two solar eclipses soon after which were visible from this region, on 21 September 582 BC and 16 March 581 BC. As the Greek year began at the summer solstice in June, both these eclipses would have been in the same ‘calendar’ year for the Ionians, 582/581 BC – the same year in which Thales received public recognition of his intellectual prominence by becoming the first Greek to be accorded the status of ‘Wise Man’. This answers the ‘why’, and also the ‘when’. But do we know ‘how’ the sage of Ionians predicted that the eclipses of 582/581 BC would occur before the next Pan-Ionian festival?
These were turbulent times in Greece and the ancient Near East. Just before the period in which Thales lived and worked in Ionia, the Assyrian kingdom was under continuous attack from the Chaldeans and the Medes, finally being destroyed during the period 626–600 BC. Major cities in Assyria, such as Nineveh, ceased to exist. It is likely that many of the empire’s displaced intelligentsia – particularly trained astronomers and astrologers – would have emigrated to the court of the new power centre, Egypt. With the Assyrians, Egypt had a common enemy in the Babylonians. Politically, then, this was a time quite conducive to the spread of astronomical knowledge from Assyria to Egypt and then to Ionia.
It is not so far-fetched to imagine that Thales, a leading scribe from Ionia’s most important city, may have met astronomers from Assyria in Egypt at the court of the Pharaoh Neccho (610–595 BC). There are many indications in other writings of Thales’ travels to Egypt. In fact, Miletus had an important fortified maritime colony on the Nile delta. Thales, the originator of astronomy among the Greeks, could have learned of the eclipse records kept by the Chaldean priests and astrologers of Assyria in the seventh and eighth centuries BC. Now, the third and final eclipse in a triple saros of 54 years and one month can be seen from the same location as the last eclipse of the previous triple saros. Three shifts of the saros cycle brings the eclipse back to the original longitude, as indicated in Figure 3.2. The eclipses listed in Table 4B were recorded by Assyrian astronomers in Nineveh. This series of three triple saros cycles would enable Thales to predict the eclipse of 16 March 581 BC.
Table 4B. Three consecutive predecessors in the triple saros for an eclipse on 16 March 581 BC (from observational records at Nineveh).
Date of Eclipse |
Magnitude |
9 December 744 BC |
0.80 |
54 years later: |
|
11 January 689 BC |
0.83 |
54 years later: |
|
12 February 635 BC |
0.88 |
54 years later: |
|
16 March 581 BC |
prediction |
It is possible that another cycle of 27 years was noticed first. For example, the following list of eclipses from Assyrian records are all separated by 27 years:
9 December 744 BC*
10 December 717 BC
11 January 689 BC*
12 January 662 BC
12 February 635 BC*
Those asterisked are, of course, separated by 2 x 27 = 54 years, the triple saros cycle. Also, the large gap after the eclipse of 2 February 635 BC would certainly have hinted at the triple saros cycle of 3 x 18 = 2 x 27 = 54 years.
Table 4C gives selected major solar eclipses observable at Nineveh in the period 689–635 BC, together with eclipses probably known to Thales, having been observed at Miletus. If all this information was made available to Thales through his Egyptian connections, his acceptance of a 54-year eclipse cycle is clearly probable. By comparing the two sets of eclipse data, Thales would have been able to establish a 54-year cycle, without knowing that it consisted of a triple 18-year cycle. The eclipse in 596 BC would have provided Thales with a crucial test for the continuity of the 54-year series. This eclipse was difficult to observe from Egypt or Babylon, but Thales could not have missed it from Miletus. It began at about 15:00, in the afternoon, and reached its maximum at 16:12, 38 minutes before sunset. The magnitude of 0.69 would have been quite enough to attract the attention of the inhabitants of Miletus.
Table 4C. Solar eclipses observed at Nineveh and Miletus, 689–635 BC.
Nineveh |
Miletus |
Time difference |
12 Jan 662 BC |
13 Feb 608 BC |
54 |
15 Apr 657 BC |
18 May 603 BC |
54 |
7 Jun 651 BC |
9 Jul 597 BC |
54 |
21 Feb 650 BC |
23 Dec 596 BC |
54 |
6 Apr 648 BC |
9 May 594 BC |
54 |
11 Nov 641 BC |
14 Dec 587 BC |
54 |
12 Feb 635 BC |
16 Mar 581 BC† |
54 |
†Predicted by Thales
Dmitri Panchenko thus creates his case for Thales’ prediction, based on the 54-year cycle, not of the eclipse of 28 May 585 BC, but of the eclipse of 16 March 581 BC, visible from Miletus. The hypothesis depends only on the quite reasonable assumption that Thales was acquainted with Eastern astronomy, and brings into agreement classical texts and the history of science. The date fits perfectly with Herodotus’ testimony and with an independent report in Greek archives of the year of Thales’ public recognition as one of the ‘Seven Wise Men’ of ancient Greece. There is still some confusion over the timing of the battle between the Medes and the Lydians which was halted by the eclipse, because another eclipse occurred at around the same time, 21 September 582 BC. Nevertheless, Panchenko seems to have answered the sceptics who would discard out of hand what seems to be a remarkable achievement for the sixth century BC.
The two well-known but controversial claims of eclipse prediction in the ancient world have quite different futures. Without any written records, research on the Stonehenge megalith has all but petered out and is unlikely to generate much interest in the future. Writing is the essential ingredient of any kind of scholarship. On the other hand, the debate regarding the spectacular claim in classical history of Thales’ prediction of a solar eclipse has been reopened. Brilliant theorising by the Russian academician, Dmitri Panchenko, has produced a plausible explanation of a possible method used by Thales. Furthermore, the thousands of cuneiform records from Babylonian astronomers that survive on clay tablets date from hundreds of years before the Greeks. As contemporary research on cultural diffusion between ancient lands progresses, it may become clearer how Thales could have made his famous prediction. The lack of any explanation of how the prediction could have been made has hitherto been the great stumbling block for many contemporary historians. The Thales controversy can now be expected to have a lively future among science historians.