Fourteen

In the Zone

Basketball was an obsession of 5'9" Israeli-American psychologist Amos Tversky. He watched the game as a fan, and he played it with friends, aggressively. “He was a rough player,” Tversky’s wife, Barbara, told me. “He came home from a basketball game wounded. I said, ‘Basketball is not a contact sport!’ ”

As a fan, Tversky was aware of the hot hand theory. This is a belief in winning streaks, widespread among hoops players, coaches, sportscasters, and fans. But not just any winning streaks: predictive winning streaks. A player who’s made several shots in a row has the “hot hand” or is “in the zone.” He is judged more likely to make the next shot than he would be otherwise.

There is nothing illogical about the idea. It stands to reason that making baskets boosts a player’s confidence, and confidence is good. Success breeds success. The hot hand theory is ingrained in sportscaster commentary, and it influences court strategy. Players try to pass the ball to a teammate with the hot hand, reasoning that he will have a better chance of scoring. The opposing team’s counterstrategy is to intercept passes to the player with the hot hand and to block his shots.

Many fans regard the hot hand theory as so self-evident that it doesn’t need any proof. Just watch the game awhile and you’ll see the hot hand. Players who’ve experienced it have no doubts. Purvis Short of the Golden State Warriors once said of it:

You’re in a world all your own. It’s hard to describe. But the basket seems to be so wide. No matter what you do, you know the ball is going to go in.

Pressed for evidence, more wonkish fans can rattle off accounts of legendary winning streaks. On December 8, 1992, the Atlanta Hawks’ Dominique Wilkins made twenty-three consecutive field goals. On January 22, 2006, Kobe Bryant scored 81 points for Los Angeles against Toronto. Both are considered to be prime examples of the hot hand.

Tversky gave a seminar at Stanford in which he discussed randomness experiments. One of his students, Thomas Gilovich, suggested doing a research project about the hot hand. He felt there was a connection. Given that people are unable to produce random series, they may also have trouble understanding events that are close to random, like basketball shots. Gilovich supposed that fans exaggerated the importance of the hot hand.

“I went to talk to Amos about it,” said Gilovich, “and was surprised to find that he had an interest in it.” But Tversky insisted there was no such thing as a hot hand. It was a myth! The game was more random than fans believed.

“He said you couldn’t really test it because you couldn’t get enough data,” Gilovich recalled. “He’d gotten some small sample of data when he was spending a year at Harvard. And I said, ‘Look, I bet I can get enough data to test this idea.’ ”

To do that, Gilovich needed a complete record of hits and misses in sequence. At the time, only one NBA team had that kind of data—the Philadelphia 76ers. Their meticulous statistician Harvey Pollack supplied his records, and Gilovich’s idea evolved into a paper. Another student, Robert Vallone, was brought on to help with the statistics. Gilovich, Vallone, and Tversky published their research in a 1985 paper in Cognitive Psychology, “The Hot Hand in Basketball: On the Misperception of Random Sequences.” It ignited a controversy that’s still blazing white-hot.

This article isn’t just about basketball. It uses the sport to speak of how the mind perceives the world’s blend of predictability and randomness. The three authors analyzed the hot hand belief from many angles. They interviewed NBA players and college fans, asking whether a player who’d just scored was more likely than usual to make the next shot. Overwhelmingly, those polled said yes. The researchers examined shooting records of the 76ers and the Boston Celtics (who had free-throw data), subjecting them to extensive statistical analysis. They ran free-throw experiments with the men’s and women’s teams of Cornell University, and they let volunteers wager money on the hot hand in an economic experiment.

In all cases, evidence for the hot hand was lacking. Everyone believed (and/or bet) that he or she could predict something that was in fact unpredictable.

The article drew a crucial distinction between a hot hand and a lucky streak. It goes without saying that there are cases where a player makes an unusually large number of consecutive shots through, for lack of a better word, luck. There are likewise lucky streaks in roulette, dice, and the lottery. Reasonable people agree that roulette streaks are not predictive because roulette is pure luck.

The psychologists drew an equally important distinction between a hot hand and talent. Obviously, some players are better at making baskets than others. A good shooter is more likely to have a string of baskets than a weak one. Julius Erving, a star player at the time of the study, made about 52 percent of his shots in the 1980–81 season. You might then compare his record to the result of tossing a biased coin that has a 52 percent chance of heads. Did Dr. J have more or longer winning streaks than such a coin would have, with sequences of heads? If so, that would support the hot hand theory. Otherwise, it would suggest that Erving’s winning streaks were only those to be expected from the usual operation of chance.

The research found the latter. A player’s talent determined the overall probability of making baskets, but otherwise, winning streaks were no longer than to be expected by chance.

It’s conceivable that an opposing team’s players put more effort into blocking a winning player because they believe in the hot hand. This could erase the evidence for a hot hand—which might nonetheless be real. To test that possibility, Gilovich’s group arranged free-throw tests with Cornell’s basketball teams. There was no opposing team and no strategizing to confuse matters. It was the cleanest test of the hot hand theory, and the results were the same. The hot hand was an illusion.

Celtics coach Red Auerbach was famous for predicting victories midgame. When he felt the Celtics were on an unbeatable hot streak, he would light up a cigar. Told of the hot hand paper, Auerbach asked, “Who is this guy? So he makes a study. I couldn’t care less.”

“There are so many variables involved in shooting the basketball,” said Indiana Hoosiers coach Bobby Knight, “that a paper like this really doesn’t mean anything.”

NCAA broadcaster Billy Packer suggested, “Please tell the stat man to get a life.”

The hot hand theory has since been poked and prodded in the psychological and statistical literature; in basketball blogs, sports bars, and occasionally the general media. Scores of studies have supported and built upon GVT (the inevitable abbreviation for Gilovich, Vallone, and Tversky). A 2011 article by Tal Neiman and Yonatan Loewenstein, both of the Hebrew University of Jerusalem, looked at field goal attempts in the NBA and WNBA. The player attempting a field goal can try for an easier shot worth two points or a harder one worth three points. The decision is one measure of the player’s confidence. The study showed that pro ballers who made a successful three-point field goal were more likely to attempt a three-point goal the next time around. This would indicate a hot hand belief. Kobe Bryant, in his 2007–08 season as Most Valuable Player, was almost four times more likely to choose a three-point field goal immediately after a successful one.

But Bryant, and most everyone else, was making an error, going by the outcomes of those decisions. Neiman and Loewenstein showed that players were slightly less likely to make the shot after a successful three-point shot. The chances were 36 percent after a success versus 38 percent after a failure.

The researchers also found that players have short memories. The decision whether to attempt a three-point goal was based primarily on the outcome of the player’s last field goal (going by the observed statistics). The field goal before that had less influence, and everything still earlier was virtually forgotten as far as the present decision was concerned. NBA players’ field goal choices were about as easy to predict as those of people playing the outguessing machine.

Hot hand perceptions (and refutations) exist in many other sports. Since not all sports achievements involve a hand, the term streakiness is used. There are perceptions of greater-than-chance winning and losing streaks in baseball, football, tennis, and golf; seemingly in any sport where stats are kept. Streaks apply to teams as well as players, and to winning games and seasons, and are not limited to humans—there are streaks in horse racing and dog racing, too.

It’s now clear that the hot hand is not always a myth. An authentic hot hand seems to exist in bowling. The bowler who makes a strike gets ten points plus the value of the next two rolls. This motivates players to try extra hard after a strike, and it works. There is solid data showing that bowlers who score a strike are a bit more likely to follow it up with another strike or spare.

There is also evidence of streakiness in certain tournaments. Winning a tennis match requires winning two out of three sets. A player who wins the first set can do a full-court press (so to speak) to clinch the prize on the second. The same goes for pro golfers who are a game or two away from qualifying for a lucrative championship tour. These authentic hot hand effects exist in individual sports where the scoring system rewards consecutive wins. Team sports are usually more random, as there are so many variables beyond an individual’s control.

That doesn’t change the fact that fans are hardwired to see streakiness where none exists. Thanks to its viral propagation on the Internet, belief in the hot hand is probably stronger than ever. Impassioned bloggers still rage against Gilovich, Vallone, and Tversky’s decades-old paper. “When your whole life is telling you one thing and you directly experience it, and then you’re told the opposite, you’re going to resist it,” said Gilovich. “I don’t mean to suggest that people who believe in the hot hand are flat-earthers, but when people first said the earth isn’t flat, that seemed crazy.”

The hot hand is a consequence of the misunderstanding of chance revealed in randomness experiments. In fact, Gilovich’s group did a novel type of randomness experiment. They showed people strings of Xs and Os and asked them to say whether they looked random or not. The cover story was that these Xs and Os represented successful shots and misses in basketball. This encouraged the participants to treat the sequences as real-world data.

To give you the flavor of it, I’ll show you a string of black and white squares (easier to take in at a glance than letters). Imagine that the black squares represent a player’s successful shots and the white ones his misses, arrayed on a horizontal time line.

In the 1985 study, most people agreed that sequences like this are random.

No surprise there—except that they were wrong. Here’s what a random sequence really looks like:

It has fewer alternations of black and white, and longer sequences of the same color, than the first diagram.

The essence of randomness is unpredictability. If you can’t guess what comes next, and neither can anyone else, it’s random. The paradigm of randomness is a coin toss. You can think of the second diagram above as the result of tossing a fair coin fifty times, with the results displayed as black squares for heads and white for tails. The chance of a white square being followed by a black square (or vice versa) is 50 percent.

But when Gilovich’s team showed people this random sequence, only 32 percent classified it as due to chance. Most believed that the same-symbol streaks were too long to be just coincidence. This implies that the hot hand is not just a sports myth but a universal illusion.

The psychologists tested sequences in which the chance of alternation was 40, 50, 60, 70, 80, and 90 percent. The perception of randomness was greatest when the alternation rate was 70 or 80 percent. In the first such diagram above, it’s 75 percent, meaning that that’s the chance that a white square will be followed by a black square, or vice versa.

Only when the alternation probability was increased to 90 percent did most people recognize that the back-and-forth was too consistent to be random. Here’s an example of a sequence with a 90 percent alternation rate:

This is an almost-perfect black-white-black-white sequence. There are just two same-color strings, and they’re only two squares in length.

Once again, magicians were using these ideas before psychologists wrote about them. Illusionists have long known that an honestly shuffled deck of cards runs the risk of not appearing random to the audience. There will usually be “suspicious” clusters of similar cards, like four face cards in a row. A statistician would expect that, but average folks don’t.

Certain illusions use a stacked deck that looks more shuffled than a shuffled deck does. This is a counterpart, in cards, to the overalternating sequences that were perceived as random. In the so-called Si Stebbins arrangement, the cards alternate black-red-black-red-black-red in perfect lockstep. The suits run clubs-hearts-spades-diamonds throughout the deck. The values run A-4-7-10-K-3-6-9-Q-2-5-8-J. These patterns may sound like they would stick out like a sore thumb. They don’t. The deck just looks random.

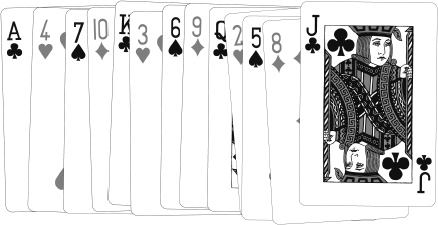
The Stebbins arrangement is easily memorized, and that’s the point. A performer who glimpses the bottom card of a cut can instantly deduce the card below it… which becomes the top card of the restored and squared-up deck. He can, if desired, name that card and every other card in the deck.

For the most part we are more than capable of fooling ourselves. Once you understand the hot hand illusion, you see examples of it everywhere. Many iPod users complain that the shuffle play feature isn’t random, can’t be random. It just played four Lil Wayne songs in a row! Streaks like that are to be expected. The bug isn’t in the software but in our heads.

The Manhattan bus schedule means little on busy corners, where traffic and lights cause buses to arrive in an approximation of randomness. Yet it doesn’t seem random at all. It seems like you wait twenty minutes for a bus, then two or three arrive in tandem.

Cognitive scientist Steven Pinker tells of an experiment in which volunteers had to press a button whenever they heard a beep. The subjects knew the beeps were supposed to occur randomly in time. They complained that the machine was broken: “The beeps are coming in bursts. They sound like this: ‘beepbeepbeepbeepbeep… beep… beepbeep… beepitybeepitybeepbeepbeep.” Explained Pinker, “They didn’t appreciate that that’s what randomness sounds like.”

When the hot hand plays out in two or three dimensions of space rather than one of time, it is known as the illusion of clustering. During the London Blitz, rumor had it that the German bombs spared the neighborhoods of Nazi spies. Maps showed clusters of hits in certain neighborhoods and none in others. British intelligence took these rumors seriously enough to divide a map of London into squares and painstakingly count the bomb hits. They concluded that the bombs were indeed striking at random. Statistician William Feller remarked, “To the untrained eye, randomness appears as regularity or tendency to cluster.” Many refused to believe it. As Chico Marx asked, “Who are you going to believe, me or your own eyes?”

Belief in the hot hand might seem to conflict with the better-known “gambler’s fallacy.” In the casino of Monte Carlo on August 18, 1913, “black” came up twenty-six times in a row. After about fifteen spins of black, word spread through the casino. Gamblers threw down cards and dice to mob the enchanted roulette table. Most wanted to bet on red. They believed that after so many blacks, red was due and stood a greater-than-usual chance. When this belief was proven wrong—as another, and another spin came up black—many doubled down, convinced that red was all the more likely on the next spin. The casino raked in millions of francs from the unusual run.

The gambler’s fallacy is the belief that chance outcomes that haven’t occurred in the recent past are more likely to occur in the near future. It’s called a fallacy for a reason. (“I’m overdue for a win!” thinks every loser.) The gambler’s fallacy incentivizes losers to keep on playing and to not learn from experience. Were gamblers endowed only with the survival instinct of rats in mazes, they would catch on that nothing good happens when I play this game. Instead, they keep on playing and may up the ante in reaction to losses. Unfortunately, roulette wheels have no way of knowing that they’re due for a win. The odds remain the same, stacked against the player.

By this point you may be confused. It sounds like I’m saying that people believe that random winning streaks will continue… except when they believe the complete opposite. The gambler’s fallacy and the hot hand theory are really two sides of the same coin. Both are consequences of the “law of small numbers.”

That is a semifacetious rule proposed in 1971 by Amos Tversky and Daniel Kahneman. It runs,

People’s intuitions about random sampling appear to satisfy the law of small numbers, which asserts that the law of large numbers applies to small numbers as well.

To understand the point, and the verbal wit, you need to know what the “law of large numbers” is. It’s one of the most fundamental rules of probability. When I toss a fair coin a few times, I don’t necessarily get an even split of heads and tails. That would be asking too much of a random process. When I toss the coin a very large number of times, however, the proportion of heads will approach the expected value (50 percent) ever more closely.

The law of large numbers acknowledges that very small samples can’t be expected to be representative of the process or the whole. We all know this, minus the fancy language, and sometimes we joke about it. The average American household has about 2.6 people. Not many have exactly that.

Tversky and Kahneman’s law of small numbers is a rule of psychology. It says that we unreasonably expect small samples to reflect the underlying odds. Should you toss a fair coin ten times, the math says it’s common to get a lopsided result like seven tails and three heads. Public opinion thinks otherwise. Show most people a coin that has just come up heads seven times out of ten, and they’ll tell you there’s something wrong with the coin.

No one is saying there couldn’t be something wrong with the coin. A coin that came up heads 700 times of 1,000 would be biased, to near certainty. There’s nothing suspicious about seven of ten, though, not if that’s all the data you have.

To put it another way, we expect small samples to be like reality show casts: one jock, one dumb blonde, one gay, one black, one Asian, etc. They’re supposed to “look like America.” But those so-called reality shows have to be cast that way. A random sample of the population would be demographically lopsided one way or another.

The hot hand paper presents a unified theory embracing the hot hand and the gambler’s fallacy. Gilovich, Vallone, and Tversky wrote,

A conception of chance based on representativeness, therefore, produces two related biases. First, it induces a belief that the probability of heads is greater after a long sequence of tails than after a long sequence of heads—this is the notorious gambler’s fallacy.… Second, it leads people to reject the randomness of sequences that contain the expected number of runs because even the occurrence of, say, four heads in a row—which is quite likely in a sequence of 20 tosses—makes the sequence appear nonrepresentative.

What causes people to switch between the gambler’s fallacy and the hot hand theory? When confronted with something that is understood to be mechanical and outside human control, we default to the gambler’s fallacy. When human will and agency are involved, we favor a hot hand belief.

The gambler accepts the unpredictability of the little ball skittering over the roulette wheel. He also believes in the law of small numbers. The only way to reconcile these two convictions is to imagine a Lady Luck who will put her thumb on the wheel, favoring red after a run of blacks—just to even things out. This is the gambler’s fallacy.

In contrast, the basketball fan has no reason to believe that the game is random. It’s about skill, strategy, and sports medicine (as well as luck). When a player has a long winning streak, unrepresentative of that player’s long-term average, it’s easy to believe that a mysterious hot hand is at work.

Hot hand thinking is probably more important than the gambler’s fallacy in human affairs. The gambler’s fallacy is a belief of the naïve that applies mainly to gambling equipment. More educated readers may scoff at the notion of a Lady Luck who micromanages cards and dice. The hot hand theory applies to human actions. It’s not so obvious that hot hand beliefs are wrong, in basketball or anywhere else. Gilovich didn’t know it was a misconception until he did the research. Smart people fall for the hot hand belief and base important decisions on it.

Did you hear the one about the optimist who fell off the Empire State Building? After falling fifty floors, he said, “So far, so good!”

This joke is a good introduction to the representativeness heuristic. Kahneman and Tversky coined that term to describe the tendency to believe that limited experience is representative of the big picture. (A heuristic is a mental shortcut.) The joke’s optimist does not have much experience in falling off tall buildings, yet he’s confident that his brief plunge—falling fifty stories without a scratch!—is representative of the fate that awaits him.

One day Kahneman and Tversky found themselves predicting the future careers of tots in their social circle. A fast-talking three-year-old would grow up to be an attorney, they joked. They knew they were making flippant forecasts from inadequate evidence. Despite that, they found considerable agreement on each child’s future. In analyzing this, they realized that they were simply matching stereotypes. A motormouthed kid is representative of the lawyerly stereotype, and this prompted the prediction.

What’s wrong with that? Nothing, as long as you take the prediction for what it is—a guess that is unlikely to pan out, given the huge number of possible adult occupations and the relatively small proportion of lawyers.

In an influential 1972 paper, Kahneman and Tversky argued that many of our informal estimates of probability are based on representativeness. Their method was to survey people, describing hypothetical situations and asking them to estimate probabilities. They found that people were wrong in consistent ways.

One scenario ran like this. In a certain city, every family with exactly six children was interviewed. It was found that seventy-two families had exactly six children with the birth order girl-boy-girl-boy-boy-girl (GBGBBG). Estimate how many six-children families had the birth order BGBBBB.

This may remind you of the Zenith radio experiments (a parallel that Kahneman and Tversky mention). Were girls and boys equally likely, all sixty-four possible combinations, from GGGGGG to BBBBBB, would be equally probable. A reasonable estimate for the number of BGBBBB families would therefore be the same as the given number of GBGBBG families, seventy-two. But the median guess offered was thirty. People felt that BGBBBB had to be less common than the “better-shuffled” GBGBBG. That, of course, is the intuition that guided the Zenith experiment guessing.

When presented with a difficult question, we sometimes ignore it and answer an easier one. (Watch the politicians on Sunday-morning TV shows for examples.) This tactic is most common when the answerer feels the “wrong” question has been asked and there is a greater truth to be spoken. That’s probably what was going on here. The estimators knew that birth order was random and wanted to emphasize that in their answers. They favored the well-shuffled option, as it better fit their stereotype of randomness.

The least important conclusion to draw from this is that average people are bad at math. The real message is that we all make intuitive judgments of probability. The most important are judgments involving human actions. These generally can’t be reduced to math or outsourced to an expert. Instead, we make these probability judgments largely by matching stereotypes. An athlete or a CEO with several successes in a row fits the “winner” stereotype, not the “random” or “loser” stereotypes. We feel that successes have to be significant; that a winning streak will continue.

The question remains, why are we so predictable, and so bad at predicting? It is easier to demonstrate how the mind works than to say why. One guess is that people are reproducing their faulty conception of randomness—much as the domestic dog’s bark is said to be an unsuccessful attempt to mimic human speech.

An embezzler cooking the books could avoid same-digit streaks in the mistaken belief that they wouldn’t be random. A basketball coach may believe that five baskets in a row are more statistically meaningful than they are. Doubtless people do have such thoughts.

This kind of thinking can’t be the whole story. Perceptions and intuitions, not just conscious beliefs, are wrong. Some have asked why evolution would shape our minds to make inaccurate predictions.

It’s been proposed that the representativeness heuristic has survival value after all. A splash of water, followed by a rustle in the bushes, could mean a crocodile is about to snatch the baby… or it could mean nothing at all. In this and many similar scenarios, it’s better to foresee and take action (sometimes needlessly) than to shrug off the unpredictability of life and do nothing.

One thing is certain: The human problem with randomness is deep-seated. Psychologist Lola Lopes compared it to the parable of the blind men and the elephant—with the crucial difference that “unlike the situation with elephants, no one at all has ever seen what randomness is like.”

The first half of this book dealt with the direct consequences of our inability to act randomly. Much of the time we deal with others who are playing the outguessing game themselves. We make predictions about the group’s predictions. This second-order outguessing is the basis of the markets that assign values to sports bets, real estate, stocks, and much else.

As early as 1989, behavioral economist Colin F. Camerer asked, “Does belief in the hot hand matter for economics?” He proposed that it might in inefficient markets such as labor and housing. Companies could pay too much for a “winning” CEO’s services; home buyers could overpay in the belief that a string of recent price increases will continue. Few would doubt either proposition today. In the years since, hundreds of studies have established the real-world impact of hot hand thinking. You can often beat the markets simply by betting against the hot hand. The following chapters will show you how.