The butterfly effect’s influence on weather, climate and the motions of the planets
It’s not a particularly new idea. You might even have grown up with the concept; it is written into a familiar children’s rhyme:
For want of a nail, the shoe was lost
For want of a shoe, the horse was lost
For want of a horse, the rider was lost
For want of a rider, the battle was lost
For want of a battle, the kingdom was lost
That is chaos theory, sometimes known as the “butterfly effect.” Can the lack of a single nail destabilize geopolitics? Can the flap of a butterfly’s wings result in a storm thousands of miles away? The answer is yes, and it happens all the time. Not necessarily in those exact ways, of course. The children’s rhyme is obviously a playful look at consequences. And even the butterfly was born in a throwaway comment.
Edward Lorenz, who initiated research in this field, was due to give a talk at the 1972 meeting of the American Association for the Advancement of Science, but had failed to provide a title. The meteorologist Philip Merilees, the session chair, eventually came up with something. In a paper nine years earlier, Lorenz had mentioned how a meteorologist had scorned chaos theory, pointing out that if it were correct, “one flap of a seagull’s wings could change the course of weather forever.” Merilees evidently remembered this line, and concocted a variant that has entered popular culture like few other scientific concepts. The title of Lorenz’s talk was “Does the flap of a butterfly’s wings in Brazil set off a tornado in Texas?”
The official term for the butterfly effect is “sensitive dependence on initial conditions.” The basic idea is that most systems that change over time—whether they are natural, such as weather, or artificial, such as the numerical output from a computer program—will turn out very differently if even the tiniest adjustment is made to their starting point. This simple observation has such profound consequences that it has given rise to a whole new field of research.
“Does the flap of a butterfly’s wings in Brazil set off a tornado in Texas?”
PHILIP MERILEES
The repercussions of chaos theory, as this field is known, have been felt across the whole of science. From the dynamics of the planets to the way epidemics spread through human populations, chaos theory’s influence is as wide-reaching as it is important. The entire universe is, it seems, in a state of chaos. This discovery would have come as a terrible shock to the grandly titled Pierre Simon, Marquis de Laplace. In the 18th century he had embraced the Newtonian revolution with relish. His book on the mechanisms of the universe, where he took Newton’s gravitational theory and used it to map out the movements of all the planets, was a masterpiece. A few years later, he boldly boasted of science’s power to tame every known phenomenon:
An intelligence which at a given instant knew all the forces acting in nature and the position of every object in the universe—if endowed with a brain sufficiently vast to make all necessary calculations—could describe with a single formula the motions of the largest astronomical bodies and those of the smallest atoms. To such an intelligence, nothing would be uncertain; the future, like the past, would be an open book.
Within a few decades of Laplace’s death, however, that vision had begun to unravel. It started in 1860, when the Scottish physicist James Clerk Maxwell discussed the amplification of small changes when considering what happens when molecules collide. Thirty years later, Henri Poincaré discovered that the mutual gravitational attraction of three moving objects displayed sensitive dependence on initial conditions. Then, in the 1920s, the Dutch engineer Balthasar van der Pol found chaos in the tones produced by a telephone handset connected to a vacuum tube. The electric current driving the tube occasionally triggered what we would recognize as feedback, and van der Pol was able to write down an equation to describe it.
“To such an intelligence, nothing would be uncertain; the future, like the past, would be an open book.”
PIERRE SIMON, MARQUIS DE LAPLACE
Though this equation was enormously useful to engineers trying to build vacuum tubes into electronic systems such as broadcasting equipment, the whistling itself was no more than a nuisance. In fact, various mathematicians and engineers studied the phenomenon without noting anything particularly remarkable about it. Though the story of chaos theory has involved many players, it was Edward Lorenz who really brought it to life.
Lorenz had been a weather-watcher since childhood, and spent the Second World War as a weather forecaster for the Army Air Corps. Some years later, when working as a researcher at the Massachusetts Institute of Technology, Lorenz combined meteorology with mathematics and the relatively new science of computing. He built a processor that could model a simple version of the weather. And it was here that he discovered the butterfly effect.
As with many of the most important breakthroughs in science, it happened by accident. One afternoon in 1961 Lorenz was short of time and halfway through a weather simulation on his computer. Looking through a print out of where he wanted to start, he punched in the numbers that would rerun the simulation from halfway onwards. It came out wrong—or at least wildly different from the original.
Alarmed by the apparent error, Lorenz checked what he had used as an input. He had, he noted, cut the numbers off after the third decimal place, assuming that the fine detail would make no difference. Where the computer had been using 0.506127, Lorenz had input only 0.506. It had made all the difference in the world. Lorenz had discovered the sensitive dependence on initial conditions: an unpredictability that arises through our limited knowledge.
Our rulers are not infinitely small, our actions are not infinitely smooth, our machines are not infinitely powerful. Thus every measurement we perform, and every computation carried out using those measurements, will have a small but finite error. Before Lorenz, that might have been considered to cause a problem as small as the error. But sensitive dependence on initial conditions means that, more often than not, the error will eventually be huge.
Everywhere we look we find chaos. The solar system, for instance, is chaotic because it involves the interaction of more than two bodies. As Henri Poincaré proved, while there are solutions to the equations that describe interactions between two bodies, add one more—or many more—and no exact solutions can be found. The mathematical equations describing the system simply cannot be solved.
With eight planets and a sun to consider, not to mention countless rocks, asteroids and comets, chaos reigns in the heavens. But a solar system that runs by chaos rather than clockwork does not mean we are in danger of colliding with another planet at any moment. Chaotic orbits are often “bounded,” moving in cycles that never quite repeat, but within a limited space, thus limiting the danger of collision.
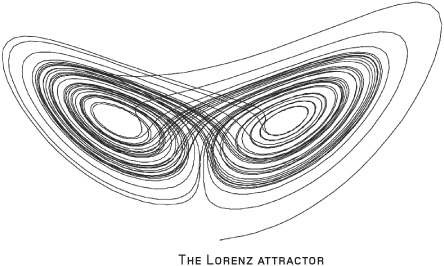
This boundedness, where chaos operates within strict limits, has given rise to another icon of chaos: the “strange attractor.” Imagine a simple system that exhibits chaotic behavior, something like a double pendulum, where two rigid rods are loosely joined and allowed to swing freely. The free movement of the double pendulum is similar to the movement of your leg from the hip, but with the knee able to bend in two directions. Until you have seen it with your own eyes, it is almost impossible to fathom the degree of unpredictability the double pendulum exhibits. It swings back and forth, with the endpoint of each oscillation seemingly at random.
Swinging freely from some arbitrary starting point, the bottom of the double pendulum traces out a pattern composed of loops that form definite shapes. Though it never makes the same loop twice, it also doesn’t deviate far from the established pattern. This “attraction” to a particular form is what gave the strange attractor its name. Perhaps the most famous example is the butterfly-shaped Lorenz attractor. This is a map of the movement of a chaotic system in three dimensions. As the motion continues, the lines are denser and denser. But the trajectory never crosses itself, and never repeats.
A similar pattern emerges from a steel pendulum set in motion just above three magnets laid out as the corners of a triangle. Each magnet exerts a pull on the steel bob, and the pull varies as the bob moves in and out of the magnet’s field. The sum of all the competing pulls forces the pendulum into a chaotic trajectory that is sensitive to the tiniest variation in its initial position or velocity. This is illustrated in its strange attractor.
The fact that these chaotic orbits are bounded does not mean they can’t have extreme consequences. This is demonstrated in the effects that the planets can have on each other. Though the orbits themselves do not stray too far from their expected paths, the chaotic motions might occasionally create a cataclysmic threat. Calculations show that a tiny kick to Saturn, from the particles that compose the solar wind, for example, can turn its orbit “aperiodic.” That means it will take a slightly different path each time it goes round the sun.
It’s a scary prospect, because it opens up the possibility that Jupiter, Saturn and the Sun will align at some moment. The combined gravitational pull of this trinity is enough to pull rocks out of the asteroid belt that lies between the orbits of Mars and Jupiter, and could unleash an asteroid storm. There have been claims that such an event preceded the asteroid impact that seems to have ended the age of the dinosaurs. If that is what happened, it would not be the first time that chaos has had an impact on biology—and it was certainly not the last. The butterfly effect rules biology as surely as it rules the swing of a double pendulum.
Chaos theory has had an enormous impact on the science of ecology. The idea of populations growing in good times and thinning out in the bad times has always been a strong part of biological thinking, but the rise of chaos theory and the butterfly effect created a Eureka moment. Before chaos came along, biologists of a mathematical bent would write down equations that approximated to the situations they were interested in. They might describe, for instance, how many squirrels were living in a square mile, how rich their food source was, how frequently they reproduced, and how many predators shared the territory.
From that, they could work out how that population of squirrels would grow and diminish over time. But any time the equations gave results that seemed to be going out of control, the mathematical biologists would “reset” the scenario, assuming that there was some instability in the system that needed to be reined in. With the advent of chaos theory, it became clear that the wild changes could quite easily be a natural part of the system.
Imagine, for instance, a population of squirrels with no predators. If, on average, each adult produces less than one offspring per generation, the population will dwindle to zero. If the number of offspring is between one and three, there is some stability. If the average number of offspring per generation is more than three, however, things get strange.
A tendency to “boom and bust” appears in the population statistics. It is, essentially, the same as that whistling valve tube in the telephone line mentioned earlier: a process of feedback creates wild oscillations. Chaos theorists call it a “bifurcation.” It means that the population is uniquely sensitive to the number of offspring per generation. In one year, the population will boom, but in the next it busts. There’s nothing in between. Then the bifurcation splits again and again, and things eventually start to look random: there is no apparent pattern. But only for a while: as time goes on, the number of offspring increases again, and, out of nowhere, another bifurcation comes into play.
Such complexity is everywhere in the natural world, and understanding it can save lives. The hit and miss, up and down, boom and bust occurs in epidemics of diseases like AIDS, measles and polio, for instance. Because the number of cases follows a chaotic trajectory, it is sensitive to a knock from something like an inoculation program. But that knock doesn’t always wipe out the disease; instead, the numbers can be thrown into an unstable regime—around a bifurcation region, for instance. This means that short-term figures for the disease might rise, suggesting that a program of inoculation has failed. Awareness of chaos allows medical researchers to see beyond the initial response, and allow for the chaotic response, mapping what is hopefully a downward trajectory over the long term.
Here’s a simple question: how long is the coastline of Britain? Look it up in a few encyclopedias, and you’ll get wildly differing answers—the difference can be as much as 20 percent. That’s because the most straightforward answer anyone can give is that it depends on the size of your ruler. Given a smaller ruler to work with, there will always be smaller features to measure. Coastlines, like myriad features of the natural world, are self-similar, or “fractal.”
As a result, you can always measure a fractal coastline more closely, and add to the total length you already have. As you zoom in on a fractal structure, the essence of your view does not change. At each size-scale, the same patterns are repeated. Given a picture showing nothing but desert sand dunes or ocean swell, for instance, you cannot tell whether you are looking at a few square kilometers or a few square centimeters. It’s the same with coastlines.
Creating a fractal is just a matter of drawing simple but repeated shapes. The Koch snowflake, for instance, is composed of triangles added to the center of each side of an existing triangle. The added triangles have side lengths one-third of the side on which they rest. After a few iterations, the result is an astonishingly detailed pattern.
This intricacy is the hallmark of fractals, and it is the point at which they relate to chaos theory. Chaos theory says that generating a perfectly accurate picture depends on starting with perfectly accurate information—which is impossible. In a chaotic system, any inaccuracies in the information are grotesquely amplified to give a badly distorted picture. Fractals are something like chaos theory turned on its head: the accuracy of the information you gain from a picture depends on how closely you are looking at it—and you can never get close enough to get perfectly accurate information.
As a result, the manifestations of fractal behavior intrigue and infuriate in equal measure. Researchers have been intrigued to find fractal structures outside of the natural world. Financial data—records of stock-market trades, for instance—often take a fractal form, suggesting that their detailed structure arises from absurdly simple rules. But inferring useful information about those rules is absurdly and frustratingly difficult.
The most famous fractal structure is the Mandelbrot set. First created by French mathematician Benoît Mandelbrot, it is defined by a relatively simple equation, but forms a complex collage of balloons, thorns, spirals and jets, all of which contain similar structures. Its aesthetic appeal is almost unparalleled in mathematics, but what does it mean?
That is still not clear. Researchers have suggested that the fractal structure of financial markets may mean that markets are governed by simple rules and are thus far easier to analyze (and thus, perhaps, predict) than one might imagine. The ubiquity of fractal structures in natural and artificial systems, and in human culture—many common musical patterns, and Jackson Pollock’s art, for example—has led Mandelbrot to claim that they are a key to unlocking deep secrets of the universe. As yet, however, the study of fractals has not produced any insights we can truly call significant.
An understanding of biological chaos and the butterfly effect is saving lives around the world in a more immediate way too. Your heart beats because of coordinated pulses of electricity that work through the cells in a kind of wave, causing the muscle to contract in specific ways and at specific times. When this breaks down, an “arrhythmia” occurs. Heart arrhythmias kill hundreds of thousands of people each year: for myriad reasons, the heart can stop beating normally—or, indeed, at all. Often the muscles are all contracting randomly, and the heart is no longer a pump, but a seething, pulsating mess of tissue. It’s a chaotic system—and one where a good kick can take the chaos away.
Medics have long known that a jolt of electricity can set this problem right again, but you can’t just put any old jolt into a human heart. To set the rhythm right again requires an understanding of its chaotic dynamics. The heart is, effectively, an oscillator like a pendulum. And when you know how a chaotic pendulum can be controlled, you can also design a defibrillator that works much better than the ones designed by trial and error. The main area where the butterfly effect has been put to work, though, is exactly where it started: the weather.
Meteorologists like to run hugely complex simulations of the Earth’s weather systems on massive supercomputers. The simulations are based on the laws of physics, and model things such as how ocean and air currents move around the globe. Before the butterfly era, we might have thought that a suitably powerful simulation would predict the weather weeks, months or maybe even years in advance. Chaos tells us this is just not possible.
The trouble is, the physics of the models is approximate, and the data used to set up the simulation even more so. The weather stations used to gather information are scattered over the Earth, with large gaps between them: we don’t have the information from the places between the weather stations. Scientists now know that, within just a few days, these sources of error are enough to set the weather models off on a trajectory that will bear no relation to what actually happens to the weather. A butterfly flapping its wings somewhere between the weather stations could cause a storm that no one saw coming.
Of course, the meteorologists reset their models every time they get new data in. They also run “ensemble” forecasts, where they put slightly different initial conditions into the model and look at how much the outcome varies. That allows them to create an averaged forecast that is likely to be more accurate than any one prediction. It also allows a measure of the reliability of their forecast. It’s not enough to have a prediction—it’s better to have an idea of how much you should trust that prediction.
Ironically, the longest-term predictions come out OK: the science of climate prediction is not so sensitive to initial conditions as are short-term weather predictions. That’s essentially because climate prediction deals more in generalities than specifics. The flap of a butterfly’s wings might cause a storm in Texas, but another flap might calm a storm that was already blowing up. Over the 30-year average that constitutes a climate analysis, the number of storms evens out, and each butterfly becomes irrelevant.
Lorenz used the equations of chaos theory to show this. When you look at a strange attractor, you see a particular shape. Applied to climate science, the shape you see indicates the future climate. The flowing line that moves around unpredictably, gradually creating the shape, is like noise on the signal; it is not the parameter of interest. That means running climate simulations, however chaotic their predictions might be over the short term, reveals a reliable broad-brush picture of what is coming. So, does chaos theory spell disaster? Quite the opposite: that flapping butterfly has been instrumental in warning us about the greatest threat faced by humanity: runaway climate change induced by human activity. Chaos is not always a problem.