David Konstan

Epicurus on the Void

1 Introduction

In this paper, I investigate several aspects of the Epicurean conception of space and its properties. First and foremost, I argue that Epicurus conceived of space as the complement of matter: that is, space is where matter is not. This view is not new: it was articulated, indeed, in the nineteenth century,176 but the combined authority of Carlo Giussani and Cyril Bailey succeeded in displacing it with another interpretation, according to which space is a continuous matrix that extends uniformly throughout the universe, and is either filled, when it is occupied by matter, or empty, when matter is absent.¹⁷⁷ In a learned and subtle paper, Brad Inwood ably defended the earlier view, and demonstrated, furthermore, that Epicurus was indebted to Aristotle’s ideas about space and place, even as he departed from Aristotle in insisting on the reality of void, which Aristotle had denied.178 However, in an important article that appeared at almost the same time as Inwood’s, David Sedley reaffirmed, with new arguments, the view of Giussani and Bailey.¹⁷⁹ Sedley restated his interpretation in the influential collection of fragments of Hellenistic philosophy that he edited together with Anthony Long, and it soon became the new orthodoxy, accepted largely without question by most scholars thereafter.¹⁸⁰ But Sedley’s argument was, I believe, not entirely cogent, and I hope to show here, using a somewhat different line of reasoning, that Inwood’s interpretation is in fact true to Epicurus’ conception.

Space, according to Epicurus, also had the property of being constituted out of minima; that is to say, minima were not only the smallest and inseparable constituents of atoms but also the smallest conceivable units of motion through the void. I argue that space did not, however, serve the function of separating atoms from each other, as some have supposed, nor is the directionality of the universe (that is, the fact that atoms tend to move downward) due to a property of space itself (it is a consequence rather of the fact that the atoms have weight). Space did, however, on Epicurus’ conception, serve as what would later be called an absolute frame of reference, in respect to which atoms move; space changes shape internally but taken as a whole it stands still. Finally, I argue that space was not strictly passive but entered into the constitution of compound bodies, in so far as their density is a function of the relative proportions of matter and void.

2 Bodies and Space

According to the Placita Philosophorum ascribed to Plutarch (877d-e), Epicurus maintained that “the principles of existing things are bodies that are observable by reason, without a share of void, ungenerated, eternal, and indestructible” (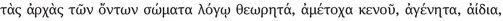 ἄφθαρτα; cf. Aët. 1, 3, 18, p. 285 Diels = fr. 267 Us.). The atoms cannot be altered or crushed, but “they move in the void and through the void; the void itself is limitless and the atoms are limitless [ἄπειρα]”, i.e., in number. The passage adds that “the following three things are attributed to bodies: shape, size, and weight. Democritus mentioned two, size and shape, but Epicurus added a third to these, namely weight. For it is necessary, he said, that bodies move by the blow of weight [ 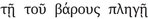], since otherwise they will not move”. I will return to weight later; here, we may note simply that the two attributes of bodies that Epicurus inherited from Democritus (according to this source) would seem to be equally applicable to the void. If this were all that pertained essentially to bodies, then space would appear to be indistinguishable from matter, as Descartes argued in the Principles of Philosophy (1644), Part 2, Section 11: After mentally rejecting “all that is not essential to the nature of body”, Descartes writes, “we will find that nothing remains in the idea of body, except that it is something extended in length, breadth, and depth; and this something is comprised in our idea of space, not only of that which is full of body, but even of what is called void space”.181

I believe, however, that Epicurus’ formula in fact prevents the collapse of body and space into a single substance characterized by extension. For one thing, Epicurus speaks here not of ‘body’ but of ‘bodies’: the plural is not applicable to space. Bodies indeed are marked by shape and size, but this pair is not simply reducible to the idea of extension, as Descartes supposed. For Epicurus evidently means that bodies have a specific shape and size: this is what it means to say that “they are not susceptible to being crushed [θραυσθῆναι] or to undergoing formation out of parts or to being transformed [ἀλλοιωθῆναι]”. It is true, of course, that bodies are subject to rotation, but their geometrical outline is invariable: a triangular atom cannot become circular. But this is not true of space, at least of space conceived of as the empty region that is unoccupied by atoms, as opposed to the extended matrix in which atoms are presumed to be located, which includes the space they occupy. When atoms move, the space between them is reconfigured: this is enough to discriminate between bodies and space.

It is important to bear in mind that Epicurus does not posit as his two fundamental principles body in the sense of matter and void, but rather bodies and void. This point is sometimes missed or overlooked by commentators. Thus, in their excellent compilation of Hellenistic philosophical texts, Long and Sedley translate Epicurus’ Letter to Herodotus 39–40 as follows: “Moreover, the totality of things is bodies and void […]. Beyond these [i. e. body and void] nothing can even be thought of ”.¹⁸² But Epicurus never speaks of ‘body’ in the sense of matter as such, or what Aristotle called 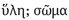in the singular always refers to a particular body.183 Lucretius, it is true, writes (1, 419–423):

omnis ut est igitur per se natura duabus
constitit in rebus; nam corpora sunt et inane,
haec in quo sita sunt et qua diversa moventur.
Corpus enim per se communis dedicat esse
sensus.

Long and Sedley would seem to be rendering this passage literally when they translate: “The totality of things, then, in so far as it exists per se, has a nature made up out of two things: there are bodies, and void in which these are located and through which they move in their various directions. That body exists is declared by universal sensation itself”.184 But I am inclined to think that corpus should be taken here to mean ‘a body’ (and by the way, I would attach per se in the Latin to corpus, not to communis sensus); the meaning is: “Universal sensation affirms that a body exists per se”. Sensation is not assumed to verify something as abstract as matter (or even atoms, which are beneath the threshold of sensation). This is clear too from the passage in the Letter to Herodotus which corresponds to Lucretius’ verses (and also, according to a scholium, to what Epicurus stated at the beginning of the Great Epitome and in the first book of On Nature): “that there are bodies, sensation itself bears witness in all instances” (Ep. Hdt. 39: 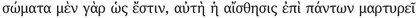); this is, I think, closer to Epicurus’ meaning than Long and Sedley’s version: “That bodies exist is universally witnessed by sensation itself”.¹⁸⁵

Lucretius goes on to say (1, 426–428):

tum porro locus ac spatium, quod inane vocamus,
si nullum foret, haut usquam sita corpora possent
esse neque omnino quoquam diversa meare.

if place and room, which we call ‘void’, did not exist, bodies could not be located anywhere, nor have anywhere at all to move to in various directions.

The reference is again to bodies, not to bare corporeal matter. Now, Lucretius’ language might suggest that he is including, under the term ‘void’ (inane, which renders κενόν), two different notions: on the one hand, what we might call ‘place’ (locus, which renders τόπος), and, on the other hand, something like ‘space proper’ (spatium). It is tempting to think here of the distinction between space conceived of as a universal matrix, extending uniformly and infinitely in all directions as a limitless substrate, and what we might call empty space, that is, the interstices between bodies. But this runs counter to the corresponding passage in Epicurus’ Letter to Herodotus (40). To be sure, Long and Sedley render the latter passage as follows: “if place, which we call ‘void,’ ‘room’, and ‘intangible substance,’ did not exist, bodies would not have anywhere to be or to move through in the way they are observed to move”.¹⁸⁶ But ‘place’ here derives from a dubious emendation proposed by Usener in the preceding sentence. The text of Diogenes Laërtius is vexed; Arrighetti reads as follows:

The insertion 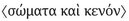goes back to Gassendi, and is surely the most obvious supplement and accepted by a majority of editors. Long and Sedley, however, adopt the emendation of Usener, who supplied 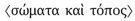. The motive for this alteration comes at the end of this sentence and the beginning of the next, where Usener reads: 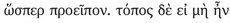, etc., which Long and Sedley again follow. The correction of τὸ πρόσθεν to τόπος δέ is paleographically clever, but philosophically implausible.187 Rendering the text that the majority of editors accept gives: “if there did not exist what we call ‘void,’ ‘space’ [χώρα here corresponding to Lucretius’ spatium], and ‘intangible nature’, bodies would not have anywhere to be or to move through in the way they are observed to move”.

Now, in a way the choice between κενόν and τόπος should not matter very much.¹⁸⁸ If, as we are assured by various sources (e. g., Aët. 1, 20, 2), not to mention this very passage in the Letter to Herodotus, Epicurus entertained only one notion of void, which is called by various names, then the substitution of locus for κενόν in Lucretius’ verses would hardly make a difference. There is some evidence, moreover, that Epicurus himself may have used τόπος instead of κενόν in identifying the two elementary principles of nature.¹⁸⁹ Sedley indeed affirms: “I understand Epicurus’ wording (at Ep. Hdt. 40) “place’, which we call ‘void’, ‘room’ and ‘intangible substance”, as an announcement that he will use its various names indifferently […]. True to his word, he does elsewhere fluctuate in his usage”.¹⁹⁰

The danger in adopting Usener’s emendation derives not so much from the substitution as such as from the associations attaching to the term τόπος, which may – but need not – suggest an extension that is filled with a body, as opposed to empty space, that is, κενόν, as though 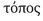and κενόν were, after all, in some fashion distinct. Thus, after rehearsing Aristotle’s critique of void, Sedley concludes: “the only available move short of abandoning void altogether is to allow that void does after all remain when a body enters it. But the only way in which it could coexist with a body would be by becoming that body’s place. Hence Epicurus has no choice but to follow Aristotle’s lead in conflating void with place”¹⁹¹ – as opposed, that is, to seeing ‘place’ as a mere synonym for ‘void’ in the sense of the absence of matter.

To which notion, then, does Epicurus’ ‘void’ correspond – that of the uniform matrix or that of interstitial space, the region between bodies? The answer must, I think, be the latter. Our sources agree that bodies are either situated in space (as Lucretius puts it) or move in and through it (as pseudo-Plutarch has it). To be ‘in space’ does not mean to be superimposed on an ostensible substratum but to be surrounded by space. Whatever Epicurus may have thought of the Aristotelian definition of place as the inner boundary of the surrounding container (see further below, p. 89), the image he conjures up is that of a stone in water or air: space is circumambient. The testimony of Sextus Empiricus (M 10, 2) might seem to tell against this view:

Sextus is asserting here that what Epicurus calls “the intangible nature” is “dubbed κενόν, τόπος, and 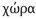” in accord with different perspectives or mental attention (διαφόρους ἐπιβολάς):

for the same nature, when it is in a state of being empty of all body, is labelled κενόν, but when it is occupied [καταλαμβανομένη] by a body is called τόπος, and when bodies are moving [χωρούντων] through it becomes χώρα. But it is collectively spoken of as ‘intangible nature’ by Epicurus because it is deprived of touch in the sense of resistance [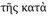 ἀντίβασιν ἁφῆς].192

Sedley, who calls special attention to this passage, comments:

Epicurus invents the technical expression ‘intangible substance’ for space in its broadest sense, whether occupied or unoccupied. He then explains the familiar words ‘void,’ ‘place’ and ‘room’ as being merely the terms by which we refer to it in specific contexts: ‘void’ when it is unoccupied, ‘place’ when it is occupied, and ‘room’ when bodies move through it.¹⁹³

Now, there is no evidence that Epicurus ever used 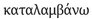in the sense of ‘occupy’; moreover, he does not typically use τόπος in the sense of ‘location’ but rather in the sense of ‘locale,’ ‘spot,’ or ‘site’¹⁹⁴. Thus, a body may arrive simultaneously at many places (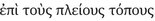, Ep. Hdt. 47), or again in reference to a point of departure (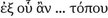, ibid.). Again, he speaks of objects arriving at places above our heads ( 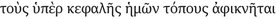, 60) or of atoms being borne toward a spot (ἐφ᾽ ἕνα τόπον φέρεσθαι) inside a compound (62), or more prosaically, of places where different peoples dwell (ἡ 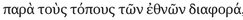, 75). A place is something to be left behind or reached; Epicurus does not use the term to indicate where a thing happens to be.195 Thus, Sextus’ clever paradoxes (M 10, 20–23) about what happens to space when an object comes to occupy it do not necessarily controvert Epicurus’ conception. Space, in the sense of void, simply changes its configuration when bodies move within it; it is always and only where bodies are not.

I must depart also, and for the same reason, from Keimpe Algra’s interpretation of Epicurus’ position: “there is really only one kind of spatial extension (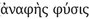), which is strictly speaking only to be called void, when it is unoccupied. As soon as such a void is occupied by a body, it ceases ipso facto to be void in that strict sense and becomes the place (τόπος) of the body”.¹⁹⁶ Algra has to concede that “This is not to say that Epicurus remained faithful to his own conceptual distinctions in practice”;¹⁹⁷ thus, in Ep. Hdt. 44, where Epicurus speaks of the void as separating atoms, κενόν means, as Algra observes, ‘unoccupied space’ and so too at Ep. Pyth. 89, where Epicurus speaks of “a region with many void spaces”.198 Algra does, however, offer another passage in support of his view that more than one type of void is at least implicit in Epicurus’ treatment, namely Ep. Hdt. 41–42, where Epicurus argues for the infinite extent of the universe (“if the void were finite, the infinite bodies would not have anywhere to be”).¹⁹⁹ Algra comments: “The wording leaves no room for doubt; the conception of void here used is … that in which bodies are and through which they move, i. e. space tout court” since “Epicurus did not mean to argue that there is an infinite amount of empty space”.²⁰⁰ A look at the larger context in which Epicurus makes this statement, however, suggests that Epicurus was indeed maintaining that empty space, that is, the κενόν, is infinitely extended:

The initial proposition is that the whole (that is, τὸ πᾶν) is infinite, since it has no limit (πέρας). Within the whole, bodies are infinite in number and void is infinite in extension. Bodies and void are complementary constituents of the whole. Both must be infinite (in different respects), since if the void were infinite in extension but bodies finite in number, bodies would be scattered throughout the infinitely extended void and hence could not collide and form compounds, as we see they do. If, in turn, the void were bounded, then the infinite bodies would not have anywhere within which they could stand (ἐνέστη: note the prefix), so as to be surrounded by space – as they must be if there is to be motion at all. The proportion of bodies and void changes as bodies enter or depart from any bounded region: add more bodies and the quantity of void diminishes. Epicurus’ point is that the void cannot shrink to zero, as it would have to if void were limited but bodies infinite in number, since bodies are always in, and separated by, void.

So far, I have been considering the Epicurean conception of space in purely geometrical terms: space is extended, and at any given moment may be said to have shape and size (the latter being infinite), but the shape changes as bodies move through it. Thus, the motion of bodies in space is in fact crucial to defining space itself: if bodies did not move, space might well be regarded as a single, huge body – though even in this case, it would differ from bodies in that bodies are bounded, and space is not; to put it differently, bodies are in space, but space is not in bodies. The distinction may be made clearer by observing that one can theoretically draw a line from any point in space to any other, without traversing the boundary of a body; the reverse, however, is not the case: one cannot draw a line from the inside of one body to the inside of another without crossing their boundaries. Space is continuous (I am assuming that atoms cannot coalesce to form a solid container around a portion of void; atoms continually collide with each other in compounds, careening in various directions, and do not form a solid phalanx).201

Epicurus did, however, have something more to say about the nature of space, namely, that it is, in contrast to body, intangible. This is what permits bodies to move through it; when they encounter other bodies, they are blocked, since they cannot penetrate them (at the microscopic level, atoms must move off in some other direction, since they cannot stand still in Epicurean theory but move continually at a very fast and uniform speed). The intangibility of space means simply that space offers no resistance to bodies in motion, whereas bodies do. Sextus is quite right to define touch in relation to resistance or ἀντίβασις, although this term is not found, I think, in Epicurus himself. It is not just that space permits motion, as Epicurus argued, as against the Aristotelian supposition of a kind of sliding interchange of places in a plenum, though this is of course a crucial part of Epicurus’ argument for the existence of void; put the other way around, the fact of motion is the condition for the concept of void. Motion is just the rearrangement of positions, in which the shape and size of bodies are invariant whereas the contours of space are altered. The intangibility of space is Epicurus’ name for its susceptibility to such alteration, just as the tangibility of bodies is manifested in their resistance to any form of change, save that of position.

It is natural today to contrast the Atomists’ view of space sharply with that of Aristotle: for Aristotle, writing in the tradition of Plato and going back ultimately to radical insights of Parmenides, a void was tantamount to nothingness, and nothing, by definition, does not exist; hence, there can be no void, and the universe is a plenum (Aristotle of course advances special arguments of his own to support this conclusion, such as the absence of natural places in a void, the necessity that objects move at an infinite velocity in a void, and so forth). But rather than reject the reality of motion altogether, in the manner of the Eleatics, Aristotle argued that motion is possible even in a universe full of matter, since objects could slip by each other as we all do in the surrounding air.202 Inwood cites Aristotle’s Physics (216bl7–20): “For air is something real, but does not seem so – neither would water, if fish were made of iron. For touch provides the test for what is tangible”.²⁰³ And Inwood adds: “Fish moving through water could, if the proportions were right, find fluid water to be as void-like as we find air. This recalls Lucretius’ use of the fish example. If the analogy is extended from water to air to an ideal fluid yielding to atoms, which are perfectly solid bodies …, then motion in a void is conceivable by empirical analogy”.²⁰⁴ Thus, Epicurus made good Democritus’ failure to explain just how motion was possible in a void: “This yielding, identical to void’s lack of resistance and intangibility …, was conceived as analogous to the yielding of fluids to objects on the phenomenal level. The problems raised by 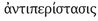on the phenomenal level do not arise for the ideal fluid, void”.²⁰⁵

To conclude: it is not the case that Epicurus coined “the technical expression ‘intangible substance’ for space in its broadest sense, whether occupied or unoccupied”, as Sedley has it; space is never occupied, but is simply the complement of atoms, existing where they are not. The point seems to be expressed with exemplary clarity by Lucretius (1, 503–510):

Principio quoniam duplex natura duarum
dissimilis rerum longe constare repertast,
corporis atque loci, res in quo quaeque geruntur,
esse utramque sibi per se puramque necessest.
Nam qua cumque vacat spatium, quod inane vocamus,
corpus ea non est; qua porro cumque tenet se
corpus, ea vacuum nequaquam constat inane.
Sunt igitur solida ac sine inani corpora prima.²⁰⁶

It was radical enough on Epicurus’ part to have posited as an elementary principle of nature an entity that has no resistance, and whose property it is simply not to impede the movement of bodies – call it what you will. This is what he needed to counter Aristotle’s objections. From the vantage point of modern physics, it may seem almost inconceivable that an Atomist did not take the extra step of envisaging the void as a universally extended and unchanging substratum that was either occupied by matter or empty. But Epicurus was not thinking of matter versus void but of bodies as opposed to the absence of bodies, and his conception of space conforms perfectly well to this vision.

3 Minima

We have now established what we may call the moving geometry of space, but there is still more to be said about its structure at the microscopic level. As I have mentioned, Epicurus held that atoms, the smallest bodies which are inalterable because they possess no admixture of space, all move at an equal speed through the void (the doctrine of ἰσοτάχεια; the abstract noun is found first in Simp. Ph. 10, 1019, 23); when atoms are entangled in groups, they vibrate in the confined spaces with no loss of velocity.207 The reason for this uniform motion of atoms has to do, I believe, with the doctrine of minimal parts: atoms proceed at a rate of one minimum of space per minimum of time. I realize that there is some controversy over whether Epicurus himself expounded the thesis of spatial and temporal minima, and if so, just when in his career; however, there can be no doubt that later writers, including Sextus Empiricus, regarded the granular or quantum nature of space and time as a feature of Epicurean physics, and I see no good reason to suppose that it was a later development. This is not to say that space is composed of minima, any more than atoms are: there are no free-standing minima, and if there were they could not be assembled into a continuous interval, since they have no parts and would, if placed adjacent to one another, wholly overlap in the way that Aristotle demonstrated must be the case for mathematical points. But motion in space is saltatory, as Simplicius makes clear 208 and as the conundrum posed to Epicureanism by Sextus (M 10, 144–147) presupposes. Sextus invites his readers to think of two atoms separated from each other by nine minima, and heading straight at one another at identical velocities, in accord with ἰσοτάχεια. After one temporal minimum, he observes, they will be seven spatial minima apart: Sextus clearly assumes that atoms travel exactly one minimum of space per minimum of time. In successive temporal instants, the atoms will be five minima, three minima, and finally just one spatial minimum from one another. And here is the puzzle: the atoms cannot meet in the middle of the minimum, because minima are partless; nor can one atom cross the minimum while the other stands still, since this would violate the principle of ἰσοτάχεια. As a result, the atoms cannot meet or rebound as the result of a collision. Now, I believe both that this puzzle must have had some basis in the Epicurean theory of minima, and that the Epicureans in fact had an answer to it. What this answer was is beyond the scope of this paper; suffice it to say that Epicurean minima are infinitesimals – the inverse, I maintain, of the magnitude that Epicurus called “incomprehensible but not strictly infinite” – and with infinitesimals it makes no sense to speak of an odd or even number of them, any more than with incomprehensibly large quantities.²⁰⁹ For present purposes, the salient point is that spatial intervals, like those within an atom, are not continuous but quantized. This must be a property of the void, if Sextus’ puzzle is to make any sense.

4 Does Space Separate Atoms?

So far, we have observed that space is rearranged as atoms move in it, and that it is granular in structure, in this respect like bodies. But does space have a more active role to play in Epicurean physics, apart from being where bodies are not? One possible function is that of keeping atomic bodies separate, so that they do not fuse with one another upon contact. The idea was proposed for Democritus, at all events, by Philoponus, in his commentary on Aristotle’s De generatione et corruptione: “Democritus did not speak precisely of contact when he said that the atoms are in contact with one another […] but rather what he called contact was the atoms being near one another and not standing very far apart” (1, 8, p. 158 = frr. 236–237 Luria). Salomo Luria 210 was persuaded that this was in fact Democritus’ view, and it has recently been adopted by Charles Taylor in his commentary on Democritus. Taylor writes: “Hence what appears to be impact [between atoms] is in fact action at an extremely short distance; rather than actually banging into one another, atoms have to be conceived as repelling one another by some sort of force transmitted through the void”.²¹¹ There is, however, no evidence whatsoever for appeal to such a force by Democritus or any other Atomist, and whatever the basis for Philoponus’ statement, it cannot be this.²¹² In discussing the oscillatory motion of atoms trapped in compounds, Epicurus remarks: “For the nature of the void which delimits [διορίζουσα] each atom provides this [i. e., the possibility of moving], since it is unable to offer resistance [ὑπέρεισις]; and the solidity which belongs to them makes the rebound in the case of collision [σύγκρουσις], to whatever distance the entanglement allows the separation from the collision” (Ep. Hdt. 44). Space indeed surrounds any atom and enables it to move, up until it makes contact with another, at which point it takes off in some other, unblocked direction; but there is no suggestion that an interval of space, however small, continues to mark off the atoms as they meet, and thereby prevents full contact. We can, however, make a guess at the problem that Philoponus’ proposition was intended to solve. If elementary bodies are nothing more than bounded shapes, then when two of them abut over some extended surface, in what way do they differ from a single body with the outline of the two combined? Why don’t they fuse? Various answers have been proposed, for example that atoms are by definition inalterable in shape, or that contact occurs only at an unextended point.213 I myself think that the doctrine of minima served to provide atoms with an edge, an outer layer of minima inseparable from each atom, and these edges preserve the integrity of atoms that are in contact. However this may be, there is no need to ascribe to space the function of preventing the fusion of adjacent atoms.

5 Does Space Have Direction?

Within the infinitely extended Epicurean universe, atoms are said to fall. If they are to fall, as opposed simply to moving randomly, it follows that there must be some privileged direction that is understood to be down. Epicurus’ universe thus has orientation. Does space somehow produce this directionality, and can ‘down’ in some sense be a quality inherent in space? Even though infinite space clearly has no bottom, is it somehow characterized by ‘downwardness’ and, presumably, ‘upwardness’? How do atoms know which way to fall? In my view, the tendency for atoms to fall is a property, not of some presumed orientation intrinsic to space, but rather of atoms themselves: it is precisely a function of weight, which, we are told, Epicurus added to shape and size as an essential characteristic of bodies.214 Now, it is obvious that not all atoms are at all times moving at uniform speed in a single direction – a kind of rain of atoms – since, as Lucretius pointed out, this would mean that there would be no collisions and hence no interactions among atoms; atoms would instead be motionless with respect to one another. Atoms evidently have some inherent tendency toward movement in a privileged direction, which they manifest without ever slowing down. How they accomplish this is not entirely clear: perhaps they start to slope a bit in the course of their flight, or else, as I have proposed, they tend to emerge from collisions asymmetrically, favouring a particular direction which is by definition down.215 I take this to be implied in pseudo-Plutarch’s statement about “the blow of weight”, though this phrase may be interpreted in other ways. However it may work, the point here is that the directionality of the all is a consequence of a property inherent in bodies, not in space.

6 Does Space Provide an Absolute Frameof Reference?

If atoms do fall, then in respect to what do they do so? If we imagine a situation in which atoms are all falling in parallel – which is conceivably the long-term result of the effect of weight in atoms, prevented only by the swerve that shifts their alignment and restarts the sequence of collisions – then with respect to each other, as I have said, they are not moving; so what is the difference between their all moving uniformly and their not moving at all? With respect to what immobile frame of reference can the atoms be said to be in motion? I raise the question, which of course has become particularly salient in modern relativity theory, in order to consider whether Epicurus may not have thought of space as somehow unmoving, and that even if there were but a single atom in the universe, it could be said to move, or to be still, with respect to the stationary medium in which it travels.216 With but one atom, or several atoms moving in parallel, one could as well speak of space moving up as of atoms moving down. But if, as I have been arguing, space is characterized by its changing contours as bodies move through it, then the effect of such complex motions on space cannot be described as a simple linear shift. It is more economical to take space as a whole to be stationary and ascribe motion to atoms, and this was plainly the way Epicurus regarded it.

7 Space and Density

There is one more possible function for space in Epicurean physics, and this has to do with the density of compound objects. David Sedley maintained that space did not have this active capacity. “Body and space are in some sense joint constituents of the world”, he allowed, “yet many parts of space are completely occupied by body”.217 Nevertheless, according to Sedley, “Epicurus was perfectly well aware that void as he conceived it was of a very different order of being from body. He resisted the temptation to follow Leucippus and Democritus in calling it an element, and used that name for atoms alone (Ep. Pyth. 86). He never makes the mistake of regarding a compound body as made out of atoms and void in combination”, in contrast to the early Atomists, who maintained, on Sedley’s view, that the void was “a substance housed in space”; thus, the void “could presumably be an element of a compound body and move around with it; but once Epicurus had identified void with place, it became stationary and no longer available as an element of movable compound bodies”.218 Sedley concluded: “Compound bodies consist of atoms variously spaced out. Space provides the location of these atoms, the intervals between them, and room for them to move; but it is not itself part of the compounds”.²¹⁹ Though I differ with Sedley in that I do not believe that space is ever “occupied by body” but is rather just where body is not, the question remains whether Epicurus conceived of space as a part of compounds, along with the atomic constituents. Some compounds are lighter than others, and this is because the sum of the volumes of the atomic components in a given volume in the lighter compound is less than that in an equivalent volume of the heavier compound. One could express this by saying that the ratio of matter to space is greater in the heavier compound, and that density is a function of the proportion of the collective atomic volume to space. Put this way, it might appear that space enters into the formula for density as a constituent principle, as it were, a co-cause of density (density, as Epicurus knew, does not make a compound fall more swiftly, but is crucial to the phenomenon of ekthlipsis or extrusion: denser objects displace more rarefied ones, driving them back with respect to the direction of motion, which will be up when the primary direction happens, as it commonly does, to be down). I see no way of eliminating reference to space in defining or describing the density of a compound, nor any need to do so: the relation between bodies and void, whether in terms of the positions and movements of the bodies in the void or their total volume in relation to that of void, is what constitutes the Epicurean universe. Space and bodies are complementary.²²⁰

8 Conclusion

Kosmoi are local regions where atoms are particularly numerous in relation to space and sufficiently entangled to create a kind of integument, so that atomic collisions in a confined space are frequent. Outside of kosmoi, atoms are fewer and can move over great distances relatively unimpeded, and so their average velocity over such distances approaches or is equal to the natural speed of atoms, which is very great (as swift as thought, as Epicurus puts it). It must be emphasized, however, that atoms do not move more slowly within kosmoi or compounds; if their linear motion is restricted by other atoms, they vibrate back and forth and so the overall progress of the compound in any given direction may be zero. This is the phenomenon that Lucretius illustrated with his image of a flock sheep on a distant hillside, which appears still even though the animals are individually in motion.

To conclude: Epicurean space is complementary to body, and exists where body is not. Bodies move through space, not as an immobile medium, but rather in the sense that space shifts its contours as bodies move. This characteristic of space is what Epicurus dubs its intangibility or failure to resist, as opposed to the tangibility of bodies: bodies are inalterable in shape, space is not. Space is infinitely extended, and although there is directionality in the universe (down versus up), this is not a property of space but rather of bodies, a function of the quality that Epicurus defined as weight. The relative quantity of space and bodies (taken as volumes) constitutes the density of compounds, and in this sense space may be said to contribute to the properties of objects. Space is empty – it is never filled or occupied – but it can be measured: it is three-dimensional, and the distance between bodies may be calculated in terms of the extent of space between them. Like any extended entity, there are greater and smaller stretches of it. Globally, its magnitude is infinite: there is no upper limit. But there is a lower limit to extension, which is the minimum known to thought that Epicurus stipulated as irreducible but not equal to zero, that is, not point sized. My own guess is that it is what Epicurus would call incomprehensibly small, in the sense that it requires an incomprehensibly large but not strictly infinite number of them to make up any finite length. Space thus has minimum parts in the same sense that bodies do, and the equal speed or ἰσοτάχεια at which atoms move is precisely one minimum of space per minimum of time. Sextus’ puzzle depends on this conception, and I see no reason to suppose that it was developed subsequent to the theory of the founder; but even if it was, it became part of the Epicurean conception of space, and I presume that Epicurus’ theory was not inhospitable to such an innovation.