PV Function

The PV function calculates the present value of an investment (or a loan), assuming a constant interest rate. This is the amount that a series of future payments is currently worth. You can use PV with regular payments (such as a mortgage or other loan), periodic payments, or the future value of a lump sum paid now.

Syntax

PV(rate, nper, pmt, [fv], [type])

Arguments

Please see the Definitions section above for more a detailed description of these arguments.

Arguments	Description
Rate	Required. This is the interest rate per period.
Nper	Required. The total number of payment periods in an annuity i.e. the term.
Pmt	Required. This is the payment made for each period in the annuity. If you omit pmt , you must include the fv argument.
Fv	Optional. This is the future value of an investment based on an assumed rate of growth. If you omit fv, it is assumed to be 0 (zero), for example, the future value of a loan is 0. If you omit fv then you must include the pmt argument.
Type	Optional. This argument is 0 or 1 and indicates when payments are due. 0 or omitted = at the end of the period. 1 = at the beginning of the period.

Some points to take into consideration when using annuity functions:

• You always need to express the rate argument in the same units as the nper argument. For example, say you have monthly payments on a three-year loan at 5% annual interest. If you use 5%/12 for rate , you must use 3*12 for nper . If the payments on the same loan are being made annually, then you would use 5% for rate and 3 for nper.
• In annuity functions, the cash paid out (like a payment to savings) is represented by a negative number. The cash you receive (like a dividend payment) is represented by a positive number. For example, a $500 deposit to the bank would be represented by the argument -500 if you are the depositor, and by the argument 500 if you are the bank.

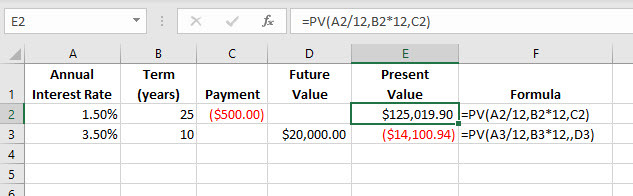
Example

In the example below, we use the PV formula to calculate:

1. The present value of a $500 monthly payment over 25 years at a rate of 1.5% interest.
2. The present value of the lump sum now needed to create $20,000 in 10 years at a rate of 3.5% interest.

Explanation of Formulas:

=PV(A2/12,B2*12,C2)

As you’ve probably noticed, the units for rate and nper have been kept consistent by specifying them in monthly terms, A2/12 and B2*12. The payment (pmt) has been entered in the worksheet as a negative value as this is money being paid out.

=PV(A3/12,B3*12,,D3)

The present value is a negative number as it shows the amount of cash that needs to be invested today (paid out) to generate the future value of $20,000 in 10 years at a rate of 3.5% interest.