FV Function
The FV function calculates the future value (at a specified date in the future) of an investment based on a constant interest rate. You can use FV to calculate the future value of regular payments, periodic payments, or a single lump sum payment.
Syntax
FV(rate,nper,pmt,[pv],[type])
Arguments
Please see the Definitions section of this chapter for more a detailed description of these arguments.
|
Arguments
|
Description
|
|
Rate
|
Required. This is the interest rate per period.
|
|
Nper
|
Required. The total number of payment periods in an annuity i.e. the term.
|
|
Pmt
|
Required. This is the payment made for each period in the annuity.
If you omit pmt, you must include pv.
|
|
Pv
|
Optional. This is the present value of an investment based on a constant growth rate.
If you omit pv, it is assumed to be 0 (zero) and you must include pmt.
|
|
Type
|
Optional. The type
is 0 or 1 and it indicates when payments are due.
0 (or omitted) = at the end of the period.
1 = at the beginning of the period.
|
Example
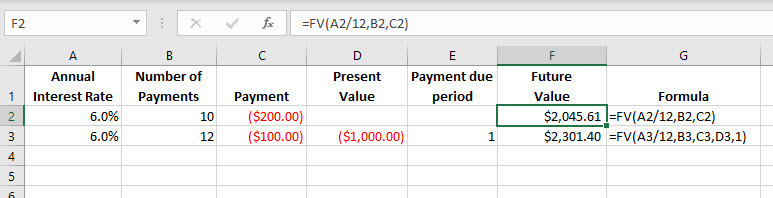
In the example below, we use the FV function to calculate:
- The future value of a monthly payment of $200 over 10 months at an interest of 6% per annum.
- The future value of a lump sum of $1,000 plus 12 monthly payments of $100, at an interest rate of 6%.
Explanation of Formulas:
=FV(A2/12,B2,C2)
Note that the rate
argument has been divided by 12 to represent monthly payments. The pmt
argument is a negative value (C2) as this is money being paid out.
=FV(A3/12,B3,C3,D3,1)
This formula has the pmt argument as well as the optional pv argument which represents the present value of the investment. The payment due period is 1 which means the payment starts at the beginning of the period.