NPV Function

The NPV function calculates the net present value which is the present value of cash inflows and cash outflows over a period. It calculates the present value of an investment by applying a discount rate and a series of future payments that may be income (positive values) or payments/losses (negative values).

Syntax

NPV(rate,value1,[value2],...)

Arguments

Argument	Description
Rate	Required. This is the percentage rate of discount over the length of the investment.
Value1	Required. This represents either a payment/loss (negative value) or income (positive value).
value2, ...	Optional: You can have additional values representing payments and income up to a total of 254 value arguments. The length of time between these payments must be equally spaced and occur at the end of each period.

Some points to note when using this function:

• The rate argument in the function might represent the rate of inflation or the interest rate that you might get from an alternative form of investment, for example, a high-yield savings account.
• The value arguments represent the projected income (or loss) values over the period of the investment.
• Ensure you enter the payment and income values in the correct order because NPV uses the order of the value arguments to interpret the order of cash flows.
• The NPV investment begins one period before the date of the first cash flow (value1) and ends with the last cash flow in the list of value arguments. If the first cash flow happens at the beginning of the period, you must add it to the result of the NPV function and not include it as one of its value arguments.
• The main difference between NPV and PV is that with PV, the cash flows can start at the beginning or end of the period while for NPV the cash flows start at the beginning of the period. Also, PV has the same cash flow amount throughout the investment while NPV can have different cash flow amounts.
• Arguments that are not numbers are ignored.

Example

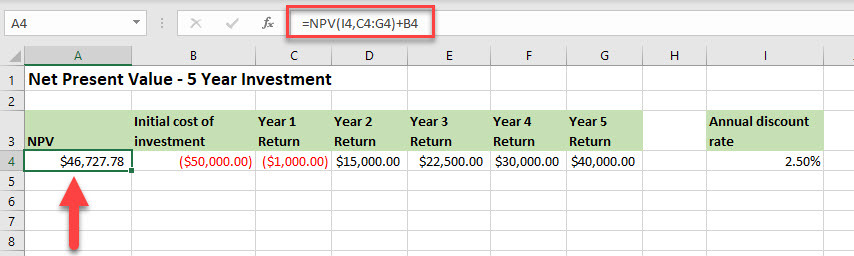
In the example below, we are calculating the net present value of an initial investment of $50,000 over the course of five years, considering an annual discount rate of 2.5 per cent.

Formula explanation

=NPV(I4,C4:G4)+B4

In the figure above, Year 1 of the investment shows a loss of $1,000, hence, this has been entered as a negative value. The other years of the investment (years two to five) returned a profit, so these were entered as positive values.

The function uses two arguments, the rate and value1 , which references cells C4:G4. The initial investment is added to the result returned by the function rather than being an argument in the function.

The result shows the net present value of the investment over five years is:

$46,727.78.