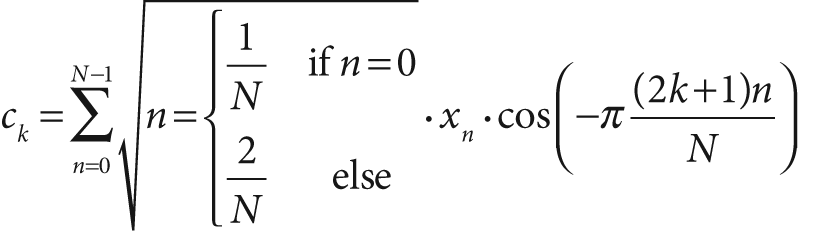Discrete Cosine Transform (DCT)

For real-valued data it is often sufficient to compute what is, in effect, only half of the discrete Fourier transform. The discrete cosine transform (DCT) [Ahmed74; Jain77] is defined analogously to the full DFT by the following formula:

Observe that, by convention, the normalization factor is applied to both the cosine transform and its inverse. Of course, there is a similar transform for higher dimensions.

The basic ideas of the DFT apply also to the DCT, but now all the coefficients are real-valued. Astute readers might object that the cosine transform is being applied to a vector that is not a manifestly even function. However, with cvDCT() the algorithm simply treats the vector as if it were extended to negative indices in a mirrored manner.

The actual OpenCV call is:

void cvDCT(
  const CvArr* src,
  CvArr*       dst,
  int          flags
);

The cvDCT() function expects arguments like those for cvDFT() except that, because the results are real-valued, there is no need for any special packing of the result array (or of the input array in the case of an inverse transform). The flags argument can be set to CV_DXT_FORWARD or CV_DXT_INVERSE, and either may be combined with CV_DXT_ROWS with the same effect as with cvDFT(). Because of the different normalization convention, both the forward and inverse cosine transforms always contain their respective contribution to the overall normalization of the transform; hence CV_DXT_SCALE plays no role in cvDCT.