CHAPTER 28
Basic statistics: sample size and power: How are sample size and power calculated?

Manish Garg¹, Richard Harrigan¹, and Gary Gaddis²

¹ Temple University Hospital and School of Medicine, Philadelphia, PA, USA

² St. Luke’s Hospital of Kansas City, MO, USA

Calculating an appropriate sample size to enable adequate statistical power is critical to planning any research study. A study that has an insufficient sample size and power will be unlikely to yield data that supports your hypothesis, even when that hypothesis is true. The consequence? Legions of readers will throw rotten tomatoes and lament “If only the study had been adequately powered to meet statistical significance!” Conversely, overly large sample sizes and power is not a good thing either. A study that is overly powered with astronomical sample sizes wastes resources because it could have been accomplished with fewer participants and less expense. Such studies are inherently able to deliver findings that may be statistically significant, but not clinically significant (e.g., think of cardiology registry studies where small changes in blood pressure show statistically but not clinically significant endpoints). So sample size and power is kind of like Goldilocks and the three bears – you want everything to be “just right.”

In order to calculate the optimum sample size and power for your study, you need to understand the following research concepts:

The purpose of sample size and power calculations.
Important definitions relevant to sample size and power calculations.
What is power?
Factors that will influence sample size and power.
When and how to calculate sample size and power.

The purpose of sample size and power calculations

Sample size and power calculations are estimates of how many participants are needed in a study [1]. Ideally, you would love to study a specific characteristic in the entire population, but this is rarely feasible. So instead, researchers measure the characteristic of interest in a select sample of the population and draw inferences about that population as a whole. Naturally, the greater the number of patients that are studied, the closer the measurements obtained in a study will approach the true value of those measurements in the entire population. We thus determine an estimation of sample size and power to figure out the minimum number of study participants needed to demonstrate a difference of a predetermined size or larger, without coming up short … and without expending the resources to study an excessive number of participants. (Remember Goldilocks; not too big, not too small, but just right.)

Important definitions relevant to sample size and power calculations

You are an enthusiastic researcher who is attempting to answer a scientific question. You would like your study to be able to demonstrate a statistically-significant difference between groups, if indeed a difference is present. You wish to design a study that is unlikely to reach an erroneous conclusion. So let us first define the two types of hypotheses you must understand:

The “null hypothesis” states that there is no difference between the two groups studied with respect to the variable(s) measured. The hypothesized size of difference between groups is exactly zero.
The “alternative hypothesis” states that there is a non-zero difference between the two groups studied with respect to the variable(s) measured – and it is inferred that the observed difference is due to effect(s) of the treatment.

The alternative hypothesis is actually an infinite number of hypotheses from a mathematical standpoint because the size of difference is hypothesized to be a non-zero value. Since the null hypothesis is a single hypothesis of zero difference, it is the null hypothesis that is tested mathematically. Inferential statistical testing is used to estimate the likelihood that the size of difference observed between groups occurred due to chance. By convention, differences that are less than 5% likely to have occurred due to chance are deemed to be significantly different from a statistical and probabilistic perspective. This is why the expression “p<0.05” is used to denote a statistically significant difference between groups.

If the mathematics of hypothesis testing suggests that the numerical difference between the two groups you studied is not statistically significant (which is to say the numerical difference is 5% or more likely to have occurred by chance alone), you accept the null hypothesis. If the size of the numerical difference between the groups you studied is large enough that it is statistically significant (which is to say that the numerical difference is less than 5% likely to have occurred by chance alone), you accept the alternative hypothesis. Ideally, you would like to establish an alternative hypothesis that is clinically meaningful (clinically significant), that will make you the envy of the scientific community, and catapult you to unprecedented fame and glory.

Whoa tiger, settle down! You need to make sure you have planned your study so that you are unlikely to have committed one of these errors:

A “Type I error” (a “false positive” represented by α) occurs when you incorrectly reject the null hypothesis (i.e., the null hypothesis is true, yet the inferential statistical tests applied to the study data led you to wrongly conclude that a statistically significant difference exists between study groups). By convention, researchers accept that most studies have a 5% chance of making this type of error. Type I errors can occur even though the researcher plans the study carefully and executes the study properly. One important means to decrease the probability of committing a Type I error is to minimize bias in a study’s methodology. (Chapter 10 provides more information about bias.)
A “Type II error” (a “false negative” represented by β) occurs when you incorrectly accept the null hypothesis (i.e., the alternative hypothesis is true, yet your inferential statistical test found no statistically different difference between study groups). By convention, via sample size planning, researchers accept a 10 or 20% probability of making these types of errors. So, Type II errors, like Type I errors, can occur even though the researcher plans the study carefully and executes the study properly. The most important means under a researcher’s control to decrease the probability of making a Type II error is to study a sufficient number of participants.

What is power?

Now that you understand the hypotheses and types of error, let us introduce the concept of power. Power is the probability that the study will reject the null hypothesis when the alternative hypothesis is true (i.e., the probability of not committing a Type II error). As power increases, the chance of committing a Type II error decreases. Since the probability of committing a Type II error is the false negative rate β, power is equal to 1 – β (which happens to be another formula for sensitivity; in other words, the sensitivity of the experiment to find a significant difference between study groups when the groups are in fact different).

Factors influencing sample size and power

So now that you have defined power, it is important to understand the following questions that will influence sample size and power in your study:

What statistical test do you want to use?
What is the measurement variance of the effect you are studying?
What is the magnitude (effect size) of the measured difference delta (δ) for which you are looking? (And is it clinically or just statistically significant?)
How important is the Type I or Type II error in determining your sample size?

Let us begin with the type of statistical test you want to use. It is important to note that the type of statistical test used affects how the sample size is calculated. Tests can be divided into parametric tests and non-parametric tests. Parametric tests deal with data that can be expected to be normally distributed and utilize the sample mean and the sample variance for their calculation. Non-parametric tests are used when the data are not normally distributed [like nominal (categorical) or ordinal (rank-ordered) data, a – see Chapter 27 for more information about this]. Parametric tests involve certain assumptions, such as that the data are normally distributed about the mean. If those assumptions are correct, parametric tests are more accurate and precise for determining differences between groups than non-parametric tests applied to the same data. (Parametric tests also have more power than non-parametric tests, but if the assumptions that underlie parametric tests are incorrect, those tests can deliver incorrect conclusions.) So, what does this mean for your study? Simple, you must determine if your data are likely to be normally distributed or not. If they are, you should choose a parametric test. If they are not, choose a non-parametric test, but realize that it will need more sample size than a parametric test to maintain power. The bottom line is that it is important to choose the right inferential test to analyze your data, and the characteristics of the inferential test will have an influence on the necessary sample size.

An example of parametric data is the height of male Americans. The data are measured on a continuously distributed scale, where the size of a difference of one unit is always the same (e.g., an inch is always an inch; a centimeter is always a centimeter). The height of male Americans will be “normally distributed”, which means that it will have a frequency distribution in the shape of a “bell curve.”

An example of ordinal data would be how those men respond to the statement, “I believe that the President is doing a good job.” The men could be offered a survey and they could use Likert Scale data (Strongly Agree, Agree, Neutral, Disagree, Strongly Disagree) to rate the job performance of the President. These data are unlikely to be normally distributed and the size of difference between data points is not constant or discoverable.

An example of categorical or nominal data would be the blood types of those men. How many are Type “A”, Type “B” Type “AB”, and Type “O”?

Another important factor influencing power and sample size is the measurement variance. Variance is mathematically related to the more commonly understood concept of standard deviation (which is the square root of variance). Variance measures how far a set of data points is spread out from the mean value. In your study, you are selecting a sample that will hopefully give you a probability distribution that accurately represents and includes the true value in the population. Now let’s suppose you use a 95% confidence interval to describe the reliability of your sample while hoping the true mean value is not located far from your sample mean value.

Since the size of a confidence interval is inversely proportional to the number of participants studied, you want to maximize your sample size to reduce the negative effects of variance. What is the take-home message? A study with a small sample size will have large confidence intervals and will show statistical significance only if there is a large difference between groups; the same study with a larger sample size will have smaller confidence intervals and so will be able to demonstrate a statistically significant difference, when the groups being compared actually differ, even with a small difference between groups. Another way to say this is that larger sample sizes yield more narrow confidence intervals for expressing the range of values in which the true population value, as inferred from sample data, is likely to lie. Further, larger sample sizes will be able to discern relatively small sizes of difference between groups as significantly different.

The next question to ask yourself is: “Is the magnitude of the measured difference between groups both statistically significant and clinically significant? The magnitude of the difference is termed “delta” (δ). This magnitude is also referred to as the “effect size.” Whereas you want a sample size that is sufficiently large to be powered to show a statistically significant difference, when a difference between groups is actually present, you also do not want to be overpowered, because you will waste time and resources. (You also potentially run the risk of finding a difference that is statistically but not clinically significant.) For example, registry studies (e.g., cardiology and trauma) at times involve thousands of patients that are typically retrospectively reviewed. Since the sample size and power in these studies are enormous, often very small findings (e.g., a few millimeters of mercury in a cardiology blood pressure registry study) can represent statistically significant differences between groups, which has minimal, if any, clinical significance. So if the mean blood pressure in a cardiology registry study is 150/80 in the treatment group, compared to a mean blood pressure of 154/84 in the placebo group, a numerical and statistical difference that is not clinically significant could result. Conversely, in an appropriately powered study with the right sample size, a blood pressure of 150/80 in the treatment group compared to a blood pressure of 165/100 in the placebo group that is (let us say) statistically significant would also represent a clinically significant distinction. What is the conclusion? An integral component of a sample size calculation is determining the size of difference between groups, δ, that you define as a clinically important difference. The sample size that is planned is the minimum sample size required, given the expected variances, to be 80 or 90% likely (depending on the power you choose) to find a difference between groups of size δ or larger (Box 28.1).

Box 28.1 A tale of statistically versus clinically significant results.

An example of a statistical difference that many eventually came to believe did not provide a clinically useful effect is the example of administering corticosteroids to patients with acute spinal cord injuries. The National Acute Spinal Cord Injury Studies (NASCIS) II [2] and III [3] provided evidence that patients with complete or incomplete spinal cord injuries could achieve statistically significant gains in sensory and motor function if high-dose corticosteroids were administered promptly; these studies changed the way care was provided for these patients. Later, Nesathurai and Shanker [4] performed a critique of these studies, citing various methodological issues that cast doubt on the conclusions and, more importantly, highlighted that the clinical gains from high-dose corticosteroids were questionable. In addition, high-dose corticosteroids have widely recognized adverse effects, such as an increased probability of infections and avascular necrosis of bone. This has resulted in a change of recommendations from professional societies regarding high-dose steroids. The Congress of Neurological Surgeons has concluded that high dose corticosteroid therapy “…should be undertaken with the knowledge that the evidence suggesting harmful side effects is more consistent than any suggestion of clinical benefit” [5]. The Canadian Association of Emergency Physicians also no longer recommends this therapy as the standard of care in spinal cord injured patients. The 2013 guidelines issued by the Congress of Neurological Surgeons and the American Association of Neurological Surgeons recommend against the use of high-dose steroids early after an acute spinal cord injury, due to the lack of medical evidence for their efficacy and the probability of harmful adverse effects [6].

And what about the influence of Type I and Type II errors? This is very important. Remember, Type I error occurs when we incorrectly reject the null hypothesis (i.e., the false positive rate) and a Type II error occurs when we incorrectly accept the null hypothesis (i.e., the false negative rate). When determining an acceptable probability threshold for Type I error (denoted pα), the industry standard is to choose a probability of <0.05. This means that, given a positive finding in a study, the chance of discovering this positive finding, or something greater, by chance, would occur on less than 5% of occasions. The pα of your study will be preset by you as you perform your sample size calculation (denoted, N). When determining an acceptable probability threshold for Type II error (denoted pβ), the industry standard is to choose a probability of 0.8–0.9. This means that if there is a true difference in a study, we will find it 80–90% of the time. So how do you bring it all together? Statistical power is (1 – pβ) and represents the probability that the study will detect a true difference of size δ between two study entities, given a preset value of pα and a sample size, N.

When should you perform a sample size calculation?

The answer to the above question is (100%) before you start your study, and often during or after the study concludes. Ideally, you would love to have the foresight and vision to establish a priori your sample size and power calculations such that you could accurately estimate the needed sample size 100% of the time. However, the reality of any study is that before collecting data, the researcher must make certain assumptions about the desired effect size and variance, and your original study assumptions may not be totally accurate. For this reason you may wish to perform interim power calculations, using the size of the variance actually observed (rather than the estimated size used when planning the study) to see if you have the Goldilocks amount of sample size to find a difference of size δ. If your study finds a significant difference between groups, by definition your study was not underpowered. However, when the statistics support the null hypothesis, it is possible that the study was underpowered. The researcher should calculate power, given the number of participants studied, the size of difference δ between groups that is deemed to be clinically significant, and the variance observed from the data. Remember, you do not want to come up short with your numbers and you do not want too many data points (especially if time, resources, or potentially adverse outcomes are declaring themselves). It is important to mention that you should be able to calculate the sample size and power when you are evaluating someone else’s work. That will let you know whether the large famous trial with “negative results” was likely to be due to the study being underpowered instead of a finding that should be trusted.

How do you perform a sample size and power calculation when testing for a possible difference between groups?

So let us put this all together with a concrete example and go through the mathematics. You probably will phone a statistician friend or order some specialized statistical software to perform your mathematical calculation for you (particularly if you are reporting categorical non-parametric data), but we can easily show an example of a comparative study that uses continuous normally distributed parametric data.

So, let us say you are trying to assist your emergency medicine colleagues from the scourge of rampant abscesses infesting the globe by studying a new antibiotic (RIFM) that is targeted against MRSA. From your previous pilot study and reviewing the literature, conventional antibiotics plus incision and drainage therapy takes, on average, four days to “heal” (which you will operationally define) with a standard deviation of three days. You believe RIFM (short for “Resistance is futile MRSA”) plus incision and drainage therapy should demonstrate an improved healing time of two days which you believe is clinically important. What kind of sample size would you need for this study using conventional error and power set points? [1]

Organizing our thoughts onto paper:

What is the null hypothesis?	That RIFM will demonstrate no improvement in time-to-healing over conventional therapy
What is the alternative hypothesis?	That RIFM will demonstrate an improvement in time-to-healing over conventional therapy
What type of data, what statistical test?	Continuous normally distributed, t-test
pα level to avoid a Type I error?	0.05
pβ level to avoid a Type II error?	0.8
What is the clinically important difference δ?	2 day improvement in healing
What is the standard deviation?	From other studies, we ascertained 3 days

Now we need to calculate the effect size, also known as the “standardized difference.” The equation for the standardized difference is:

So in our example the standardized difference = 2 days/3 days = 2/3 = 0.67. Next, to calculate our sample size we can either use a nomogram developed by Gore and Altman or a sample size formula. The Gore and Altman nomogram [7] is represented in Figure 28.1.

c28-fig-0001 — **Figure 28.1** The Gore and Altman Nomogram.

The Gore and Altman nomogram lists the standardized difference on the left vertical axis, the power on the right vertical axis, and the pα in the center (which will give you the sample size N which will need to be divided into two treatment groups). You make a line from the standardized difference to the power and “Eureka,” you have your sample size. Let us plug in our numbers. Since the standardized difference is 0.67 and the power is 0.8, our line would intersect the sample size line at 70 participants – requiring 35 patients in the RIFM group and 35 patients in the conventional therapy group (plotted in Figure 28.2).

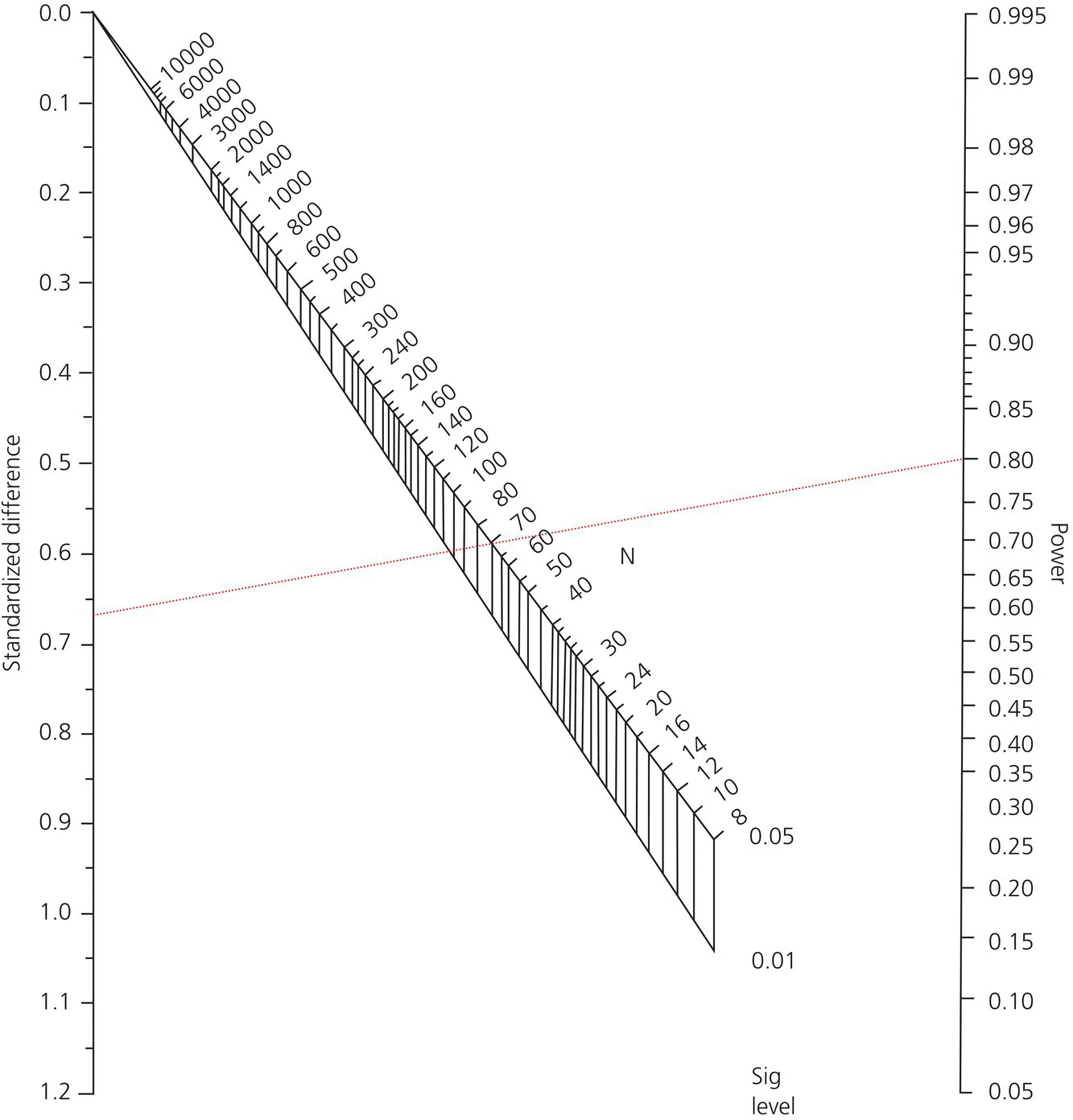
c28-fig-0002 — **Figure 28.2** Sample size example.

The other method of determining sample size is to use a sample size formula. The sample size formula [8] is:

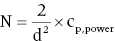
where “N” represents the number of participants required in each group, “d” represents the standardized difference, and c_p,power represents a constant defined by the values chosen for the pα value and pβ (power). Commonly used values for c_p,power are shown in Table 28.1.

Table 28.1 Common values for c_p,power.

pα	pβ
	0.50	0.80	0.90	0.95
0.05	3.8	7.9	10.5	13.0
0.01	6.6	11.7	14.9	17.8

Entering our values in the formula: N = 2/(0.67)² × 7.9 (from pα of 0.05 and pβ of 0.80) = 35. Remember N = the number of participants required in each group, so you will need 35 patients in the RIFM group and 35 patients in the conventional therapy group. This is the same result as that obtained with the nomogram. You should practice adjusting the pα and pβ to understand the effect on your sample size.

How do you perform a sample size and power calculation when undertaking an equivalence or non-inferiority trial?

Our trial above, and really, the discussion for the entire chapter, has been about trying to prove that one drug is better than another. A non-inferiority trial is undertaken when a proposed new therapy represents less burden on the patient than the standard therapy. For example, consider a choice between two drugs to treat ventilator-acquired pneumonia. Clearly, if you wish to treat pneumonia, you want the drug that you pick to cure the patient, and you do not want the drug to cause adverse effects. Let us say that two drugs are options to use “Gentle-cillin,” which recent data suggest seems effective, and “Gorilla-cillin,” which has long been the current standard of care. If “Gorilla-cillin” has a high side effect profile, such as a high likelihood to cause Clostridium difficile colitis, and “Gentle-cillin” has less likelihood of causing this side effect, the question you should be asking is, “Is Gentle-cillin about as likely to cure the patient as Gorilla-cillin?” This is because you want to give the patient the best drug, the drug that is likely to enable a cure without causing adverse effects. The question of defining exactly what is meant by “about as likely to cure” involves subjective choices about what numerical difference of pneumonia cure rate is small enough to judge the differences between the two drugs to be negligible. The assumptions that go into calculating the necessary sample size for such an equivalence or even non-inferiority trial (in which you are asking if one drug is “not worse” than another) are more complex than is the case for trials that look for a difference between treatments. If the reader wishes to learn more about sample size calculation for equivalence or non-inferiority trials, they are encouraged to consult a more comprehensive statistical text.

Summary

In summary, understanding and calculating sample size and power is critical to your study. You now have been given the power to determine one of the most important characteristics of your study – the sample size. What are you waiting for?

KEY POINTS

Sample size and power calculations are estimates of how many participants are needed in a study.
The “null hypothesis” states that there is no difference between the two groups studied with respect to the variable(s) measured.
The “alternative hypothesis” states that there is a non-zero difference between the two groups studied with respect to the variable(s) measured.
A “Type I Error” (a “false positive”) occurs when you incorrectly reject the null hypothesis.
A “Type II Error” (a “false negative”) occurs when you incorrectly accept the null hypothesis.
Power is the probability that the study will reject the null hypothesis when the alternative hypothesis is true.
Variance measures how far a set of data points is spread out from the mean value.
The best studies are both statistically and clinically significant.

References

1 Jones, S.R., Carley, S., and Harrison, M. (2003) An introduction to power and sample size estimation. Emerg Med J, 20:453–458.
2 Bracken, M.B., Shepard, M.J., Hellenbrand, K.G., et al. (1985) Methylprednisolone and neurological function 1 year after spinal cord injury. Results of the National Acute Spinal Cord Injury Study. J Neurosurg, 63(5):704–713.
3 Bracken, M.B., Shepard, M.J., Holford, T.R., et al. (1997) Administration of methylprednisolone for 24 or 48 hours or tirilazad mesylate for 48 hours in the treatment of acute spinal cord injury. Results of the Third National Acute Spinal Cord Injury Randomized Controlled Trial. National Acute Spinal Cord Injury Study. JAMA, 277(20):1597–1604.
4 Nesathurai, S. (1998) Steroids and spinal cord injury: revisiting the NASCIS 2 and NASCIS 3 trials. J Trauma, 45(6):1088–1093.
5 Hadley, M.N., Walters, B.C., Grabb, P.A., et al. (2002) Pharmacological therapy after acute spinal cord injury. Neurosurgery, 50(Suppl):63–72.
6 Hadley, M.N. and Walters, B.C. (2013) Guidelines for the management of acute cervical spine and spinal cord injuries. Neurosurgery, 72(Suppl 2):1–259.
7 Gore, S.M. and Altman, D.G. (2001) How Large a Sample. Statistics in Practice. BMJ Publishing, London, pp. 6–8.
8 Whitley, E. and Ball, J. (2002) Statistics review 4: Sample size calculations. Crit Care, 6(4):335–341.