Fig. 1.PROP. I. Theor. I.
The Phænomena of Colours in refracted or reflected Light are not caused by new Modifications of the Light variously impress’d, according to the various Terminations of the Light and Shadow.
The Proof by Experiments.
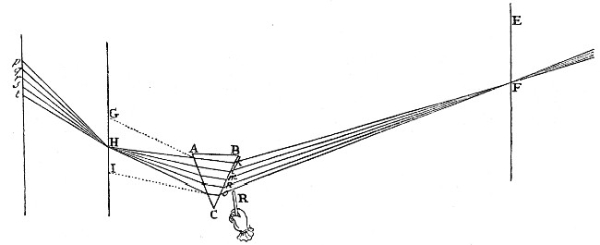
Exper. 1. For if the Sun shine into a very dark Chamber through an oblong hole F, [in Fig. 1.] whose breadth is the sixth or eighth part of an Inch, or something less; and his beam FH do afterwards pass first through a very large Prism ABC, distant about 20 Feet from the hole, and parallel to it, and then (with its white part) through an oblong hole H, whose breadth is about the fortieth or sixtieth part of an Inch, and which is made in a black opake Body GI, and placed at the distance of two or three Feet from the Prism, in a parallel Situation both to the Prism and to the former hole, and if this white Light thus transmitted through the hole H, fall afterwards upon a white Paper pt, placed after that hole H, at the distance of three or four Feet from it, and there paint the usual Colours of the Prism, suppose red at t, yellow at s, green at r, blue at q, and violet at p; you may with an Iron Wire, or any such like slender opake Body, whose breadth is about the tenth part of an Inch, by intercepting the Rays at k, l, m, n or o, take away any one of the Colours at t, s, r, q or p, whilst the other Colours remain upon the Paper as before; or with an Obstacle something bigger you may take away any two, or three, or four Colours together, the rest remaining: So that any one of the Colours as well as violet may become outmost in the Confine of the Shadow towards p, and any one of them as well as red may become outmost in the Confine of the Shadow towards t, and any one of them may also border upon the Shadow made within the Colours by the Obstacle R intercepting some intermediate part of the Light; and, lastly, any one of them by being left alone, may border upon the Shadow on either hand. All the Colours have themselves indifferently to any Confines of Shadow, and therefore the differences of these Colours from one another, do not arise from the different Confines of Shadow, whereby Light is variously modified, as has hitherto been the Opinion of Philosophers. In trying these things ’tis to be observed, that by how much the holes F and H are narrower, and the Intervals between them and the Prism greater, and the Chamber darker, by so much the better doth the Experiment succeed; provided the Light be not so far diminished, but that the Colours at pt be sufficiently visible. To procure a Prism of solid Glass large enough for this Experiment will be difficult, and therefore a prismatick Vessel must be made of polish’d Glass Plates cemented together, and filled with salt Water or clear Oil.
Fig. 1.
Exper. 2. The Sun’s Light let into a dark Chamber through the round hole F, [in Fig. 2.] half an Inch wide, passed first through the Prism ABC placed at the hole, and then through a Lens PT something more than four Inches broad, and about eight Feet distant from the Prism, and thence converged to O the Focus of the Lens distant from it about three Feet, and there fell upon a white Paper DE. If that Paper was perpendicular to that Light incident upon it, as ’tis represented in the posture DE, all the Colours upon it at O appeared white. But if the Paper being turned about an Axis parallel to the Prism, became very much inclined to the Light, as ’tis represented in the Positions de and δε; the same Light in the one case appeared yellow and red, in the other blue. Here one and the same part of the Light in one and the same place, according to the various Inclinations of the Paper, appeared in one case white, in another yellow or red, in a third blue, whilst the Confine of Light and shadow, and the Refractions of the Prism in all these cases remained the same.
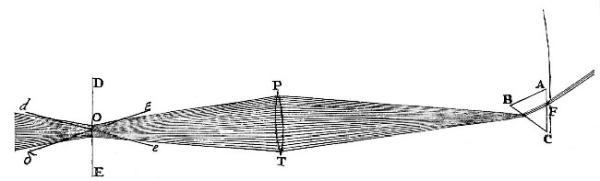Fig. 2.
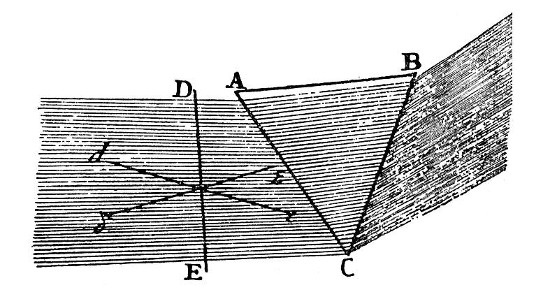Fig. 3.
Exper. 3. Such another Experiment may be more easily tried as follows. Let a broad beam of the Sun’s Light coming into a dark Chamber through a hole in the Window-shut be refracted by a large Prism ABC, [in Fig. 3.] whose refracting Angle C is more than 60 Degrees, and so soon as it comes out of the Prism, let it fall upon the white Paper DE glewed upon a stiff Plane; and this Light, when the Paper is perpendicular to it, as ’tis represented in DE, will appear perfectly white upon the Paper; but when the Paper is very much inclin’d to it in such a manner as to keep always parallel to the Axis of the Prism, the whiteness of the whole Light upon the Paper will according to the inclination of the Paper this way or that way, change either into yellow and red, as in the posture de, or into blue and violet, as in the posture δε. And if the Light before it fall upon the Paper be twice refracted the same way by two parallel Prisms, these Colours will become the more conspicuous. Here all the middle parts of the broad beam of white Light which fell upon the Paper, did without any Confine of Shadow to modify it, become colour’d all over with one uniform Colour, the Colour being always the same in the middle of the Paper as at the edges, and this Colour changed according to the various Obliquity of the reflecting Paper, without any change in the Refractions or Shadow, or in the Light which fell upon the Paper. And therefore these Colours are to be derived from some other Cause than the new Modifications of Light by Refractions and Shadows.
If it be asked, what then is their Cause? I answer, That the Paper in the posture de, being more oblique to the more refrangible Rays than to the less refrangible ones, is more strongly illuminated by the latter than by the former, and therefore the less refrangible Rays are predominant in the reflected Light. And where-ever they are predominant in any Light, they tinge it with red or yellow, as may in some measure appear by the first Proposition of the first Part of this Book, and will more fully appear hereafter. And the contrary happens in the posture of the Paper δε, the more refrangible Rays being then predominant which always tinge Light with blues and violets.
Exper. 4. The Colours of Bubbles with which Children play are various, and change their Situation variously, without any respect to any Confine or Shadow. If such a Bubble be cover’d with a concave Glass, to keep it from being agitated by any Wind or Motion of the Air, the Colours will slowly and regularly change their situation, even whilst the Eye and the Bubble, and all Bodies which emit any Light, or cast any Shadow, remain unmoved. And therefore their Colours arise from some regular Cause which depends not on any Confine of Shadow. What this Cause is will be shewed in the next Book.
To these Experiments may be added the tenth Experiment of the first Part of this first Book, where the Sun’s Light in a dark Room being trajected through the parallel Superficies of two Prisms tied together in the form of a Parallelopipede, became totally of one uniform yellow or red Colour, at its emerging out of the Prisms. Here, in the production of these Colours, the Confine of Shadow can have nothing to do. For the Light changes from white to yellow, orange and red successively, without any alteration of the Confine of Shadow: And at both edges of the emerging Light where the contrary Confines of Shadow ought to produce different Effects, the Colour is one and the same, whether it be white, yellow, orange or red: And in the middle of the emerging Light, where there is no Confine of Shadow at all, the Colour is the very same as at the edges, the whole Light at its very first Emergence being of one uniform Colour, whether white, yellow, orange or red, and going on thence perpetually without any change of Colour, such as the Confine of Shadow is vulgarly supposed to work in refracted Light after its Emergence. Neither can these Colours arise from any new Modifications of the Light by Refractions, because they change successively from white to yellow, orange and red, while the Refractions remain the same, and also because the Refractions are made contrary ways by parallel Superficies which destroy one another’s Effects. They arise not therefore from any Modifications of Light made by Refractions and Shadows, but have some other Cause. What that Cause is we shewed above in this tenth Experiment, and need not here repeat it.
There is yet another material Circumstance of this Experiment. For this emerging Light being by a third Prism HIK [in Fig. 22. Part I.][I] refracted towards the Paper PT, and there painting the usual Colours of the Prism, red, yellow, green, blue, violet: If these Colours arose from the Refractions of that Prism modifying the Light, they would not be in the Light before its Incidence on that Prism. And yet in that Experiment we found, that when by turning the two first Prisms about their common Axis all the Colours were made to vanish but the red; the Light which makes that red being left alone, appeared of the very same red Colour before its Incidence on the third Prism. And in general we find by other Experiments, that when the Rays which differ in Refrangibility are separated from one another, and any one Sort of them is considered apart, the Colour of the Light which they compose cannot be changed by any Refraction or Reflexion whatever, as it ought to be were Colours nothing else than Modifications of Light caused by Refractions, and Reflexions, and Shadows. This Unchangeableness of Colour I am now to describe in the following Proposition.
PROP. II. Theor. II.
All homogeneal Light has its proper Colour answering to its Degree of Refrangibility, and that Colour cannot be changed by Reflexions and Refractions.
In the Experiments of the fourth Proposition of the first Part of this first Book, when I had separated the heterogeneous Rays from one another, the Spectrum pt formed by the separated Rays, did in the Progress from its End p, on which the most refrangible Rays fell, unto its other End t, on which the least refrangible Rays fell, appear tinged with this Series of Colours, violet, indigo, blue, green, yellow, orange, red, together with all their intermediate Degrees in a continual Succession perpetually varying. So that there appeared as many Degrees of Colours, as there were sorts of Rays differing in Refrangibility.
Exper. 5. Now, that these Colours could not be changed by Refraction, I knew by refracting with a Prism sometimes one very little Part of this Light, sometimes another very little Part, as is described in the twelfth Experiment of the first Part of this Book. For by this Refraction the Colour of the Light was never changed in the least. If any Part of the red Light was refracted, it remained totally of the same red Colour as before. No orange, no yellow, no green or blue, no other new Colour was produced by that Refraction. Neither did the Colour any ways change by repeated Refractions, but continued always the same red entirely as at first. The like Constancy and Immutability I found also in the blue, green, and other Colours. So also, if I looked through a Prism upon any Body illuminated with any part of this homogeneal Light, as in the fourteenth Experiment of the first Part of this Book is described; I could not perceive any new Colour generated this way. All Bodies illuminated with compound Light appear through Prisms confused, (as was said above) and tinged with various new Colours, but those illuminated with homogeneal Light appeared through Prisms neither less distinct, nor otherwise colour’d, than when viewed with the naked Eyes. Their Colours were not in the least changed by the Refraction of the interposed Prism. I speak here of a sensible Change of Colour: For the Light which I here call homogeneal, being not absolutely homogeneal, there ought to arise some little Change of Colour from its Heterogeneity. But, if that Heterogeneity was so little as it might be made by the said Experiments of the fourth Proposition, that Change was not sensible, and therefore in Experiments, where Sense is Judge, ought to be accounted none at all.
Exper. 6. And as these Colours were not changeable by Refractions, so neither were they by Reflexions. For all white, grey, red, yellow, green, blue, violet Bodies, as Paper, Ashes, red Lead, Orpiment, Indico Bise, Gold, Silver, Copper, Grass, blue Flowers, Violets, Bubbles of Water tinged with various Colours, Peacock’s Feathers, the Tincture of Lignum Nephriticum, and such-like, in red homogeneal Light appeared totally red, in blue Light totally blue, in green Light totally green, and so of other Colours. In the homogeneal Light of any Colour they all appeared totally of that same Colour, with this only Difference, that some of them reflected that Light more strongly, others more faintly. I never yet found any Body, which by reflecting homogeneal Light could sensibly change its Colour.
From all which it is manifest, that if the Sun’s Light consisted of but one sort of Rays, there would be but one Colour in the whole World, nor would it be possible to produce any new Colour by Reflexions and Refractions, and by consequence that the variety of Colours depends upon the Composition of Light.
DEFINITION.
The homogeneal Light and Rays which appear red, or rather make Objects appear so, I call Rubrifick or Red-making; those which make Objects appear yellow, green, blue, and violet, I call Yellow-making, Green-making, Blue-making, Violet-making, and so of the rest. And if at any time I speak of Light and Rays as coloured or endued with Colours, I would be understood to speak not philosophically and properly, but grossly, and accordingly to such Conceptions as vulgar People in seeing all these Experiments would be apt to frame. For the Rays to speak properly are not coloured. In them there is nothing else than a certain Power and Disposition to stir up a Sensation of this or that Colour. For as Sound in a Bell or musical String, or other sounding Body, is nothing but a trembling Motion, and in the Air nothing but that Motion propagated from the Object, and in the Sensorium ’tis a Sense of that Motion under the Form of Sound; so Colours in the Object are nothing but a Disposition to reflect this or that sort of Rays more copiously than the rest; in the Rays they are nothing but their Dispositions to propagate this or that Motion into the Sensorium, and in the Sensorium they are Sensations of those Motions under the Forms of Colours.
PROP. III. Prob. I.
To define the Refrangibility of the several sorts of homogeneal Light answering to the several Colours.
For determining this Problem I made the following Experiment.[J]
Exper. 7. When I had caused the Rectilinear Sides AF, GM, [in Fig. 4.] of the Spectrum of Colours made by the Prism to be distinctly defined, as in the fifth Experiment of the first Part of this Book is described, there were found in it all the homogeneal Colours in the same Order and Situation one among another as in the Spectrum of simple Light, described in the fourth Proposition of that Part. For the Circles of which the Spectrum of compound Light PT is composed, and which in the middle Parts of the Spectrum interfere, and are intermix’d with one another, are not intermix’d in their outmost Parts where they touch those Rectilinear Sides AF and GM. And therefore, in those Rectilinear Sides when distinctly defined, there is no new Colour generated by Refraction. I observed also, that if any where between the two outmost Circles TMF and PGA a Right Line, as γδ, was cross to the Spectrum, so as both Ends to fall perpendicularly upon its Rectilinear Sides, there appeared one and the same Colour, and degree of Colour from one End of this Line to the other. I delineated therefore in a Paper the Perimeter of the Spectrum FAP GMT, and in trying the third Experiment of the first Part of this Book, I held the Paper so that the Spectrum might fall upon this delineated Figure, and agree with it exactly, whilst an Assistant, whose Eyes for distinguishing Colours were more critical than mine, did by Right Lines αβ, γδ, εζ, &c. drawn cross the Spectrum, note the Confines of the Colours, that is of the red MαβF, of the orange αγδβ, of the yellow γεζδ, of the green ηθζ, of the blue ηικθ, of the indico ιλμκ, and of the violet λGAμ. And this Operation being divers times repeated both in the same, and in several Papers, I found that the Observations agreed well enough with one another, and that the Rectilinear Sides MG and FA were by the said cross Lines divided after the manner of a Musical Chord. Let GM be produced to X, that MX may be equal to GM, and conceive GX, λX, ιX, ηX, εX, γX, αX, MX, to be in proportion to one another, as the Numbers, 1, 8/9, 5/6, 3/4, 2/3, 3/5, 9/16, 1/2, and so to represent the Chords of the Key, and of a Tone, a third Minor, a fourth, a fifth, a sixth Major, a seventh and an eighth above that Key: And the Intervals Mα, αγ, γε, εη, ηι, ιλ, and λG, will be the Spaces which the several Colours (red, orange, yellow, green, blue, indigo, violet) take up.
Fig. 4.
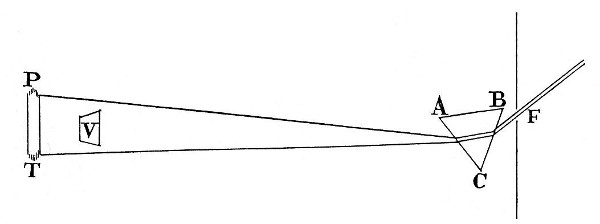Fig. 5.
Now these Intervals or Spaces subtending the Differences of the Refractions of the Rays going to the Limits of those Colours, that is, to the Points M, α, γ, ε, η, ι, λ, G, may without any sensible Error be accounted proportional to the Differences of the Sines of Refraction of those Rays having one common Sine of Incidence, and therefore since the common Sine of Incidence of the most and least refrangible Rays out of Glass into Air was (by a Method described above) found in proportion to their Sines of Refraction, as 50 to 77 and 78, divide the Difference between the Sines of Refraction 77 and 78, as the Line GM is divided by those Intervals, and you will have 77, 77-1/8, 77-1/5, 77-1/3, 77-1/2, 77-2/3, 77-7/9, 78, the Sines of Refraction of those Rays out of Glass into Air, their common Sine of Incidence being 50. So then the Sines of the Incidences of all the red-making Rays out of Glass into Air, were to the Sines of their Refractions, not greater than 50 to 77, nor less than 50 to 77-1/8, but they varied from one another according to all intermediate Proportions. And the Sines of the Incidences of the green-making Rays were to the Sines of their Refractions in all Proportions from that of 50 to 77-1/3, unto that of 50 to 77-1/2. And by the like Limits above-mentioned were the Refractions of the Rays belonging to the rest of the Colours defined, the Sines of the red-making Rays extending from 77 to 77-1/8, those of the orange-making from 77-1/8 to 77-1/5, those of the yellow-making from 77-1/5 to 77-1/3, those of the green-making from 77-1/3 to 77-1/2, those of the blue-making from 77-1/2 to 77-2/3, those of the indigo-making from 77-2/3 to 77-7/9, and those of the violet from 77-7/9, to 78.
These are the Laws of the Refractions made out of Glass into Air, and thence by the third Axiom of the first Part of this Book, the Laws of the Refractions made out of Air into Glass are easily derived.
Exper. 8. I found moreover, that when Light goes out of Air through several contiguous refracting Mediums as through Water and Glass, and thence goes out again into Air, whether the refracting Superficies be parallel or inclin’d to one another, that Light as often as by contrary Refractions ’tis so corrected, that it emergeth in Lines parallel to those in which it was incident, continues ever after to be white. But if the emergent Rays be inclined to the incident, the Whiteness of the emerging Light will by degrees in passing on from the Place of Emergence, become tinged in its Edges with Colours. This I try’d by refracting Light with Prisms of Glass placed within a Prismatick Vessel of Water. Now those Colours argue a diverging and separation of the heterogeneous Rays from one another by means of their unequal Refractions, as in what follows will more fully appear. And, on the contrary, the permanent whiteness argues, that in like Incidences of the Rays there is no such separation of the emerging Rays, and by consequence no inequality of their whole Refractions. Whence I seem to gather the two following Theorems.
1. The Excesses of the Sines of Refraction of several sorts of Rays above their common Sine of Incidence when the Refractions are made out of divers denser Mediums immediately into one and the same rarer Medium, suppose of Air, are to one another in a given Proportion.
2. The Proportion of the Sine of Incidence to the Sine of Refraction of one and the same sort of Rays out of one Medium into another, is composed of the Proportion of the Sine of Incidence to the Sine of Refraction out of the first Medium into any third Medium, and of the Proportion of the Sine of Incidence to the Sine of Refraction out of that third Medium into the second Medium.
By the first Theorem the Refractions of the Rays of every sort made out of any Medium into Air are known by having the Refraction of the Rays of any one sort. As for instance, if the Refractions of the Rays of every sort out of Rain-water into Air be desired, let the common Sine of Incidence out of Glass into Air be subducted from the Sines of Refraction, and the Excesses will be 27, 27-1/8, 27-1/5, 27-1/3, 27-1/2, 27-2/3, 27-7/9, 28. Suppose now that the Sine of Incidence of the least refrangible Rays be to their Sine of Refraction out of Rain-water into Air as 3 to 4, and say as 1 the difference of those Sines is to 3 the Sine of Incidence, so is 27 the least of the Excesses above-mentioned to a fourth Number 81; and 81 will be the common Sine of Incidence out of Rain-water into Air, to which Sine if you add all the above-mentioned Excesses, you will have the desired Sines of the Refractions 108, 108-1/8, 108-1/5, 108-1/3, 108-1/2, 108-2/3, 108-7/9, 109.
By the latter Theorem the Refraction out of one Medium into another is gathered as often as you have the Refractions out of them both into any third Medium. As if the Sine of Incidence of any Ray out of Glass into Air be to its Sine of Refraction, as 20 to 31, and the Sine of Incidence of the same Ray out of Air into Water, be to its Sine of Refraction as 4 to 3; the Sine of Incidence of that Ray out of Glass into Water will be to its Sine of Refraction as 20 to 31 and 4 to 3 jointly, that is, as the Factum of 20 and 4 to the Factum of 31 and 3, or as 80 to 93.
And these Theorems being admitted into Opticks, there would be scope enough of handling that Science voluminously after a new manner,[K] not only by teaching those things which tend to the perfection of Vision, but also by determining mathematically all kinds of Phænomena of Colours which could be produced by Refractions. For to do this, there is nothing else requisite than to find out the Separations of heterogeneous Rays, and their various Mixtures and Proportions in every Mixture. By this way of arguing I invented almost all the Phænomena described in these Books, beside some others less necessary to the Argument; and by the successes I met with in the Trials, I dare promise, that to him who shall argue truly, and then try all things with good Glasses and sufficient Circumspection, the expected Event will not be wanting. But he is first to know what Colours will arise from any others mix’d in any assigned Proportion.
PROP. IV. Theor. III.
Colours may be produced by Composition which shall be like to the Colours of homogeneal Light as to the Appearance of Colour, but not as to the Immutability of Colour and Constitution of Light. And those Colours by how much they are more compounded by so much are they less full and intense, and by too much Composition they maybe diluted and weaken’d till they cease, and the Mixture becomes white or grey. There may be also Colours produced by Composition, which are not fully like any of the Colours of homogeneal Light.
For a Mixture of homogeneal red and yellow compounds an Orange, like in appearance of Colour to that orange which in the series of unmixed prismatick Colours lies between them; but the Light of one orange is homogeneal as to Refrangibility, and that of the other is heterogeneal, and the Colour of the one, if viewed through a Prism, remains unchanged, that of the other is changed and resolved into its component Colours red and yellow. And after the same manner other neighbouring homogeneal Colours may compound new Colours, like the intermediate homogeneal ones, as yellow and green, the Colour between them both, and afterwards, if blue be added, there will be made a green the middle Colour of the three which enter the Composition. For the yellow and blue on either hand, if they are equal in quantity they draw the intermediate green equally towards themselves in Composition, and so keep it as it were in Æquilibrion, that it verge not more to the yellow on the one hand, and to the blue on the other, but by their mix’d Actions remain still a middle Colour. To this mix’d green there may be farther added some red and violet, and yet the green will not presently cease, but only grow less full and vivid, and by increasing the red and violet, it will grow more and more dilute, until by the prevalence of the added Colours it be overcome and turned into whiteness, or some other Colour. So if to the Colour of any homogeneal Light, the Sun’s white Light composed of all sorts of Rays be added, that Colour will not vanish or change its Species, but be diluted, and by adding more and more white it will be diluted more and more perpetually. Lastly, If red and violet be mingled, there will be generated according to their various Proportions various Purples, such as are not like in appearance to the Colour of any homogeneal Light, and of these Purples mix’d with yellow and blue may be made other new Colours.
PROP. V. Theor. IV.
Whiteness and all grey Colours between white and black, may be compounded of Colours, and the whiteness of the Sun’s Light is compounded of all the primary Colours mix’d in a due Proportion.
The Proof by Experiments.
Exper. 9. The Sun shining into a dark Chamber through a little round hole in the Window-shut, and his Light being there refracted by a Prism to cast his coloured Image PT [in Fig. 5.] upon the opposite Wall: I held a white Paper V to that image in such manner that it might be illuminated by the colour’d Light reflected from thence, and yet not intercept any part of that Light in its passage from the Prism to the Spectrum. And I found that when the Paper was held nearer to any Colour than to the rest, it appeared of that Colour to which it approached nearest; but when it was equally or almost equally distant from all the Colours, so that it might be equally illuminated by them all it appeared white. And in this last situation of the Paper, if some Colours were intercepted, the Paper lost its white Colour, and appeared of the Colour of the rest of the Light which was not intercepted. So then the Paper was illuminated with Lights of various Colours, namely, red, yellow, green, blue and violet, and every part of the Light retained its proper Colour, until it was incident on the Paper, and became reflected thence to the Eye; so that if it had been either alone (the rest of the Light being intercepted) or if it had abounded most, and been predominant in the Light reflected from the Paper, it would have tinged the Paper with its own Colour; and yet being mixed with the rest of the Colours in a due proportion, it made the Paper look white, and therefore by a Composition with the rest produced that Colour. The several parts of the coloured Light reflected from the Spectrum, whilst they are propagated from thence through the Air, do perpetually retain their proper Colours, because wherever they fall upon the Eyes of any Spectator, they make the several parts of the Spectrum to appear under their proper Colours. They retain therefore their proper Colours when they fall upon the Paper V, and so by the confusion and perfect mixture of those Colours compound the whiteness of the Light reflected from thence.
Exper. 10. Let that Spectrum or solar Image PT [in Fig. 6.] fall now upon the Lens MN above four Inches broad, and about six Feet distant from the Prism ABC and so figured that it may cause the coloured Light which divergeth from the Prism to converge and meet again at its Focus G, about six or eight Feet distant from the Lens, and there to fall perpendicularly upon a white Paper DE. And if you move this Paper to and fro, you will perceive that near the Lens, as at de, the whole solar Image (suppose at pt) will appear upon it intensely coloured after the manner above-explained, and that by receding from the Lens those Colours will perpetually come towards one another, and by mixing more and more dilute one another continually, until at length the Paper come to the Focus G, where by a perfect mixture they will wholly vanish and be converted into whiteness, the whole Light appearing now upon the Paper like a little white Circle. And afterwards by receding farther from the Lens, the Rays which before converged will now cross one another in the Focus G, and diverge from thence, and thereby make the Colours to appear again, but yet in a contrary order; suppose at δε, where the red t is now above which before was below, and the violet p is below which before was above.
Let us now stop the Paper at the Focus G, where the Light appears totally white and circular, and let us consider its whiteness. I say, that this is composed of the converging Colours. For if any of those Colours be intercepted at the Lens, the whiteness will cease and degenerate into that Colour which ariseth from the composition of the other Colours which are not intercepted. And then if the intercepted Colours be let pass and fall upon that compound Colour, they mix with it, and by their mixture restore the whiteness. So if the violet, blue and green be intercepted, the remaining yellow, orange and red will compound upon the Paper an orange, and then if the intercepted Colours be let pass, they will fall upon this compounded orange, and together with it decompound a white. So also if the red and violet be intercepted, the remaining yellow, green and blue, will compound a green upon the Paper, and then the red and violet being let pass will fall upon this green, and together with it decompound a white. And that in this Composition of white the several Rays do not suffer any Change in their colorific Qualities by acting upon one another, but are only mixed, and by a mixture of their Colours produce white, may farther appear by these Arguments.
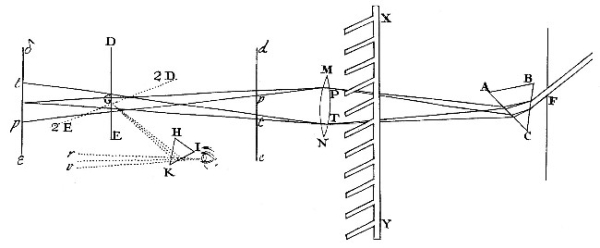Fig. 6.
If the Paper be placed beyond the Focus G, suppose at δε, and then the red Colour at the Lens be alternately intercepted, and let pass again, the violet Colour on the Paper will not suffer any Change thereby, as it ought to do if the several sorts of Rays acted upon one another in the Focus G, where they cross. Neither will the red upon the Paper be changed by any alternate stopping, and letting pass the violet which crosseth it.
And if the Paper be placed at the Focus G, and the white round Image at G be viewed through the Prism HIK, and by the Refraction of that Prism be translated to the place rv, and there appear tinged with various Colours, namely, the violet at v and red at r, and others between, and then the red Colours at the Lens be often stopp’d and let pass by turns, the red at r will accordingly disappear, and return as often, but the violet at v will not thereby suffer any Change. And so by stopping and letting pass alternately the blue at the Lens, the blue at v will accordingly disappear and return, without any Change made in the red at r. The red therefore depends on one sort of Rays, and the blue on another sort, which in the Focus G where they are commix’d, do not act on one another. And there is the same Reason of the other Colours.
I considered farther, that when the most refrangible Rays Pp, and the least refrangible ones Tt, are by converging inclined to one another, the Paper, if held very oblique to those Rays in the Focus G, might reflect one sort of them more copiously than the other sort, and by that Means the reflected Light would be tinged in that Focus with the Colour of the predominant Rays, provided those Rays severally retained their Colours, or colorific Qualities in the Composition of White made by them in that Focus. But if they did not retain them in that White, but became all of them severally endued there with a Disposition to strike the Sense with the Perception of White, then they could never lose their Whiteness by such Reflexions. I inclined therefore the Paper to the Rays very obliquely, as in the second Experiment of this second Part of the first Book, that the most refrangible Rays, might be more copiously reflected than the rest, and the Whiteness at Length changed successively into blue, indigo, and violet. Then I inclined it the contrary Way, that the least refrangible Rays might be more copious in the reflected Light than the rest, and the Whiteness turned successively to yellow, orange, and red.
Lastly, I made an Instrument XY in fashion of a Comb, whose Teeth being in number sixteen, were about an Inch and a half broad, and the Intervals of the Teeth about two Inches wide. Then by interposing successively the Teeth of this Instrument near the Lens, I intercepted Part of the Colours by the interposed Tooth, whilst the rest of them went on through the Interval of the Teeth to the Paper DE, and there painted a round Solar Image. But the Paper I had first placed so, that the Image might appear white as often as the Comb was taken away; and then the Comb being as was said interposed, that Whiteness by reason of the intercepted Part of the Colours at the Lens did always change into the Colour compounded of those Colours which were not intercepted, and that Colour was by the Motion of the Comb perpetually varied so, that in the passing of every Tooth over the Lens all these Colours, red, yellow, green, blue, and purple, did always succeed one another. I caused therefore all the Teeth to pass successively over the Lens, and when the Motion was slow, there appeared a perpetual Succession of the Colours upon the Paper: But if I so much accelerated the Motion, that the Colours by reason of their quick Succession could not be distinguished from one another, the Appearance of the single Colours ceased. There was no red, no yellow, no green, no blue, nor purple to be seen any longer, but from a Confusion of them all there arose one uniform white Colour. Of the Light which now by the Mixture of all the Colours appeared white, there was no Part really white. One Part was red, another yellow, a third green, a fourth blue, a fifth purple, and every Part retains its proper Colour till it strike the Sensorium. If the Impressions follow one another slowly, so that they may be severally perceived, there is made a distinct Sensation of all the Colours one after another in a continual Succession. But if the Impressions follow one another so quickly, that they cannot be severally perceived, there ariseth out of them all one common Sensation, which is neither of this Colour alone nor of that alone, but hath it self indifferently to ‘em all, and this is a Sensation of Whiteness. By the Quickness of the Successions, the Impressions of the several Colours are confounded in the Sensorium, and out of that Confusion ariseth a mix’d Sensation. If a burning Coal be nimbly moved round in a Circle with Gyrations continually repeated, the whole Circle will appear like Fire; the reason of which is, that the Sensation of the Coal in the several Places of that Circle remains impress’d on the Sensorium, until the Coal return again to the same Place. And so in a quick Consecution of the Colours the Impression of every Colour remains in the Sensorium, until a Revolution of all the Colours be compleated, and that first Colour return again. The Impressions therefore of all the successive Colours are at once in the Sensorium, and jointly stir up a Sensation of them all; and so it is manifest by this Experiment, that the commix’d Impressions of all the Colours do stir up and beget a Sensation of white, that is, that Whiteness is compounded of all the Colours.
And if the Comb be now taken away, that all the Colours may at once pass from the Lens to the Paper, and be there intermixed, and together reflected thence to the Spectator’s Eyes; their Impressions on the Sensorium being now more subtilly and perfectly commixed there, ought much more to stir up a Sensation of Whiteness.
You may instead of the Lens use two Prisms HIK and LMN, which by refracting the coloured Light the contrary Way to that of the first Refraction, may make the diverging Rays converge and meet again in G, as you see represented in the seventh Figure. For where they meet and mix, they will compose a white Light, as when a Lens is used.
Exper. 11. Let the Sun’s coloured Image PT [in Fig. 8.] fall upon the Wall of a dark Chamber, as in the third Experiment of the first Book, and let the same be viewed through a Prism abc, held parallel to the Prism ABC, by whose Refraction that Image was made, and let it now appear lower than before, suppose in the Place S over-against the red Colour T. And if you go near to the Image PT, the Spectrum S will appear oblong and coloured like the Image PT; but if you recede from it, the Colours of the spectrum S will be contracted more and more, and at length vanish, that Spectrum S becoming perfectly round and white; and if you recede yet farther, the Colours will emerge again, but in a contrary Order. Now that Spectrum S appears white in that Case, when the Rays of several sorts which converge from the several Parts of the Image PT, to the Prism abc, are so refracted unequally by it, that in their Passage from the Prism to the Eye they may diverge from one and the same Point of the Spectrum S, and so fall afterwards upon one and the same Point in the bottom of the Eye, and there be mingled.
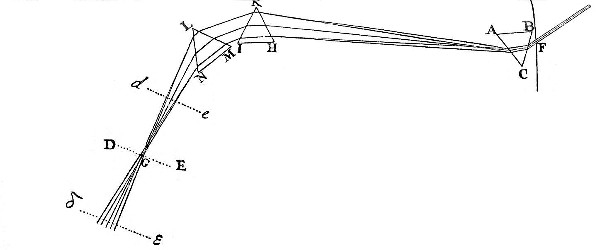Fig. 7.
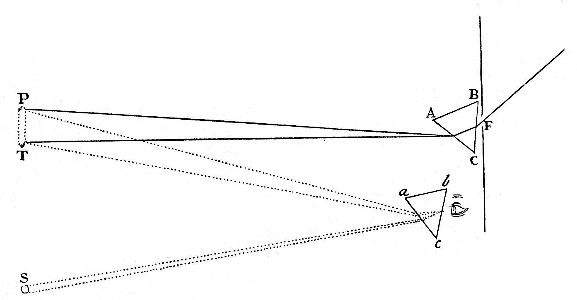Fig. 8.
And farther, if the Comb be here made use of, by whose Teeth the Colours at the Image PT may be successively intercepted; the Spectrum S, when the Comb is moved slowly, will be perpetually tinged with successive Colours: But when by accelerating the Motion of the Comb, the Succession of the Colours is so quick that they cannot be severally seen, that Spectrum S, by a confused and mix’d Sensation of them all, will appear white.
Exper. 12. The Sun shining through a large Prism ABC [in Fig. 9.] upon a Comb XY, placed immediately behind the Prism, his Light which passed through the Interstices of the Teeth fell upon a white Paper DE. The Breadths of the Teeth were equal to their Interstices, and seven Teeth together with their Interstices took up an Inch in Breadth. Now, when the Paper was about two or three Inches distant from the Comb, the Light which passed through its several Interstices painted so many Ranges of Colours, kl, mn, op, qr, &c. which were parallel to one another, and contiguous, and without any Mixture of white. And these Ranges of Colours, if the Comb was moved continually up and down with a reciprocal Motion, ascended and descended in the Paper, and when the Motion of the Comb was so quick, that the Colours could not be distinguished from one another, the whole Paper by their Confusion and Mixture in the Sensorium appeared white.
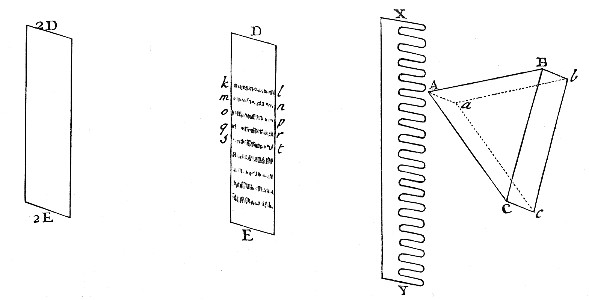Fig. 9.
Let the Comb now rest, and let the Paper be removed farther from the Prism, and the several Ranges of Colours will be dilated and expanded into one another more and more, and by mixing their Colours will dilute one another, and at length, when the distance of the Paper from the Comb is about a Foot, or a little more (suppose in the Place 2D 2E) they will so far dilute one another, as to become white.
With any Obstacle, let all the Light be now stopp’d which passes through any one Interval of the Teeth, so that the Range of Colours which comes from thence may be taken away, and you will see the Light of the rest of the Ranges to be expanded into the Place of the Range taken away, and there to be coloured. Let the intercepted Range pass on as before, and its Colours falling upon the Colours of the other Ranges, and mixing with them, will restore the Whiteness.
Let the Paper 2D 2E be now very much inclined to the Rays, so that the most refrangible Rays may be more copiously reflected than the rest, and the white Colour of the Paper through the Excess of those Rays will be changed into blue and violet. Let the Paper be as much inclined the contrary way, that the least refrangible Rays may be now more copiously reflected than the rest, and by their Excess the Whiteness will be changed into yellow and red. The several Rays therefore in that white Light do retain their colorific Qualities, by which those of any sort, whenever they become more copious than the rest, do by their Excess and Predominance cause their proper Colour to appear.
And by the same way of arguing, applied to the third Experiment of this second Part of the first Book, it may be concluded, that the white Colour of all refracted Light at its very first Emergence, where it appears as white as before its Incidence, is compounded of various Colours.
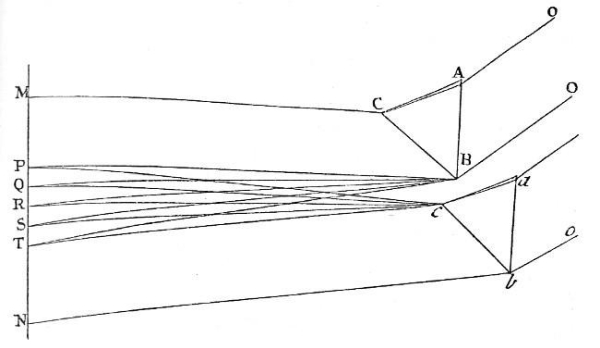Fig. 10.
Exper. 13. In the foregoing Experiment the several Intervals of the Teeth of the Comb do the Office of so many Prisms, every Interval producing the Phænomenon of one Prism. Whence instead of those Intervals using several Prisms, I try’d to compound Whiteness by mixing their Colours, and did it by using only three Prisms, as also by using only two as follows. Let two Prisms ABC and abc, [in Fig. 10.] whose refracting Angles B and b are equal, be so placed parallel to one another, that the refracting Angle B of the one may touch the Angle c at the Base of the other, and their Planes CB and cb, at which the Rays emerge, may lie in Directum. Then let the Light trajected through them fall upon the Paper MN, distant about 8 or 12 Inches from the Prisms. And the Colours generated by the interior Limits B and c of the two Prisms, will be mingled at PT, and there compound white. For if either Prism be taken away, the Colours made by the other will appear in that Place PT, and when the Prism is restored to its Place again, so that its Colours may there fall upon the Colours of the other, the Mixture of them both will restore the Whiteness.
This Experiment succeeds also, as I have tried, when the Angle b of the lower Prism, is a little greater than the Angle B of the upper, and between the interior Angles B and c, there intercedes some Space Bc, as is represented in the Figure, and the refracting Planes BC and bc, are neither in Directum, nor parallel to one another. For there is nothing more requisite to the Success of this Experiment, than that the Rays of all sorts may be uniformly mixed upon the Paper in the Place PT. If the most refrangible Rays coming from the superior Prism take up all the Space from M to P, the Rays of the same sort which come from the inferior Prism ought to begin at P, and take up all the rest of the Space from thence towards N. If the least refrangible Rays coming from the superior Prism take up the Space MT, the Rays of the same kind which come from the other Prism ought to begin at T, and take up the remaining Space TN. If one sort of the Rays which have intermediate Degrees of Refrangibility, and come from the superior Prism be extended through the Space MQ, and another sort of those Rays through the Space MR, and a third sort of them through the Space MS, the same sorts of Rays coming from the lower Prism, ought to illuminate the remaining Spaces QN, RN, SN, respectively. And the same is to be understood of all the other sorts of Rays. For thus the Rays of every sort will be scattered uniformly and evenly through the whole Space MN, and so being every where mix’d in the same Proportion, they must every where produce the same Colour. And therefore, since by this Mixture they produce white in the Exterior Spaces MP and TN, they must also produce white in the Interior Space PT. This is the reason of the Composition by which Whiteness was produced in this Experiment, and by what other way soever I made the like Composition, the Result was Whiteness.
Lastly, If with the Teeth of a Comb of a due Size, the coloured Lights of the two Prisms which fall upon the Space PT be alternately intercepted, that Space PT, when the Motion of the Comb is slow, will always appear coloured, but by accelerating the Motion of the Comb so much that the successive Colours cannot be distinguished from one another, it will appear white.
Exper. 14. Hitherto I have produced Whiteness by mixing the Colours of Prisms. If now the Colours of natural Bodies are to be mingled, let Water a little thicken’d with Soap be agitated to raise a Froth, and after that Froth has stood a little, there will appear to one that shall view it intently various Colours every where in the Surfaces of the several Bubbles; but to one that shall go so far off, that he cannot distinguish the Colours from one another, the whole Froth will grow white with a perfect Whiteness.
Exper. 15. Lastly, In attempting to compound a white, by mixing the coloured Powders which Painters use, I consider’d that all colour’d Powders do suppress and stop in them a very considerable Part of the Light by which they are illuminated. For they become colour’d by reflecting the Light of their own Colours more copiously, and that of all other Colours more sparingly, and yet they do not reflect the Light of their own Colours so copiously as white Bodies do. If red Lead, for instance, and a white Paper, be placed in the red Light of the colour’d Spectrum made in a dark Chamber by the Refraction of a Prism, as is described in the third Experiment of the first Part of this Book; the Paper will appear more lucid than the red Lead, and therefore reflects the red-making Rays more copiously than red Lead doth. And if they be held in the Light of any other Colour, the Light reflected by the Paper will exceed the Light reflected by the red Lead in a much greater Proportion. And the like happens in Powders of other Colours. And therefore by mixing such Powders, we are not to expect a strong and full White, such as is that of Paper, but some dusky obscure one, such as might arise from a Mixture of Light and Darkness, or from white and black, that is, a grey, or dun, or russet brown, such as are the Colours of a Man’s Nail, of a Mouse, of Ashes, of ordinary Stones, of Mortar, of Dust and Dirt in High-ways, and the like. And such a dark white I have often produced by mixing colour’d Powders. For thus one Part of red Lead, and five Parts of Viride Æris, composed a dun Colour like that of a Mouse. For these two Colours were severally so compounded of others, that in both together were a Mixture of all Colours; and there was less red Lead used than Viride Æris, because of the Fulness of its Colour. Again, one Part of red Lead, and four Parts of blue Bise, composed a dun Colour verging a little to purple, and by adding to this a certain Mixture of Orpiment and Viride Æris in a due Proportion, the Mixture lost its purple Tincture, and became perfectly dun. But the Experiment succeeded best without Minium thus. To Orpiment I added by little and little a certain full bright purple, which Painters use, until the Orpiment ceased to be yellow, and became of a pale red. Then I diluted that red by adding a little Viride Æris, and a little more blue Bise than Viride Æris, until it became of such a grey or pale white, as verged to no one of the Colours more than to another. For thus it became of a Colour equal in Whiteness to that of Ashes, or of Wood newly cut, or of a Man’s Skin. The Orpiment reflected more Light than did any other of the Powders, and therefore conduced more to the Whiteness of the compounded Colour than they. To assign the Proportions accurately may be difficult, by reason of the different Goodness of Powders of the same kind. Accordingly, as the Colour of any Powder is more or less full and luminous, it ought to be used in a less or greater Proportion.
Now, considering that these grey and dun Colours may be also produced by mixing Whites and Blacks, and by consequence differ from perfect Whites, not in Species of Colours, but only in degree of Luminousness, it is manifest that there is nothing more requisite to make them perfectly white than to increase their Light sufficiently; and, on the contrary, if by increasing their Light they can be brought to perfect Whiteness, it will thence also follow, that they are of the same Species of Colour with the best Whites, and differ from them only in the Quantity of Light. And this I tried as follows. I took the third of the above-mention’d grey Mixtures, (that which was compounded of Orpiment, Purple, Bise, and Viride Æris) and rubbed it thickly upon the Floor of my Chamber, where the Sun shone upon it through the opened Casement; and by it, in the shadow, I laid a Piece of white Paper of the same Bigness. Then going from them to the distance of 12 or 18 Feet, so that I could not discern the Unevenness of the Surface of the Powder, nor the little Shadows let fall from the gritty Particles thereof; the Powder appeared intensely white, so as to transcend even the Paper it self in Whiteness, especially if the Paper were a little shaded from the Light of the Clouds, and then the Paper compared with the Powder appeared of such a grey Colour as the Powder had done before. But by laying the Paper where the Sun shines through the Glass of the Window, or by shutting the Window that the Sun might shine through the Glass upon the Powder, and by such other fit Means of increasing or decreasing the Lights wherewith the Powder and Paper were illuminated, the Light wherewith the Powder is illuminated may be made stronger in such a due Proportion than the Light wherewith the Paper is illuminated, that they shall both appear exactly alike in Whiteness. For when I was trying this, a Friend coming to visit me, I stopp’d him at the Door, and before I told him what the Colours were, or what I was doing; I asked him, Which of the two Whites were the best, and wherein they differed? And after he had at that distance viewed them well, he answer’d, that they were both good Whites, and that he could not say which was best, nor wherein their Colours differed. Now, if you consider, that this White of the Powder in the Sun-shine was compounded of the Colours which the component Powders (Orpiment, Purple, Bise, and Viride Æris) have in the same Sun-shine, you must acknowledge by this Experiment, as well as by the former, that perfect Whiteness may be compounded of Colours.
From what has been said it is also evident, that the Whiteness of the Sun’s Light is compounded of all the Colours wherewith the several sorts of Rays whereof that Light consists, when by their several Refrangibilities they are separated from one another, do tinge Paper or any other white Body whereon they fall. For those Colours (by Prop. II. Part 2.) are unchangeable, and whenever all those Rays with those their Colours are mix’d again, they reproduce the same white Light as before.
PROP. VI. Prob. II.
In a mixture of Primary Colours, the Quantity and Quality of each being given, to know the Colour of the Compound.
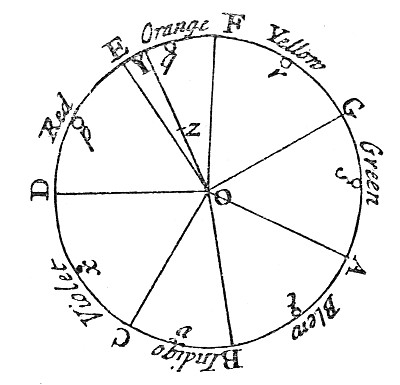Fig. 11.
With the Center O [in Fig. 11.] and Radius OD describe a Circle ADF, and distinguish its Circumference into seven Parts DE, EF, FG, GA, AB, BC, CD, proportional to the seven Musical Tones or Intervals of the eight Sounds, Sol, la, fa, sol, la, mi, fa, sol, contained in an eight, that is, proportional to the Number 1/9, 1/16, 1/10, 1/9, 1/16, 1/16, 1/9. Let the first Part DE represent a red Colour, the second EF orange, the third FG yellow, the fourth CA green, the fifth AB blue, the sixth BC indigo, and the seventh CD violet. And conceive that these are all the Colours of uncompounded Light gradually passing into one another, as they do when made by Prisms; the Circumference DEFGABCD, representing the whole Series of Colours from one end of the Sun’s colour’d Image to the other, so that from D to E be all degrees of red, at E the mean Colour between red and orange, from E to F all degrees of orange, at F the mean between orange and yellow, from F to G all degrees of yellow, and so on. Let p be the Center of Gravity of the Arch DE, and q, r, s, t, u, x, the Centers of Gravity of the Arches EF, FG, GA, AB, BC, and CD respectively, and about those Centers of Gravity let Circles proportional to the Number of Rays of each Colour in the given Mixture be describ’d: that is, the Circle p proportional to the Number of the red-making Rays in the Mixture, the Circle q proportional to the Number of the orange-making Rays in the Mixture, and so of the rest. Find the common Center of Gravity of all those Circles, p, q, r, s, t, u, x. Let that Center be Z; and from the Center of the Circle ADF, through Z to the Circumference, drawing the Right Line OY, the Place of the Point Y in the Circumference shall shew the Colour arising from the Composition of all the Colours in the given Mixture, and the Line OZ shall be proportional to the Fulness or Intenseness of the Colour, that is, to its distance from Whiteness. As if Y fall in the middle between F and G, the compounded Colour shall be the best yellow; if Y verge from the middle towards F or G, the compound Colour shall accordingly be a yellow, verging towards orange or green. If Z fall upon the Circumference, the Colour shall be intense and florid in the highest Degree; if it fall in the mid-way between the Circumference and Center, it shall be but half so intense, that is, it shall be such a Colour as would be made by diluting the intensest yellow with an equal quantity of whiteness; and if it fall upon the center O, the Colour shall have lost all its intenseness, and become a white. But it is to be noted, That if the point Z fall in or near the line OD, the main ingredients being the red and violet, the Colour compounded shall not be any of the prismatick Colours, but a purple, inclining to red or violet, accordingly as the point Z lieth on the side of the line DO towards E or towards C, and in general the compounded violet is more bright and more fiery than the uncompounded. Also if only two of the primary Colours which in the circle are opposite to one another be mixed in an equal proportion, the point Z shall fall upon the center O, and yet the Colour compounded of those two shall not be perfectly white, but some faint anonymous Colour. For I could never yet by mixing only two primary Colours produce a perfect white. Whether it may be compounded of a mixture of three taken at equal distances in the circumference I do not know, but of four or five I do not much question but it may. But these are Curiosities of little or no moment to the understanding the Phænomena of Nature. For in all whites produced by Nature, there uses to be a mixture of all sorts of Rays, and by consequence a composition of all Colours.
To give an instance of this Rule; suppose a Colour is compounded of these homogeneal Colours, of violet one part, of indigo one part, of blue two parts, of green three parts, of yellow five parts, of orange six parts, and of red ten parts. Proportional to these parts describe the Circles x, v, t, s, r, q, p, respectively, that is, so that if the Circle x be one, the Circle v may be one, the Circle t two, the Circle s three, and the Circles r, q and p, five, six and ten. Then I find Z the common center of gravity of these Circles, and through Z drawing the Line OY, the Point Y falls upon the circumference between E and F, something nearer to E than to F, and thence I conclude, that the Colour compounded of these Ingredients will be an orange, verging a little more to red than to yellow. Also I find that OZ is a little less than one half of OY, and thence I conclude, that this orange hath a little less than half the fulness or intenseness of an uncompounded orange; that is to say, that it is such an orange as may be made by mixing an homogeneal orange with a good white in the proportion of the Line OZ to the Line ZY, this Proportion being not of the quantities of mixed orange and white Powders, but of the quantities of the Lights reflected from them.
This Rule I conceive accurate enough for practice, though not mathematically accurate; and the truth of it may be sufficiently proved to Sense, by stopping any of the Colours at the Lens in the tenth Experiment of this Book. For the rest of the Colours which are not stopp’d, but pass on to the Focus of the Lens, will there compound either accurately or very nearly such a Colour, as by this Rule ought to result from their Mixture.
PROP. VII. Theor. V.
All the Colours in the Universe which are made by Light, and depend not on the Power of Imagination, are either the Colours of homogeneal Lights, or compounded of these, and that either accurately or very nearly, according to the Rule of the foregoing Problem.
For it has been proved (in Pro. Part 2.) that the changes of Colours made by Refractions do not arise from any new Modifications of the Rays impress’d by those Refractions, and by the various Terminations of Light and Shadow, as has been the constant and general Opinion of Philosophers. It has also been proved that the several Colours of the homogeneal Rays do constantly answer to their degrees of Refrangibility, (Pro. Part 1. and Pro. Part 2.) and that their degrees of Refrangibility cannot be changed by Refractions and Reflexions (Pro. Part 1.) and by consequence that those their Colours are likewise immutable. It has also been proved directly by refracting and reflecting homogeneal Lights apart, that their Colours cannot be changed, (Pro. Part 2.) It has been proved also, that when the several sorts of Rays are mixed, and in crossing pass through the same space, they do not act on one another so as to change each others colorific qualities. (Exper. 10. Part 2.) but by mixing their Actions in the Sensorium beget a Sensation differing from what either would do apart, that is a Sensation of a mean Colour between their proper Colours; and particularly when by the concourse and mixtures of all sorts of Rays, a white Colour is produced, the white is a mixture of all the Colours which the Rays would have apart, (Pro. Part 2.) The Rays in that mixture do not lose or alter their several colorific qualities, but by all their various kinds of Actions mix’d in the Sensorium, beget a Sensation of a middling Colour between all their Colours, which is whiteness. For whiteness is a mean between all Colours, having it self indifferently to them all, so as with equal facility to be tinged with any of them. A red Powder mixed with a little blue, or a blue with a little red, doth not presently lose its Colour, but a white Powder mix’d with any Colour is presently tinged with that Colour, and is equally capable of being tinged with any Colour whatever. It has been shewed also, that as the Sun’s Light is mix’d of all sorts of Rays, so its whiteness is a mixture of the Colours of all sorts of Rays; those Rays having from the beginning their several colorific qualities as well as their several Refrangibilities, and retaining them perpetually unchanged notwithstanding any Refractions or Reflexions they may at any time suffer, and that whenever any sort of the Sun’s Rays is by any means (as by Reflexion in Exper. 9, and 10. Part 1. or by Refraction as happens in all Refractions) separated from the rest, they then manifest their proper Colours. These things have been prov’d, and the sum of all this amounts to the Proposition here to be proved. For if the Sun’s Light is mix’d of several sorts of Rays, each of which have originally their several Refrangibilities and colorific Qualities, and notwithstanding their Refractions and Reflexions, and their various Separations or Mixtures, keep those their original Properties perpetually the same without alteration; then all the Colours in the World must be such as constantly ought to arise from the original colorific qualities of the Rays whereof the Lights consist by which those Colours are seen. And therefore if the reason of any Colour whatever be required, we have nothing else to do than to consider how the Rays in the Sun’s Light have by Reflexions or Refractions, or other causes, been parted from one another, or mixed together; or otherwise to find out what sorts of Rays are in the Light by which that Colour is made, and in what Proportion; and then by the last Problem to learn the Colour which ought to arise by mixing those Rays (or their Colours) in that proportion. I speak here of Colours so far as they arise from Light. For they appear sometimes by other Causes, as when by the power of Phantasy we see Colours in a Dream, or a Mad-man sees things before him which are not there; or when we see Fire by striking the Eye, or see Colours like the Eye of a Peacock’s Feather, by pressing our Eyes in either corner whilst we look the other way. Where these and such like Causes interpose not, the Colour always answers to the sort or sorts of the Rays whereof the Light consists, as I have constantly found in whatever Phænomena of Colours I have hitherto been able to examine. I shall in the following Propositions give instances of this in the Phænomena of chiefest note.
PROP. VIII. Prob. III.
By the discovered Properties of Light to explain the Colours made by Prisms.
Let ABC [in Fig. 12.] represent a Prism refracting the Light of the Sun, which comes into a dark Chamber through a hole Fφ almost as broad as the Prism, and let MN represent a white Paper on which the refracted Light is cast, and suppose the most refrangible or deepest violet-making Rays fall upon the Space Pπ, the least refrangible or deepest red-making Rays upon the Space Tτ, the middle sort between the indigo-making and blue-making Rays upon the Space Qχ, the middle sort of the green-making Rays upon the Space R, the middle sort between the yellow-making and orange-making Rays upon the Space Sσ, and other intermediate sorts upon intermediate Spaces. For so the Spaces upon which the several sorts adequately fall will by reason of the different Refrangibility of those sorts be one lower than another. Now if the Paper MN be so near the Prism that the Spaces PT and πτ do not interfere with one another, the distance between them Tπ will be illuminated by all the sorts of Rays in that proportion to one another which they have at their very first coming out of the Prism, and consequently be white. But the Spaces PT and πτ on either hand, will not be illuminated by them all, and therefore will appear coloured. And particularly at P, where the outmost violet-making Rays fall alone, the Colour must be the deepest violet. At Q where the violet-making and indigo-making Rays are mixed, it must be a violet inclining much to indigo. At R where the violet-making, indigo-making, blue-making, and one half of the green-making Rays are mixed, their Colours must (by the construction of the second Problem) compound a middle Colour between indigo and blue. At S where all the Rays are mixed, except the red-making and orange-making, their Colours ought by the same Rule to compound a faint blue, verging more to green than indigo. And in the progress from S to T, this blue will grow more and more faint and dilute, till at T, where all the Colours begin to be mixed, it ends in whiteness.
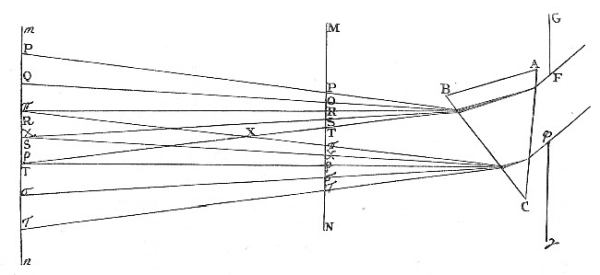Fig. 12.
So again, on the other side of the white at τ, where the least refrangible or utmost red-making Rays are alone, the Colour must be the deepest red. At σ the mixture of red and orange will compound a red inclining to orange. At ρ the mixture of red, orange, yellow, and one half of the green must compound a middle Colour between orange and yellow. At χ the mixture of all Colours but violet and indigo will compound a faint yellow, verging more to green than to orange. And this yellow will grow more faint and dilute continually in its progress from χ to π, where by a mixture of all sorts of Rays it will become white.
These Colours ought to appear were the Sun’s Light perfectly white: But because it inclines to yellow, the Excess of the yellow-making Rays whereby ’tis tinged with that Colour, being mixed with the faint blue between S and T, will draw it to a faint green. And so the Colours in order from P to τ ought to be violet, indigo, blue, very faint green, white, faint yellow, orange, red. Thus it is by the computation: And they that please to view the Colours made by a Prism will find it so in Nature.
These are the Colours on both sides the white when the Paper is held between the Prism and the Point X where the Colours meet, and the interjacent white vanishes. For if the Paper be held still farther off from the Prism, the most refrangible and least refrangible Rays will be wanting in the middle of the Light, and the rest of the Rays which are found there, will by mixture produce a fuller green than before. Also the yellow and blue will now become less compounded, and by consequence more intense than before. And this also agrees with experience.
And if one look through a Prism upon a white Object encompassed with blackness or darkness, the reason of the Colours arising on the edges is much the same, as will appear to one that shall a little consider it. If a black Object be encompassed with a white one, the Colours which appear through the Prism are to be derived from the Light of the white one, spreading into the Regions of the black, and therefore they appear in a contrary order to that, when a white Object is surrounded with black. And the same is to be understood when an Object is viewed, whose parts are some of them less luminous than others. For in the borders of the more and less luminous Parts, Colours ought always by the same Principles to arise from the Excess of the Light of the more luminous, and to be of the same kind as if the darker parts were black, but yet to be more faint and dilute.
What is said of Colours made by Prisms may be easily applied to Colours made by the Glasses of Telescopes or Microscopes, or by the Humours of the Eye. For if the Object-glass of a Telescope be thicker on one side than on the other, or if one half of the Glass, or one half of the Pupil of the Eye be cover’d with any opake substance; the Object-glass, or that part of it or of the Eye which is not cover’d, may be consider’d as a Wedge with crooked Sides, and every Wedge of Glass or other pellucid Substance has the effect of a Prism in refracting the Light which passes through it.[L]
How the Colours in the ninth and tenth Experiments of the first Part arise from the different Reflexibility of Light, is evident by what was there said. But it is observable in the ninth Experiment, that whilst the Sun’s direct Light is yellow, the Excess of the blue-making Rays in the reflected beam of Light MN, suffices only to bring that yellow to a pale white inclining to blue, and not to tinge it with a manifestly blue Colour. To obtain therefore a better blue, I used instead of the yellow Light of the Sun the white Light of the Clouds, by varying a little the Experiment, as follows.
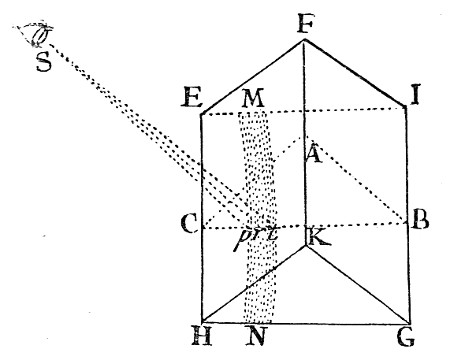Fig. 13.
Exper. 16 Let HFG [in Fig. 13.] represent a Prism in the open Air, and S the Eye of the Spectator, viewing the Clouds by their Light coming into the Prism at the Plane Side FIGK, and reflected in it by its Base HEIG, and thence going out through its Plane Side HEFK to the Eye. And when the Prism and Eye are conveniently placed, so that the Angles of Incidence and Reflexion at the Base may be about 40 Degrees, the Spectator will see a Bow MN of a blue Colour, running from one End of the Base to the other, with the Concave Side towards him, and the Part of the Base IMNG beyond this Bow will be brighter than the other Part EMNH on the other Side of it. This blue Colour MN being made by nothing else than by Reflexion of a specular Superficies, seems so odd a Phænomenon, and so difficult to be explained by the vulgar Hypothesis of Philosophers, that I could not but think it deserved to be taken Notice of. Now for understanding the Reason of it, suppose the Plane ABC to cut the Plane Sides and Base of the Prism perpendicularly. From the Eye to the Line BC, wherein that Plane cuts the Base, draw the Lines Sp and St, in the Angles Spc 50 degr. 1/9, and Stc 49 degr. 1/28, and the Point p will be the Limit beyond which none of the most refrangible Rays can pass through the Base of the Prism, and be refracted, whose Incidence is such that they may be reflected to the Eye; and the Point t will be the like Limit for the least refrangible Rays, that is, beyond which none of them can pass through the Base, whose Incidence is such that by Reflexion they may come to the Eye. And the Point r taken in the middle Way between p and t, will be the like Limit for the meanly refrangible Rays. And therefore all the least refrangible Rays which fall upon the Base beyond t, that is, between t and B, and can come from thence to the Eye, will be reflected thither: But on this side t, that is, between t and c, many of these Rays will be transmitted through the Base. And all the most refrangible Rays which fall upon the Base beyond p, that is, between, p and B, and can by Reflexion come from thence to the Eye, will be reflected thither, but every where between p and c, many of these Rays will get through the Base, and be refracted; and the same is to be understood of the meanly refrangible Rays on either side of the Point r. Whence it follows, that the Base of the Prism must every where between t and B, by a total Reflexion of all sorts of Rays to the Eye, look white and bright. And every where between p and C, by reason of the Transmission of many Rays of every sort, look more pale, obscure, and dark. But at r, and in other Places between p and t, where all the more refrangible Rays are reflected to the Eye, and many of the less refrangible are transmitted, the Excess of the most refrangible in the reflected Light will tinge that Light with their Colour, which is violet and blue. And this happens by taking the Line C prt B any where between the Ends of the Prism HG and EI.
PROP. IX. Prob. IV.
By the discovered Properties of Light to explain the Colours of the Rain-bow.
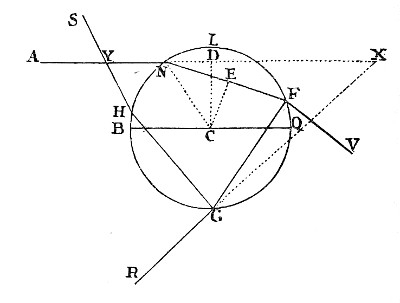Fig. 14.
This Bow never appears, but where it rains in the Sun-shine, and may be made artificially by spouting up Water which may break aloft, and scatter into Drops, and fall down like Rain. For the Sun shining upon these Drops certainly causes the Bow to appear to a Spectator standing in a due Position to the Rain and Sun. And hence it is now agreed upon, that this Bow is made by Refraction of the Sun’s Light in drops of falling Rain. This was understood by some of the Antients, and of late more fully discover’d and explain’d by the famous Antonius de Dominis Archbishop of Spalato, in his book De Radiis Visûs & Lucis, published by his Friend Bartolus at Venice, in the Year 1611, and written above 20 Years before. For he teaches there how the interior Bow is made in round Drops of Rain by two Refractions of the Sun’s Light, and one Reflexion between them, and the exterior by two Refractions, and two sorts of Reflexions between them in each Drop of Water, and proves his Explications by Experiments made with a Phial full of Water, and with Globes of Glass filled with Water, and placed in the Sun to make the Colours of the two Bows appear in them. The same Explication Des-Cartes hath pursued in his Meteors, and mended that of the exterior Bow. But whilst they understood not the true Origin of Colours, it’s necessary to pursue it here a little farther. For understanding therefore how the Bow is made, let a Drop of Rain, or any other spherical transparent Body be represented by the Sphere BNFG, [in Fig. 14.] described with the Center C, and Semi-diameter CN. And let AN be one of the Sun’s Rays incident upon it at N, and thence refracted to F, where let it either go out of the Sphere by Refraction towards V, or be reflected to G; and at G let it either go out by Refraction to R, or be reflected to H; and at H let it go out by Refraction towards S, cutting the incident Ray in Y. Produce AN and RG, till they meet in X, and upon AX and NF, let fall the Perpendiculars CD and CE, and produce CD till it fall upon the Circumference at L. Parallel to the incident Ray AN draw the Diameter BQ, and let the Sine of Incidence out of Air into Water be to the Sine of Refraction as I to R. Now, if you suppose the Point of Incidence N to move from the Point B, continually till it come to L, the Arch QF will first increase and then decrease, and so will the Angle AXR which the Rays AN and GR contain; and the Arch QF and Angle AXR will be biggest when ND is to CN as √(II - RR) to √(3)RR, in which case NE will be to ND as 2R to I. Also the Angle AYS, which the Rays AN and HS contain will first decrease, and then increase and grow least when ND is to CN as √(II - RR) to √(8)RR, in which case NE will be to ND, as 3R to I. And so the Angle which the next emergent Ray (that is, the emergent Ray after three Reflexions) contains with the incident Ray AN will come to its Limit when ND is to CN as √(II - RR) to √(15)RR, in which case NE will be to ND as 4R to I. And the Angle which the Ray next after that Emergent, that is, the Ray emergent after four Reflexions, contains with the Incident, will come to its Limit, when ND is to CN as √(II - RR) to √(24)RR, in which case NE will be to ND as 5R to I; and so on infinitely, the Numbers 3, 8, 15, 24, &c. being gather’d by continual Addition of the Terms of the arithmetical Progression 3, 5, 7, 9, &c. The Truth of all this Mathematicians will easily examine.[M]
Now it is to be observed, that as when the Sun comes to his Tropicks, Days increase and decrease but a very little for a great while together; so when by increasing the distance CD, these Angles come to their Limits, they vary their quantity but very little for some time together, and therefore a far greater number of the Rays which fall upon all the Points N in the Quadrant BL, shall emerge in the Limits of these Angles, than in any other Inclinations. And farther it is to be observed, that the Rays which differ in Refrangibility will have different Limits of their Angles of Emergence, and by consequence according to their different Degrees of Refrangibility emerge most copiously in different Angles, and being separated from one another appear each in their proper Colours. And what those Angles are may be easily gather’d from the foregoing Theorem by Computation.
For in the least refrangible Rays the Sines I and R (as was found above) are 108 and 81, and thence by Computation the greatest Angle AXR will be found 42 Degrees and 2 Minutes, and the least Angle AYS, 50 Degrees and 57 Minutes. And in the most refrangible Rays the Sines I and R are 109 and 81, and thence by Computation the greatest Angle AXR will be found 40 Degrees and 17 Minutes, and the least Angle AYS 54 Degrees and 7 Minutes.
Suppose now that O [in Fig. 15.] is the Spectator’s Eye, and OP a Line drawn parallel to the Sun’s Rays and let POE, POF, POG, POH, be Angles of 40 Degr. 17 Min. 42 Degr. 2 Min. 50 Degr. 57 Min. and 54 Degr. 7 Min. respectively, and these Angles turned about their common Side OP, shall with their other Sides OE, OF; OG, OH, describe the Verges of two Rain-bows AF, BE and CHDG. For if E, F, G, H, be drops placed any where in the conical Superficies described by OE, OF, OG, OH, and be illuminated by the Sun’s Rays SE, SF, SG, SH; the Angle SEO being equal to the Angle POE, or 40 Degr. 17 Min. shall be the greatest Angle in which the most refrangible Rays can after one Reflexion be refracted to the Eye, and therefore all the Drops in the Line OE shall send the most refrangible Rays most copiously to the Eye, and thereby strike the Senses with the deepest violet Colour in that Region. And in like manner the Angle SFO being equal to the Angle POF, or 42 Degr. 2 Min. shall be the greatest in which the least refrangible Rays after one Reflexion can emerge out of the Drops, and therefore those Rays shall come most copiously to the Eye from the Drops in the Line OF, and strike the Senses with the deepest red Colour in that Region. And by the same Argument, the Rays which have intermediate Degrees of Refrangibility shall come most copiously from Drops between E and F, and strike the Senses with the intermediate Colours, in the Order which their Degrees of Refrangibility require, that is in the Progress from E to F, or from the inside of the Bow to the outside in this order, violet, indigo, blue, green, yellow, orange, red. But the violet, by the mixture of the white Light of the Clouds, will appear faint and incline to purple.
Fig. 15.
Again, the Angle SGO being equal to the Angle POG, or 50 Gr. 51 Min. shall be the least Angle in which the least refrangible Rays can after two Reflexions emerge out of the Drops, and therefore the least refrangible Rays shall come most copiously to the Eye from the Drops in the Line OG, and strike the Sense with the deepest red in that Region. And the Angle SHO being equal to the Angle POH, or 54 Gr. 7 Min. shall be the least Angle, in which the most refrangible Rays after two Reflexions can emerge out of the Drops; and therefore those Rays shall come most copiously to the Eye from the Drops in the Line OH, and strike the Senses with the deepest violet in that Region. And by the same Argument, the Drops in the Regions between G and H shall strike the Sense with the intermediate Colours in the Order which their Degrees of Refrangibility require, that is, in the Progress from G to H, or from the inside of the Bow to the outside in this order, red, orange, yellow, green, blue, indigo, violet. And since these four Lines OE, OF, OG, OH, may be situated any where in the above-mention’d conical Superficies; what is said of the Drops and Colours in these Lines is to be understood of the Drops and Colours every where in those Superficies.
Thus shall there be made two Bows of Colours, an interior and stronger, by one Reflexion in the Drops, and an exterior and fainter by two; for the Light becomes fainter by every Reflexion. And their Colours shall lie in a contrary Order to one another, the red of both Bows bordering upon the Space GF, which is between the Bows. The Breadth of the interior Bow EOF measured cross the Colours shall be 1 Degr. 45 Min. and the Breadth of the exterior GOH shall be 3 Degr. 10 Min. and the distance between them GOF shall be 8 Gr. 15 Min. the greatest Semi-diameter of the innermost, that is, the Angle POF being 42 Gr. 2 Min. and the least Semi-diameter of the outermost POG, being 50 Gr. 57 Min. These are the Measures of the Bows, as they would be were the Sun but a Point; for by the Breadth of his Body, the Breadth of the Bows will be increased, and their Distance decreased by half a Degree, and so the breadth of the interior Iris will be 2 Degr. 15 Min. that of the exterior 3 Degr. 40 Min. their distance 8 Degr. 25 Min. the greatest Semi-diameter of the interior Bow 42 Degr. 17 Min. and the least of the exterior 50 Degr. 42 Min. And such are the Dimensions of the Bows in the Heavens found to be very nearly, when their Colours appear strong and perfect. For once, by such means as I then had, I measured the greatest Semi-diameter of the interior Iris about 42 Degrees, and the breadth of the red, yellow and green in that Iris 63 or 64 Minutes, besides the outmost faint red obscured by the brightness of the Clouds, for which we may allow 3 or 4 Minutes more. The breadth of the blue was about 40 Minutes more besides the violet, which was so much obscured by the brightness of the Clouds, that I could not measure its breadth. But supposing the breadth of the blue and violet together to equal that of the red, yellow and green together, the whole breadth of this Iris will be about 2-1/4 Degrees, as above. The least distance between this Iris and the exterior Iris was about 8 Degrees and 30 Minutes. The exterior Iris was broader than the interior, but so faint, especially on the blue side, that I could not measure its breadth distinctly. At another time when both Bows appeared more distinct, I measured the breadth of the interior Iris 2 Gr. 10´, and the breadth of the red, yellow and green in the exterior Iris, was to the breadth of the same Colours in the interior as 3 to 2.
This Explication of the Rain-bow is yet farther confirmed by the known Experiment (made by Antonius de Dominis and Des-Cartes) of hanging up any where in the Sun-shine a Glass Globe filled with Water, and viewing it in such a posture, that the Rays which come from the Globe to the Eye may contain with the Sun’s Rays an Angle of either 42 or 50 Degrees. For if the Angle be about 42 or 43 Degrees, the Spectator (suppose at O) shall see a full red Colour in that side of the Globe opposed to the Sun as ’tis represented at F, and if that Angle become less (suppose by depressing the Globe to E) there will appear other Colours, yellow, green and blue successive in the same side of the Globe. But if the Angle be made about 50 Degrees (suppose by lifting up the Globe to G) there will appear a red Colour in that side of the Globe towards the Sun, and if the Angle be made greater (suppose by lifting up the Globe to H) the red will turn successively to the other Colours, yellow, green and blue. The same thing I have tried, by letting a Globe rest, and raising or depressing the Eye, or otherwise moving it to make the Angle of a just magnitude.
I have heard it represented, that if the Light of a Candle be refracted by a Prism to the Eye; when the blue Colour falls upon the Eye, the Spectator shall see red in the Prism, and when the red falls upon the Eye he shall see blue; and if this were certain, the Colours of the Globe and Rain-bow ought to appear in a contrary order to what we find. But the Colours of the Candle being very faint, the mistake seems to arise from the difficulty of discerning what Colours fall on the Eye. For, on the contrary, I have sometimes had occasion to observe in the Sun’s Light refracted by a Prism, that the Spectator always sees that Colour in the Prism which falls upon his Eye. And the same I have found true also in Candle-light. For when the Prism is moved slowly from the Line which is drawn directly from the Candle to the Eye, the red appears first in the Prism and then the blue, and therefore each of them is seen when it falls upon the Eye. For the red passes over the Eye first, and then the blue.
The Light which comes through drops of Rain by two Refractions without any Reflexion, ought to appear strongest at the distance of about 26 Degrees from the Sun, and to decay gradually both ways as the distance from him increases and decreases. And the same is to be understood of Light transmitted through spherical Hail-stones. And if the Hail be a little flatted, as it often is, the Light transmitted may grow so strong at a little less distance than that of 26 Degrees, as to form a Halo about the Sun or Moon; which Halo, as often as the Hail-stones are duly figured may be colour’d, and then it must be red within by the least refrangible Rays, and blue without by the most refrangible ones, especially if the Hail-stones have opake Globules of Snow in their center to intercept the Light within the Halo (as Hugenius has observ’d) and make the inside thereof more distinctly defined than it would otherwise be. For such Hail-stones, though spherical, by terminating the Light by the Snow, may make a Halo red within and colourless without, and darker in the red than without, as Halos used to be. For of those Rays which pass close by the Snow the Rubriform will be least refracted, and so come to the Eye in the directest Lines.
The Light which passes through a drop of Rain after two Refractions, and three or more Reflexions, is scarce strong enough to cause a sensible Bow; but in those Cylinders of Ice by which Hugenius explains the Parhelia, it may perhaps be sensible.
PROP. X. Prob. V.
By the discovered Properties of Light to explain the permanent Colours of Natural Bodies.
These Colours arise from hence, that some natural Bodies reflect some sorts of Rays, others other sorts more copiously than the rest. Minium reflects the least refrangible or red-making Rays most copiously, and thence appears red. Violets reflect the most refrangible most copiously, and thence have their Colour, and so of other Bodies. Every Body reflects the Rays of its own Colour more copiously than the rest, and from their excess and predominance in the reflected Light has its Colour.
Exper. 17. For if in the homogeneal Lights obtained by the solution of the Problem proposed in the fourth Proposition of the first Part of this Book, you place Bodies of several Colours, you will find, as I have done, that every Body looks most splendid and luminous in the Light of its own Colour. Cinnaber in the homogeneal red Light is most resplendent, in the green Light it is manifestly less resplendent, and in the blue Light still less. Indigo in the violet blue Light is most resplendent, and its splendor is gradually diminish’d, as it is removed thence by degrees through the green and yellow Light to the red. By a Leek the green Light, and next that the blue and yellow which compound green, are more strongly reflected than the other Colours red and violet, and so of the rest. But to make these Experiments the more manifest, such Bodies ought to be chosen as have the fullest and most vivid Colours, and two of those Bodies are to be compared together. Thus, for instance, if Cinnaber and ultra-marine blue, or some other full blue be held together in the red homogeneal Light, they will both appear red, but the Cinnaber will appear of a strongly luminous and resplendent red, and the ultra-marine blue of a faint obscure and dark red; and if they be held together in the blue homogeneal Light, they will both appear blue, but the ultra-marine will appear of a strongly luminous and resplendent blue, and the Cinnaber of a faint and dark blue. Which puts it out of dispute that the Cinnaber reflects the red Light much more copiously than the ultra-marine doth, and the ultra-marine reflects the blue Light much more copiously than the Cinnaber doth. The same Experiment may be tried successfully with red Lead and Indigo, or with any other two colour’d Bodies, if due allowance be made for the different strength or weakness of their Colour and Light.
And as the reason of the Colours of natural Bodies is evident by these Experiments, so it is farther confirmed and put past dispute by the two first Experiments of the first Part, whereby ’twas proved in such Bodies that the reflected Lights which differ in Colours do differ also in degrees of Refrangibility. For thence it’s certain, that some Bodies reflect the more refrangible, others the less refrangible Rays more copiously.
And that this is not only a true reason of these Colours, but even the only reason, may appear farther from this Consideration, that the Colour of homogeneal Light cannot be changed by the Reflexion of natural Bodies.
For if Bodies by Reflexion cannot in the least change the Colour of any one sort of Rays, they cannot appear colour’d by any other means than by reflecting those which either are of their own Colour, or which by mixture must produce it.
But in trying Experiments of this kind care must be had that the Light be sufficiently homogeneal. For if Bodies be illuminated by the ordinary prismatick Colours, they will appear neither of their own Day-light Colours, nor of the Colour of the Light cast on them, but of some middle Colour between both, as I have found by Experience. Thus red Lead (for instance) illuminated with the ordinary prismatick green will not appear either red or green, but orange or yellow, or between yellow and green, accordingly as the green Light by which ’tis illuminated is more or less compounded. For because red Lead appears red when illuminated with white Light, wherein all sorts of Rays are equally mix’d, and in the green Light all sorts of Rays are not equally mix’d, the Excess of the yellow-making, green-making and blue-making Rays in the incident green Light, will cause those Rays to abound so much in the reflected Light, as to draw the Colour from red towards their Colour. And because the red Lead reflects the red-making Rays most copiously in proportion to their number, and next after them the orange-making and yellow-making Rays; these Rays in the reflected Light will be more in proportion to the Light than they were in the incident green Light, and thereby will draw the reflected Light from green towards their Colour. And therefore the red Lead will appear neither red nor green, but of a Colour between both.
In transparently colour’d Liquors ’tis observable, that their Colour uses to vary with their thickness. Thus, for instance, a red Liquor in a conical Glass held between the Light and the Eye, looks of a pale and dilute yellow at the bottom where ’tis thin, and a little higher where ’tis thicker grows orange, and where ’tis still thicker becomes red, and where ’tis thickest the red is deepest and darkest. For it is to be conceiv’d that such a Liquor stops the indigo-making and violet-making Rays most easily, the blue-making Rays more difficultly, the green-making Rays still more difficultly, and the red-making most difficultly: And that if the thickness of the Liquor be only so much as suffices to stop a competent number of the violet-making and indigo-making Rays, without diminishing much the number of the rest, the rest must (by Pro. Part 2.) compound a pale yellow. But if the Liquor be so much thicker as to stop also a great number of the blue-making Rays, and some of the green-making, the rest must compound an orange; and where it is so thick as to stop also a great number of the green-making and a considerable number of the yellow-making, the rest must begin to compound a red, and this red must grow deeper and darker as the yellow-making and orange-making Rays are more and more stopp’d by increasing the thickness of the Liquor, so that few Rays besides the red-making can get through.
Of this kind is an Experiment lately related to me by Mr. Halley, who, in diving deep into the Sea in a diving Vessel, found in a clear Sun-shine Day, that when he was sunk many Fathoms deep into the Water the upper part of his Hand on which the Sun shone directly through the Water and through a small Glass Window in the Vessel appeared of a red Colour, like that of a Damask Rose, and the Water below and the under part of his Hand illuminated by Light reflected from the Water below look’d green. For thence it may be gather’d, that the Sea-Water reflects back the violet and blue-making Rays most easily, and lets the red-making Rays pass most freely and copiously to great Depths. For thereby the Sun’s direct Light at all great Depths, by reason of the predominating red-making Rays, must appear red; and the greater the Depth is, the fuller and intenser must that red be. And at such Depths as the violet-making Rays scarce penetrate unto, the blue-making, green-making, and yellow-making Rays being reflected from below more copiously than the red-making ones, must compound a green.
Now, if there be two Liquors of full Colours, suppose a red and blue, and both of them so thick as suffices to make their Colours sufficiently full; though either Liquor be sufficiently transparent apart, yet will you not be able to see through both together. For, if only the red-making Rays pass through one Liquor, and only the blue-making through the other, no Rays can pass through both. This Mr. Hook tried casually with Glass Wedges filled with red and blue Liquors, and was surprized at the unexpected Event, the reason of it being then unknown; which makes me trust the more to his Experiment, though I have not tried it my self. But he that would repeat it, must take care the Liquors be of very good and full Colours.
Now, whilst Bodies become coloured by reflecting or transmitting this or that sort of Rays more copiously than the rest, it is to be conceived that they stop and stifle in themselves the Rays which they do not reflect or transmit. For, if Gold be foliated and held between your Eye and the Light, the Light looks of a greenish blue, and therefore massy Gold lets into its Body the blue-making Rays to be reflected to and fro within it till they be stopp’d and stifled, whilst it reflects the yellow-making outwards, and thereby looks yellow. And much after the same manner that Leaf Gold is yellow by reflected, and blue by transmitted Light, and massy Gold is yellow in all Positions of the Eye; there are some Liquors, as the Tincture of Lignum Nephriticum, and some sorts of Glass which transmit one sort of Light most copiously, and reflect another sort, and thereby look of several Colours, according to the Position of the Eye to the Light. But, if these Liquors or Glasses were so thick and massy that no Light could get through them, I question not but they would like all other opake Bodies appear of one and the same Colour in all Positions of the Eye, though this I cannot yet affirm by Experience. For all colour’d Bodies, so far as my Observation reaches, may be seen through if made sufficiently thin, and therefore are in some measure transparent, and differ only in degrees of Transparency from tinged transparent Liquors; these Liquors, as well as those Bodies, by a sufficient Thickness becoming opake. A transparent Body which looks of any Colour by transmitted Light, may also look of the same Colour by reflected Light, the Light of that Colour being reflected by the farther Surface of the Body, or by the Air beyond it. And then the reflected Colour will be diminished, and perhaps cease, by making the Body very thick, and pitching it on the backside to diminish the Reflexion of its farther Surface, so that the Light reflected from the tinging Particles may predominate. In such Cases, the Colour of the reflected Light will be apt to vary from that of the Light transmitted. But whence it is that tinged Bodies and Liquors reflect some sort of Rays, and intromit or transmit other sorts, shall be said in the next Book. In this Proposition I content my self to have put it past dispute, that Bodies have such Properties, and thence appear colour’d.
PROP. XI. Prob. VI.
By mixing colour’d Lights to compound a beam of Light of the same Colour and Nature with a beam of the Sun’s direct Light, and therein to experience the Truth of the foregoing Propositions.
Fig. 16.
Let ABC abc [in Fig. 16.] represent a Prism, by which the Sun’s Light let into a dark Chamber through the Hole F, may be refracted towards the Lens MN, and paint upon it at p, q, r, s, and t, the usual Colours violet, blue, green, yellow, and red, and let the diverging Rays by the Refraction of this Lens converge again towards X, and there, by the mixture of all those their Colours, compound a white according to what was shewn above. Then let another Prism DEG deg, parallel to the former, be placed at X, to refract that white Light upwards towards Y. Let the refracting Angles of the Prisms, and their distances from the Lens be equal, so that the Rays which converged from the Lens towards X, and without Refraction, would there have crossed and diverged again, may by the Refraction of the second Prism be reduced into Parallelism and diverge no more. For then those Rays will recompose a beam of white Light XY. If the refracting Angle of either Prism be the bigger, that Prism must be so much the nearer to the Lens. You will know when the Prisms and the Lens are well set together, by observing if the beam of Light XY, which comes out of the second Prism be perfectly white to the very edges of the Light, and at all distances from the Prism continue perfectly and totally white like a beam of the Sun’s Light. For till this happens, the Position of the Prisms and Lens to one another must be corrected; and then if by the help of a long beam of Wood, as is represented in the Figure, or by a Tube, or some other such Instrument, made for that Purpose, they be made fast in that Situation, you may try all the same Experiments in this compounded beam of Light XY, which have been made in the Sun’s direct Light. For this compounded beam of Light has the same appearance, and is endow’d with all the same Properties with a direct beam of the Sun’s Light, so far as my Observation reaches. And in trying Experiments in this beam you may by stopping any of the Colours, p, q, r, s, and t, at the Lens, see how the Colours produced in the Experiments are no other than those which the Rays had at the Lens before they entered the Composition of this Beam: And by consequence, that they arise not from any new Modifications of the Light by Refractions and Reflexions, but from the various Separations and Mixtures of the Rays originally endow’d with their colour-making Qualities.
So, for instance, having with a Lens 4-1/4 Inches broad, and two Prisms on either hand 6-1/4 Feet distant from the Lens, made such a beam of compounded Light; to examine the reason of the Colours made by Prisms, I refracted this compounded beam of Light XY with another Prism HIK kh, and thereby cast the usual Prismatick Colours PQRST upon the Paper LV placed behind. And then by stopping any of the Colours p, q, r, s, t, at the Lens, I found that the same Colour would vanish at the Paper. So if the Purple p was stopp’d at the Lens, the Purple P upon the Paper would vanish, and the rest of the Colours would remain unalter’d, unless perhaps the blue, so far as some purple latent in it at the Lens might be separated from it by the following Refractions. And so by intercepting the green upon the Lens, the green R upon the Paper would vanish, and so of the rest; which plainly shews, that as the white beam of Light XY was compounded of several Lights variously colour’d at the Lens, so the Colours which afterwards emerge out of it by new Refractions are no other than those of which its Whiteness was compounded. The Refraction of the Prism HIK kh generates the Colours PQRST upon the Paper, not by changing the colorific Qualities of the Rays, but by separating the Rays which had the very same colorific Qualities before they enter’d the Composition of the refracted beam of white Light XY. For otherwise the Rays which were of one Colour at the Lens might be of another upon the Paper, contrary to what we find.
So again, to examine the reason of the Colours of natural Bodies, I placed such Bodies in the Beam of Light XY, and found that they all appeared there of those their own Colours which they have in Day-light, and that those Colours depend upon the Rays which had the same Colours at the Lens before they enter’d the Composition of that beam. Thus, for instance, Cinnaber illuminated by this beam appears of the same red Colour as in Day-light; and if at the Lens you intercept the green-making and blue-making Rays, its redness will become more full and lively: But if you there intercept the red-making Rays, it will not any longer appear red, but become yellow or green, or of some other Colour, according to the sorts of Rays which you do not intercept. So Gold in this Light XY appears of the same yellow Colour as in Day-light, but by intercepting at the Lens a due Quantity of the yellow-making Rays it will appear white like Silver (as I have tried) which shews that its yellowness arises from the Excess of the intercepted Rays tinging that Whiteness with their Colour when they are let pass. So the Infusion of Lignum Nephriticum (as I have also tried) when held in this beam of Light XY, looks blue by the reflected Part of the Light, and red by the transmitted Part of it, as when ’tis view’d in Day-light; but if you intercept the blue at the Lens the Infusion will lose its reflected blue Colour, whilst its transmitted red remains perfect, and by the loss of some blue-making Rays, wherewith it was allay’d, becomes more intense and full. And, on the contrary, if the red and orange-making Rays be intercepted at the Lens, the Infusion will lose its transmitted red, whilst its blue will remain and become more full and perfect. Which shews, that the Infusion does not tinge the Rays with blue and red, but only transmits those most copiously which were red-making before, and reflects those most copiously which were blue-making before. And after the same manner may the Reasons of other Phænomena be examined, by trying them in this artificial beam of Light XY.
FOOTNOTES:
[J] See our Author’s Lect. Optic. Part II. Sect. II. .
[K] As is done in our Author’s Lect. Optic. Part I. Sect. III. and IV. and Part II. Sect. II.
[L] See our Author’s Lect. Optic. Part II. Sect. II. pag. 269, &c.
[M] This is demonstrated in our Author’s Lect. Optic. Part I. Sect. IV. Pro and 36.