Beyond the Sigmoid
There is no such thing as a perfect replacement for the sigmoid. Different activation functions work well in different circumstances, and researchers keep coming up with brand-new ones. That being said, one activation function has proven so broadly useful that it’s become a default of sorts. Let’s talk about it.
Enter the ReLU
The go-to replacement for the sigmoid these days is the rectified linear unit, or ReLU for friends. Compared with the sigmoid, the ReLU is surprisingly simple. Here’s a Python implementation of it:
| | def relu(z): |
| | if z <= 0: |
| | return 0 |
| | else: |
| | return z |
And the following diagram illustrates what it looks like:
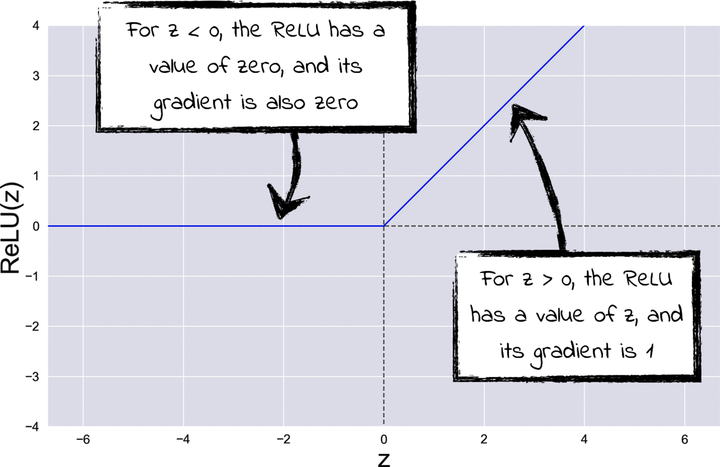
The ReLU is composed of two straight segments. However, taken together they add up to a nonlinear function, like a good activation function should be.
The ReLU may be simple, but it’s all the better for it. Computing its gradient is cheap, which makes for fast training. The ReLU’s killer feature, however, is that gradient of 1 for positive inputs. When backpropagation passes through a ReLU with a positive input, the global gradient is multiplied by 1, so it doesn’t change at all. That detail alone solves the problem of vanishing gradients for good.
While the ReLU gingerly steps around vanishing gradients, it does nothing to solve dead neurons. On the contrary, it seems to have this issue even more than the sigmoid, because it flatlines with negative inputs. On a ReLU with a negative input, GD gets stuck on a gradient of zero, with no hope of ever leaving it. Isn’t that a recipe for disaster?
As it turns out, that’s not necessarily the case. In some cases, dead ReLUs might even be beneficial to a neural network. Researchers have stumbled on a counterintuitive result: sometimes, dead ReLUs can make training faster and more effective, because they help the network ignore irrelevant information.
That being said, there is no doubt that too many dead ReLUs can disrupt a neural network. If you suspect that’s happening in your own network, you can replace the ReLU with its souped-up sibling, the Leaky ReLU, which is illustrated in the graph.
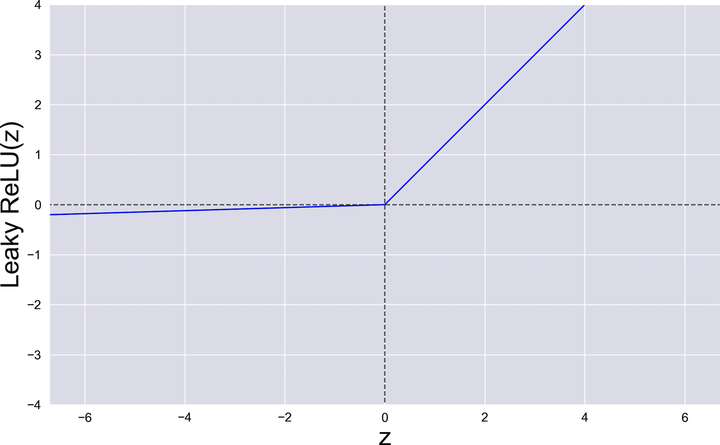
Did you spot the difference between the Leaky ReLU and the ReLU? Instead of going flat for negative values, the Leaky ReLU is slightly sloped. That constant slope guarantees that the gradient never becomes zero, and the neurons in the network never die. When you use a Leaky ReLU in a library such as Keras, you can change its slope, so that’s one more hyperparameter that you can tune.
Finally, you might have noticed a blemish in the ReLU family. I said that a good activation function should be smooth—otherwise, you cannot calculate its gradient. But the ReLU and the Leaky ReLU aren’t smooth: they have a cusp at the value of 0. Won’t that cusp trip up GD?
That turns out not to be a problem in practice. From a mathematical standpoint, it’s true that the ReLU’s gradient is technically undefined at z = 0. However, ReLU implementations are only too happy to shrug off mathematical purity, and return a gradient of either 0 or 1 if their input happens to be exactly 0.
Bottom line: it is true that GD might experience a little bump as it transitions through that cusp in the ReLU, but it’s not going to derail because of it. If you suspect that the cusp is getting in the way of your training, however, you can Google for variants of ReLU that replace the cusp with a smooth curve. There are at least two: the softplus and the Swish.
Sigmoid, ReLU, Leaky ReLU, softplus, Swish… You might feel a bit overwhelmed. Don’t we have a simple way to decide which of those functions to use in a neural network? Well, not quite—but we can take a look at a few pragmatic guidelines.
Picking the Right Function
When you design a neural network, you need to decide which activation functions to use. That decision usually boils down to a mix of experience and practical experimentation.
To begin with, however, you can follow a simple default strategy: just use ReLUs. They generally work okay, and they can help you deliver your first prototype as quickly as possible. Later on, you can experiment with other activation functions: Leaky ReLUs, maybe, or perhaps even sigmoids. Those other functions are likely to result in slower training than ReLUs, but they might improve the network’s accuracy.
This “ReLU as default” approach applies to all the layers in a network, except for the output layer. In general, the output layer in a classifier should use a softmax to output a probability-like number for each class.
You can make an exception to that rule if you only have two classes. In that case, you might want to use a sigmoid instead of a softmax in the last layer. To see why, consider a network that recognizes a vocal command. When you ask the system to classify a sound snippet, a softmax would output two numbers, like this:
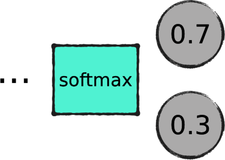
This result means “I’m 70% confident that I heard the command, and 30% confident that I didn’t.” In this case, however, the second output isn’t very useful because it always equals 1 minus the first output. For that reason, the softmax is overkill with only two classes, and you can replace it with a sigmoid:

To recap, here’s a no-nonsense default approach to picking activation functions: use ReLUs inside the network, and cap off the last layer with a softmax—or maybe a sigmoid, but only in the special case where you have two classes. This approach won’t always give you the best possible network, but it generally works fine as a starting point.
We took a long tour through activation functions, and we walked out with a few useful guidelines. Now let’s look at a few other techniques that can help you tame deep neural networks.