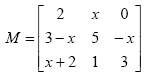8. Programming

In this chapter we introduce the basics of programming in MATLAB. The material presented in this chapter is not intended to be comprehensive or exhaustive but merely an introduction 23 to programming in MATLAB. In MATLAB programming, the list of commands and instructions are usually stored in a text file called an M-file (short for MATLAB file). These M-files can be of two kinds – either script files or function files. These files can be created or opened from the File menu by clicking on New or Open, then clicking on M-File. These files typically have the .m extension that is associated with MATLAB.

We will discuss script files first. The examples presented are simple. The reader can write more complicated examples based on the material presented here. Script files are used to store MATLAB scripts. A script is defined in MATLAB as a sequence of MATLAB commands. A script can span several lines. For example, here is a MATLAB script:

% This is an example
cost = 50
profit = 10
sale_price = cost + profit

Note that the first line in the script above is a comment line – this is optional. Store the above example in an M-file called example1.m then run the example by typing example1 at the command line to get:

>> example1

cost =

profit =

sale_price =

There are several remarks about the previous example. The first remark is that a script needs to be defined first (in an M-file) then executed by typing the name of the file (without the .m extension) on the command line. Note the use of the comment symbol % on the first line which is a comment line. The use of comments in scripts is optional but is useful to the reader. Note also that sometimes we do not need the results of all the commands displayed by MATLAB. For this purpose, we can use semicolons to suppress the outputs that are not needed. For example, here is the same example above with the output suppressed with semicolons except the last line:

% This is an example
cost = 50;
profit = 10;
sale_price = cost + profit

Store the above script in a new M-file and call it example2.m. Executing the above example by typing example2 at the command line will result in the following output:

>> example2

sale_price =

60

The second type of M-files in MATLAB is called a function file. These are more structured 24 than script files. In general, scripts are easier to write than functions but functions have their advantages. In fact, many of the commands used by MATLAB are stored in function files. Functions usually contain a sequence of MATLAB commands possibly spanning several lines. In addition, a function has a function name²⁵ and one or more arguments. In addition, a function returns a value²⁶. In contrast, a script does not have any arguments. For example, here is a function called area(r) that is stored in an M-File called area.m

function area(r)
% This is a function
area = pi*r^2

The above function calculates the area of a circle of radius r. The first line of the function file must have the word function followed by the name of the function and the argument(s) in parentheses. The last line of the function usually includes a calculation of the variable that is used for the name of the function. Now, run the above function by typing the name of the function followed by the argument in parentheses along with its value on the command line. Here is the result:

>> area(3)

area =

28.2743

A function may be executed several times with a different value for the argument each time. For example here is another execution of the previous function with the value 5 replacing 327:

>> area(5)

area =

78.5398

A function may be executed as many times as needed. However, it needs to be defined only once in an M-file. Here is an example of a function that calculates the perimeter of a rectangle with sides a and b:

function perimeter(a,b)
% This is another example of a function
perimeter = 2*(a+b)

It is clear that the above function has two arguments, namely a and b. Now, execute²⁸ the above function three times, each time for a certain rectangle with a specified length and width as follows:

>> perimeter(2,3)

perimeter =

>> perimeter(3,7)

perimeter =

>> perimeter(1.2,5.3)

perimeter =

It is clear that the first execution above calculates the perimeter for a rectangle with sides 2 and 3, the second execution calculates the perimeter with sides 3 and 7, while the third execution calculates the perimeter with sides 1.2 and 5.3 29.

Next, we will discuss briefly several constructs³⁰ that are used in programming in MATLAB - inside scripts and functions. In particular, we will discuss loops (the For loop and the While loop) and decisions (the If Elseif construct and the Switch Case construct).

In MATLAB loops, several command lines are executed repeatedly over many cycles depending on certain parameters in the loop. There are two types of loops in programming in MATLAB – the For loop and the While loop. Consider the following script file which is to be stored under the file name example3.m – this is an example of a For loop.

% This is an example of a FOR loop
for n = 1:10
x(n) = n^2;
end

Now, run the above script by typing the command example3 at the command prompt as follows:

>> example3

No output will be displayed because of the presence of the semicolon in the script file above. However, to find the value of the variable x, you need only to type x at the command prompt as follows:

> x

x =

1 4 9 16 25 36 49 64 81 100

It is seen from the above example that the For loop cycles over the values of n from 1 to 10 – exactly 10 times. In each cycle, the value of the vector x is calculated using the quadratic formula inside the For loop. The final result for the vector x is displayed above – it is seen that the vector x has exactly 10 elements.

Here is another example of a For loop to be stored in a script file called example4.m

%This is an example of another FOR loop
for n = 1:3
for m = 1:3
y(m,n) = m^2 + m*n + n^2;
end
end

Actually the above example contains two For loops that are nested. Now, run the above script file by typing example4 at the command prompt as follows, then type y to get the values of the elements of the matrix y:

>> example4
>> y

y =

3 7 13
7 12 19
13 19 27

It is seen that two nested For loops in this example can produce a matrix with a single assignment inside the For loops.

Another way to use loops in MATLAB is to use the While loop instead of the For loop. Here is an example of a While loop to be stored in a script file called example5.m

% This is an example of a While loop
tol = 0.0;
n = 0;
while tol < 10
n = n + 1;
tol = tol + 2;
end

Now, run the above example by typing example5 at the command prompt, then type tol and n to get their values after executing the script:

>> example5
>> n

n =

5

>> tol

tol =

It is seen from the above example that the loop will continue to cycle as long as the value of the variable tol is less than 31 10. As soon as the value of tol becomes equal to or larger than 10, the loop ends. The final values of the variables are then displayed by MATLAB with the appropriate commands. Note also the use of the semicolons in the script file.

Next, we discuss implementing decisions in programming in MATLAB. There are several constructs in MATLAB to use for decisions like the If construct, the If Else Then construct, the If Elseif Then construct, and the Switch Case construct. We will discuss these constructs briefly in the remaining part of this chapter.

Consider the following script file containing an If construct to be stored in a script file called example6.m

% This is an example using If Then
boxes = 10;
cost = boxes*3;
if boxes > 7
cost = boxes*2.5;
end

Now, run the above example by typing example6 at the command line. Then type the variable cost to see which answer we get as follows:

>> example6
>> cost

cost =

It is clear from the above example that we get 25 as the value of the variable cost. This is because the statement inside the If construct was executed. Actually, what happens is as follows: First, MATLAB computes the value of the variable cost as 30 using the first assignment statement for the variable cost. However, once we enter the If construct, the value of the variable cost may change depending on certain parameters. In this case, the value will change only if the value of the variable boxes is greater than 7. In our case, the value of the variable boxes is 10, so the effect of the If construct is to change the computation of the value of the variable cost from 30 to 25 using the second assignment statement for the variable cost – the one inside the If construct.

Here is the same example above but written as a function in a function file called cost.m. The function is called cost(boxes) and has one argument only. Writing the example as a function and not as a script will give us the option of changing the value of the variable boxes at the command prompt to see what effect it will have on the value of the variable cost. Here is the definition of the function:

function cost(boxes)
% This is an example of an If construct
cost = boxes*3
if boxes > 7
cost = boxes*2.5
end

Now, execute the above function using different values for the variable boxes. In this case, we will execute it three times to see the effect it has on the value of the variable cost as follows:

>> cost(4)

cost =

>> cost(6)

cost =

>> cost(8)

cost =

It is seen that the values of the variable cost for the first two executions were obtained directly using the first assignment statement for cost – this is because the value of the variable boxes is less than or equal to 7 in these two cases. However, for the third execution, the value of cost was calculated initially to be 24 but changed to 20 finally and correctly because the value of the variable boxes is larger than 7 in this last case.

Next, we discuss the If Elseif32 construct using a slightly modified version of the function cost(boxes). In this case, we call the function cost2(boxes) and define it as follows to be stored in a function file called cost2.m

function cost2(boxes)
% This is an example of an If Elseif construct
if boxes < 7
cost = boxes*2.5
elseif boxes < 9
cost = boxes*2
elseif boxes > 9
cost = boxes*1.5
end

Now, we execute the above function several times to test the results we get. We will execute it three times with the values of 6, 8, and 10 for the variable boxes. Here is what we get:

>> cost2(6)

cost =

15

>> cost2(8)

cost =

16

>> cost2(10)

cost =

15

In the above example, it is seen that the appropriate branch of the If Elseif construct and the appropriate assignment statement is used for the computation of the value of the variable cost depending on the value of the variable boxes. Note that several Elseif ‘s were needed to accomplish this. A more efficient way of doing this is to use the Switch Case construct. This is achieved by defining a new function cost3(boxes) to be stored in the function file cost3.m as follows (note that the functions cost2 and cost3 are not exactly equivalent):

function cost3(boxes)
% This is an example of the Switch Case construct
switch boxes
case 6
cost = boxes* 2.5
case 8
cost = boxes* 2
case 10
cost = boxes*1.5
otherwise
cost = 0
end

Now, execute the above function three times as before with the three values of 6, 8, and 10 for the variable boxes. This is what we get (exactly as before):

>> cost3(6)

cost =

15

>> cost3(8)

cost =

16

>> cost3(10)

cost =

15

Programming with the MATLAB Symbolic Math Toolbox

In this section we discuss scripts and functions using the MATLAB Symbolic Math Toolbox. Consider the following script where we square a symbolic matrix:

% This is an example with the Symbolic Math Toolbox
syms x
A = [x 1-x x+2 ; 2*x -3*x x ; 2-x 1-x x*2]
B = A^2

In the above script example, we define a symbolic variable x, then define the symbolic matrix A. Finally, we obtain the symbolic matrix B as the square of A. Now, store the above script in a script file called example7.m then run the script by typing example7 at the command prompt. This is what we get:

>> example7

A =

[   x, 1-x, x+2]
[ 2*x, -3*x,   x]
[ 2-x, 1-x, 2*x]

B =

[ x^2+2*(1-x)*x+(x+2)*(2-x), -2*(1-x)*x+(x+2)*(1-x), 3*x*(x+2)+(1-x)*x]
[ -4*x^2+x*(2-x), 3*(1-x)*x+9*x^2, 2*x*(x+2)-x^2]
[ 3*x*(2-x)+2*(1-x)*x, (2-x)*(1-x)-(1-x)*x, (x+2)*(2-x)+(1-x)*x+4*x^2]

Our next example will use a function file. Consider the following function SqureRoot(matrix) to be stored in a function file called SquareRoot.m

function SquareRoot(matrix)
% This is a function with Symbolic Variables
y = det(matrix)
z = subs(y,1)
if z < 1
M = 2*sqrt(matrix)
else
M = sqrt(matrix)
end

In the above function, the If Else construct is used to check the determinant of the matrix that is passed to the function. Once the determinant of the matrix is computed symbolically, we use the subs command to substitute the value of 1 for the symbolic variable x. If the value of the determinant of the matrix is less than 1, then we take twice the square root of the matrix (element-by element)33, otherwise, we take the square root of the matrix (element-by-element). Now, execute the above function with the following symbolic matrix to see the outcome:

>> syms x
>> M = [ 1-x x^2 ; x+3 x]

M =

[ 1-x, x^2]
[ x+3,   x]

>> SquareRoot(M)

y =

x-4*x^2-x^3

z =

-4

M =

[ 2*(1-x)^(1/2), 2*(x^2)^(1/2)]
[ 2*(x+3)^(1/2),     2*x^(1/2)]

In the next chapter, we will discuss graphs and plotting in MATLAB.

Exercises

Solve all the exercises using MATLAB. All the needed MATLAB commands for these exercises were presented in this chapter. Note that Exercises 10-11 require the use of the MATLAB Symbolic Math Toolbox.

Write a script of four lines as follows: the first line should be a comment line, the second and third lines should have the assignments cost = 200 and sale_price = 250, respectively. The fourth line should have the calculation profit = sale_price – cost. Store the script in a script file called example8.m. Finally run the script file.

Write a function of three lines to calculate the volume of a sphere of radius r. The first line should include the name of the function which is volume(r). The second line should be a comment line. The third line should include the calculation of the volume of the sphere which is .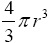
Store the function in a function file called volume.m then run the function with the value of r equal to 2 (no units are used in this exercise).

Write a function with two arguments to calculate the area of a rectangle with sides a and b. The function should have three lines. The first line should include the name of the function which is RectangleArea(a,b). The second line should be a comment line. The third line should include the calculation of the area of the rectangle with is the product a*b. Store the function in a function file called RectangleArea.m then run the function twice as follow: the first execution with the values 3 and 6, while the second execution with the values 2.5 and 5.5.

Write a script containing a For loop to compute the vector x to have the values x(n) = n³ where n has the range from 1 to 7. Include a comment line at the beginning. Store the script in a script file called example9.m then run the script and display the values of the elements of the vector x.

Write a script containing two nested For loops to compute the matrix y to have the values y(m,n) = m² – n² where both m and n each has the range from 1 to 4. Include a comment line at the beginning. Store the script in a script file called example10.m then run the script and display the values of the elements of the matrix y.

Write a script containing a While loop using the two variables tol and n. Before entering the While loop, initialize the two variables using the assignments tol = 0.0 and n = 3. Then use the two computations n = n + 1 and tol = tol + 0.1 inside the While loop. Make the loop end when the value of tol becomes equal or larger than 1.5. Include a comment line at the beginning. Store the script in a script file called example11.m then run the script and display the values of the two variables tol and n.

Write a function called price(items) containing an If construct as follows. Let the price of the items be determined by the computation price = items*130 unless the value of the variable items is greater than 5 – then in this case the computation price = items*160 should be used instead. Include a comment line at the beginning. Store the function in a function file called price.m then run the function twice with the values of 3 and 9 for the variable items. Make sure that the function displays the results for the variable price.

Write a function called price2(items) containing an If Elseif construct as follows. If the value of the variable items is less than 3, then compute the variable price2 by multiplying items by 130. In the second case, if the value of the variable items is less than 5, then compute the variable price2 by multiplying items by 160. In the last case, if the value of the variable items is larger than 5, then compute the variable price2 by multiplying the items by 200. Include a comment line at the beginning. Store the function in a function file called price2.m then run the function three times – with the values of 2, 4, and 6. Make sure that the function displays the results for the variable price2.

Write a function called price3(items) containing a Switch Case construct. The function should produce the same results obtained in Exercise 8 above. Include a comment line at the beginning. Store the function in a function file called price3.m then run the function three times – with the values of 2, 4, and 6. Make sure that the function displays the results for the variable price3.

Write a script file to store the following symbolic matrix A then calculate its third power B = A³ . Include a comment line at the beginning. Store the script in a script file called example12.m then run the script to display the two matrices A and B.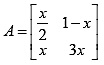

Write a function called SquareRoot2(matrix) similar to the function SquareRoot(matrix) described at the end of this chapter but with the following change. Substitute the value of 1.5 instead of 1 for the symbolic variable x. Make sure that you include a comment line at the beginning. Store the function in a function file called SquareRoot2.m then run the function using the following symbolic matrix: