2. Arithmetic Operations
In this chapter we learn how to perform the simple arithmetic operations of addition, subtraction, multiplication, division, and exponentiation. The first four operations of addition, subtraction, multiplication, and division are performed in MATLAB using the usual symbols +, -, *, and /. The following are some examples:
In the next chapter, we will show how to control the number of decimal digits that appear in the answer. The operation of exponentiation is performed using the symbol ^ as shown in the following examples:
>> 2^3
ans =
8
>> 2^-3
ans =
0.1250
>>
>> -2^3
ans =
-8
>> -2^4
ans =
-16
>> (-2)^4
ans =
16
In the above examples, be careful where the minus sign is used. The constants π and ε are obtained in MATLAB as follows:
>> pi
ans =
3.1416
>> eps
ans =
2.2204e-016
In the above examples, the constant π is denoted by the command pi and represents the ratio of the perimeter of a circle to its diameter. The other constant ε is denoted by the command eps and represents the smallest number that MATLAB can handle.
In the above examples, only one arithmetic operation was performed in each line. Alternatively, we can perform multiple arithmetic operations in each line or command. The following are some examples:
In these cases, the order of operations is very important because the final computed result depends on this order. Precedence of computation is for the exponentiation operation, followed by multiplication and division, then followed by addition and subtraction. For example, in the examples above, multiplication is performed before addition and division is performed before addition. In case you need to perform addition before multiplication or division, the above two examples may be computed using parentheses as follows:
>> 3*(4+5)
ans =
27
>> (2+5)/4
ans =
1.7500
It is clear from the above examples that the operations inside the parentheses take precedence over any other operations. Several multiple operations may also be performed as follows:
One should be careful when using parentheses. A change of the position of the parenthesis in the above example will change the computed results as follows:
>> (26+53)-(3^4 +5*2)/3
ans =
48.6667
Arithmetic Operations with the MATLAB Symbolic Math Toolbox
Symbolic arithmetic operations may also be performed in MATLAB using the MATLAB Symbolic Math Toolbox. For the next examples, this toolbox needs to be installed with MATLAB. In order to perform symbolic operations in MATLAB, we need to define symbolic numbers3 using the sym command. For example, ½ is defined as a symbolic number as follows:
>> sym(1/2)
ans =
1/2
In the above example, the number ½ is stored in MATLAB without any approximation using decimal digits like 0.5. Once used with the sym command, the computations will be performed algebraically or symbolically. For example, the following addition of two fractions is performed numerically as follows without the sym command:
Adding parentheses will not affect the numerical computation in this case:
>> (1/2)+(3/5)
ans =
1.1000
However, using the sym command of the MATLAB Symbolic Math Toolbox will result in the computation performed symbolically without the use of decimal digits;
>> sym((1/2)+(3/5))
ans =
11/10
Notice in the above example how the final answer was cast in the form of a fraction without decimal digits and without calculating a numerical value. In the addition of the two fractions above, MATLAB finds their common denominator and adds them by the usual procedure for rational numbers. Notice also in the above four example outputs that symbolic answers are not indented but numerical answers are indented. In the next chapter, we will study variables and their use in MATLAB.
Solve all the exercises using MATLAB. All the needed MATLAB commands for these exercises were presented in this chapter. Note that Exercises 19 and 21 require the use of the MATLAB Symbolic Math Toolbox.
- Perform the addition operation 7+9.
- Perform the subtraction operation 16-10.
- Perform the multiplication operation 2*9.
- Perform the division operation 12/3.
- Perform the division operation 12/5.
- Perform the exponentiation operation 3^5.
- Perform the exponentiation operation 3*(-5).
- Perform the exponentiation operation (-3)^5.
- Perform the exponentiation operation -3^5.
- Compute the value of
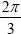 .
. - Obtain the value of the smallest number that can be handled by MATLAB.
- Perform the multiple operations 5+7-15.
- Perform the multiple operations (6*7)+4.
- Perform the multiple operations 6*(7+4).
- Perform the multiple operations 4.5 + (15/2).
- Perform the multiple operations (4.5 + 15)/2.
- Perform the multiple operations (15 – 4 + 12)/5 – 2*(7^4)/100.
- Perform the multiple operations (15 – 4) + 12/5 – (2*7)^4/100.
- Define the number 2/3 as a symbolic number.
- Perform the fraction addition (2/3) + (3/4) numerically.
- Perform the fraction addition (2/3) + (3/4) symbolically.