3. Variables

In this chapter we introduce variables and how to deal with them in MATLAB. If you do not use a variable, then MATLAB automatically stores the calculated result in the variable ans. The following is an example:

>> 3+2

ans =

5

In the above example, the number 5 is stored automatically in the variable ans. This variable is short for “answer”. If you wish to store the number 5 in another variable, then you need to specify it as follow:

>> x=3+2

x =

5

In the above example, we used the variable x to store the result which is 5. You may define the variables x, y, z as follows without performing any operations:

>> x=1

x =

1

>> y=-3

y =

-3

>> z=3.52

z =

3.5200

Note that MATLAB is case-sensitive with respect to variables. For example, the variables x and X are different. The following example illustrates this issue:

>> x=5

x =

5

>> X=3

X =

3

>> x

x =

5

>> X

X =

3

We may perform arithmetic operations on variables as shown in the following examples:

>> x=4

x =

4

>> y=2.5

y =

2.5000

>> z=x+y

z =

6.5000

>> w=2*x-3*z+y

w =

-9

Up till now, we have used single letters to denote variables. Any string of characters may be used to denote variables also. For example, we next use the variables result and the_answer_is as follows:

>> a=3

a =

3

>> b=-2

b =

-2

>> result = a*b
result =

-6

>> the_answer_is = 2*a/b

the_answer_is =

-3

Since MATLAB is case-sensitive, then the variables width, WIDTH, and Width are all different and store different results. You may add comments to your MATLAB commands and statements by using the symbol %. Comments are not executed and are ignored by MATLAB but are included for the benefit of the reader. For example, here is a comment:

>> % This is a comment

Comments are displayed in green color on the MATLAB screen. You may also add a comment on the same line as a command. The following is an example:

>> x = 6 % the value of x is defined here

x =

6

The following are the MATLAB rules for naming variables:

MATLAB is case-sensitive with respect to variables.
All variables must start with a letter.
You may have up to 31 characters in a variable.
Punctuation signs are not allowed in a variable.
The underscore sign “_” is allowed in a variable.
Both letters and digits are allowed in a variable.

For example, we may define variables x1, x2, and x3 as follows:

>> x1 = 1

x1 =

1

>> x2 = -2.7

x2 =

-2.7000

>> x3 = 2*x1/x2

x3 =

-0.7407

All variable used must be defined. For example, we get an error if we try to use a variable that is not defined. For example, the variable h is not defined as follows:

>> 3*h/2
??? Undefined function or variable 'h'.

The error is displayed in red color on the MATLAB screen. To find all the variables used in a MATLAB session, use the who command as follows:

>> who

Your variables are:

X result x1 z
a the_answer_is x2
ans w x3
b x y

The who command does not provide any details about the variables. The following is an example on using variables. If you know the cost and sale price of an item, calculate the profit. Here is the example:

>> cost = 100

cost =

100

>> sale_price = 120

sale_price =

120

>> profit = sale_price - cost

profit =

20

Numbers in MATLAB are displayed with four decimal digits by default. For example:

>> 7/3

ans =

2.3333

However, MATLAB performs the calculations internally using about 16 digits. You may ask MATLAB to display results with 16 digits using the command format long as follows:

>> format long
>> 7/3

ans =

2.33333333333333

>> format short
>> 7/3

ans =

2.3333

The command format short tells MATLAB to display four decimals again. Finally, you may ask MATLAB to show all variables used in a session with details regarding size, bytes 4, and class⁵ using the whos command as follows:

>> whos

See Table

To clear all the variables in a session, use the clear command as follows:

>> clear

After you use the clear command, the command who or whos will not display any variables. Here is another example. If you know the radius of a circle, then calculate both the perimeter and area of the circle. The solution is:

radius =

12.3000

>> perimeter = 2*pi*radius

perimeter =

77.2832

>> area = pi*radius^2

area =

475.2916

In the above example, we have used the constant pi that was defined in Chapter 2. Also, note the use of the two arithmetic operations of multiplication and exponentiation.

Variables with the MATLAB Symbolic Math Toolbox

You may also use symbolic variables 6 in MATLAB. For example, the variables x and y are defined as symbolic variables as follows:

>> x=1/2

x =

0.5000

>> y= 2/3

y =

0.6667

>> sym(x)

ans =

1/2

>> sym(y)

ans =

2/3

Arithmetic operations can now be performed on these symbolic variables. Consider the following example where the variables x and y were defined as above :

>> z=sym(x-y)

z =

-1/6

In the above example, the variable z is used automatically as a symbolic variable. For symbolic operations, the important thing is to start each operation or calculation with the sym command. Here is another example to calculate the volume of a sphere:

>> r=15/7

r =

2.1429

>> sym(r)

ans =

15/7

>> volume = sym(4*pi*r^3/3)

volume =

4500*pi/343

In the above example, the final answer is given in the form of a fraction, 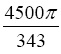, with no decimal expressions and without calculating a numerical value (no units are used in this example). In case you need to have this value calculated numerically, then you can need to use the double command as follows:

>> double(volume)

ans =

41.2162

It is seen thus that the value of the volume of the sphere is 41.2162 (no units are used in this example). Finally, the variables x and this can be defined as symbolic variables without assigning a numerical value as follows:

>> x = sym('x')

x =

x

>> this = sym('this')

this =

this

In the next chapter, we will study mathematical functions and their use with variables.

Exercises

Solve all the exercises using MATLAB. All the needed MATLAB commands for these exercises were presented in this chapter. Note that Exercises 21-27 require the use of the MATLAB Symbolic Math Toolbox.

Perform the operation 2*3+7 and store the result in the variable w.

Define the three variables a, b, and c equal to 4, -10, and 3.2, respectively.

Define the two variables y and Y equal to 10 and 100. Are the two variables identical?

Let x = 5.5 and y = -2.6. Calculate the value of the variable z = 2x-3y.

In Exercise 4 above, calculate the value of the variable w = 3y – z + x/y.

Let r = 6.3 and s = 5.8. Calculate the value of the variable final defined by final = r + s - r*s.