5. Complex Numbers

In this chapter we discuss complex numbers and how to deal with them in MATLAB. A complex number has two parts – one real part and one imaginary part. The imaginary part of a complex number is usually the square root of a negative real number. The simplest complex number is the square root of -1 which is obtained in MATLAB as follows:

>> sqrt(-1)

ans =

    0 + 1.0000i

The imaginary part of a complex number is usually denoted by the symbol i where 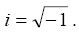image In this case the real part is zero. Some people prefer to use the symbol j instead of i to denote imaginary parts of complex numbers. Here is an example of a complex number:

>> 3+sqrt(-7)

ans =

  3.0000 + 2.6458i

In the above example, the real part is 3.0 and the imaginary part is 2.6458. We can also use variables with complex numbers. Define the variables a and b as complex numbers as follows:

>> a = 3+2i

a =

 3.0000 + 2.0000i

>> b = 5-4i

b =

 5.0000 - 4.0000i

Arithmetic operations can also be performed on complex numbers. For example, addition, subtraction, multiplication, and division can be performed on the variables a and b as follows:

>> a+b

ans =

 8.0000 - 2.0000i

>> a-b

ans =

 -2.0000 + 6.0000i

>> a*b

ans =

 23.0000 - 2.0000i

>> a/b

ans =

 0.1707 + 0.5366i

Exponentiation can also be performed on the complex numbers a and b as follows:

>> a^3

ans =

 -9.0000 +46.0000i

>> b^(-2)

ans =

  0.0054 + 0.0238i

Multiple arithmetic operations can also be performed on the complex numbers a and b as follows (the result is always a complex number):

>> 2*a + 3*b -5

ans =

 16.0000 - 8.0000i

>> a - i*b*4

ans =

  -13.0000 -18.0000i

There are some mathematical functions that can be used with complex numbers. For example, the MATLAB commands abs and angle can be used to obtain the magnitude and angle of a complex number, respectively. Here is an example of how to use these two commands:

>> abs(2+3i)

ans =

 3.6056

>> angle(2+3i)

ans =

 0.9828

In the above example, the angle of the complex number is obtained in radians. If you need the angle in degrees, then you have to multiply the result by 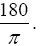image Here is an example:

>> angle(2+3i)*180/pi

ans =

 56.3099

The real and imaginary parts of a complex number can be extracted using the MATLAB commands real and imag as follows:

>> real(2+3i)

ans =

 2

>> imag(2+3i)

ans =

  3

The complex conjugate of a complex number can be obtained using the MATLAB command conj as follows:

>> conj(2+3i)

ans =

 2.0000 - 3.0000i

A new complex number may be formed from real and imaginary parts using the MATLAB command complex as follows:

>> complex(2,3)

ans =

 2.0000 + 3.0000i

Trigonometric functions can also be used with complex numbers. Here are some examples:

>> sin(2+3i)

ans =

 9.1545 - 4.1689i

>> cos(2+3i)

ans =

 -4.1896 - 9.1092i

>> tan(2+3i)

ans =

 -0.0038 + 1.0032i

In the above examples, the result is always a complex number. Exponential and logarithmic functions can also be used with complex numbers. Here are two examples:

>> exp(2+3i)

ans =

 -7.3151 + 1.0427i

>> log(2+3i)

ans =

 1.2825 + 0.9828i

In the above example, we have computed e2+3i and ln(2 + 3i) , respectively. Finally, here are some examples for computing the quantities sin(2π i) , cos(2π i) , and e2π i :

>> sin(2*pi*i)

ans =

   0 +2.6774e+002i

>> cos(2*pi*i)

ans =

 267.7468

>> exp(2*pi*i)

ans =

 1.0 - 0.0000i

From the last example above, we note that the result of e2π i is the real number 1. We can also raise quantities to a complex number. Here is an example:

>> (2+3i)^(1-5i)

ans =

 3.2272e+002 +3.7004e+002i

As can be seen above, the result is usually a complex number.


Complex Numbers with the MATLAB Symbolic Math Toolbox


The MATLAB Symbolic Math Toolbox can also be used with complex numbers. For example, we define 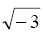imageusing the sym command as follows:

>> sym(sqrt(-3))

ans =

(0)+(sqrt(3))*i

The magnitude and angle of a complex number may be obtained symbolically using the abs and angle commands along with the sym command as follows:

>> sym(abs(2+3i))

ans =

sqrt(13)

>> sym(angle(2+3i))

ans =

8852218891597467*2^(-53)

>> double(ans)

ans =

  0.9828

In the above example, we used the double command to obtain the angle numerically in radians. Trigonometric functions can also be used with the sym command along with complex numbers but the double command may need to be used to obtain the final result numerically. Here is an example:

>> sym(sin(2+3i))

ans =

(5153524868349230*2^(-49))-(4693771957861922*2^(-50))*i

>> double(ans)

ans =

 9.1545 - 4.1689i

The same remark above applies also to the exponential, logarithmic, and other mathematical functions in MATLAB. In the next chapter, we introduce vectors and their use in MATLAB.


Exercises


Solve all the exercises using MATLAB. All the needed MATLAB commands for these exercises were presented in this chapter. Note that Exercises 18-21 require the use of the MATLAB Symbolic Math Toolbox.


  1. Compute the square root of -5.
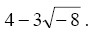
  2. Define the complex number image
  3. Define the two complex numbers with variables x and y where x = 2 − 6i and y = 4 + 11i .
  4. In Exercise 3 above, perform the addition and subtraction operations x + y and x − y.
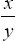  5. In Exercise 3 above, perform the multiplication and division operations x y and image.
  6. In Exercise 3 above, perform the exponentiation operations x4 and y−3.
  7. In Exercise 3 above, perform the multiple operations 4x − 3y + 9.
  8. In Exercise 3 above, perform the multiple operations ix − 2y − 1.
  9. Compute the magnitude of the complex number 3 − 5i.
  10. Compute the angle of the complex number 3 − 5i in radians.
  11. Compute the angle of the complex number 3 − 5i in degrees.
  12. Extract the real and imaginary parts of the complex number 3 − 5i.
  13. Obtain the complex conjugate of the complex number 3 − 5i.
  14. Compute the sine, cosine, and tangent functions of the complex number 3 − 5i.
  15. Compute e3−5i and ln(3 − 5i).
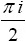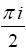  16. Compute the values of sin image , cos image and eπ i / 2.
  17. Compute the value of (3 + 4i)(2−i).
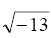  18. Obtain image symbolically.
  19. Obtain the magnitude of the complex number 3 − 5i symbolically.
  20. Obtain the angle of the complex number 3 − 5i symbolically. Make sure that you use the double command at the end.
  21. Obtain the cosine function of the complex number 3 − 5i symbolically. Make sure that you use the double command at the end.