6. Vectors
In this chapter we introduce vectors9 and how to deal with them in MATLAB. Vectors are stored in MATLAB as one-dimensional arrays. For example, here is a vector stored in the variable x:
>> x = [ 1 3 0 5 -2 ]
x =
1 3 0 5 -2
In the above example, the vector x contains five elements. It is noticed that the elements of a vector in MATLAB are separated by spaces and enclosed between brackets. To extract the second element of the vector x, we use the notation x(2) as follows:
>> x(2)
ans =
3
Here is another example where we extract the fifth element of the vector x:
>> x(5)
ans =
-2
Here is a vector y defined implicitly with five elements as follows:
>> y = pi*x
y =
3.1416 9.4248 0 15.7080 -6.2832
In the above example, the vector y is obtained from the vector x by multiplying each element of the vector x by π. To extract the fourth element of the vector y, we use the notation y(4) as follows:
>> y(4)
ans =
15.7080
As we have seen above, we use the notation y(n) where y is the variable where the vector is stored and n is an integer ranging from 1 to the length of the vector. We have to be careful when we use this notation – n has to be an integer. If we try to use y(1.2) then we obtain an error message as follows (because 1.2 is not an integer):
>> y(1.2)
??? Subscript indices must either be real positive integers or logicals.
In order to extract the first three elements of the vector y, we use the notation y(1:3) as follows:
The length of a vector is the number of elements contained in the vector. In order to obtain the length of a vector, we use the MATLAB command length as follows:
>> length(y)
ans =
5
In order to add the total sum of the values of the elements of a vector, we use the MATLAB command sum as follows:
>> sum(y)
ans =
21.9911
In order to find the minimum value and the maximum value of the elements of a vector, we use the MATLAB commands min and max, respectively, as follows:
>> min(y)
ans =
-6.2832
>> max(y)
ans =
15.7080
In the above examples of vectors, we constructed the vectors by listing their elements either explicitly or implicitly. There are two other ways to construct vectors in MATLAB. For example, the vector a is constructed (using parentheses) as follows:
>> a = (0:0.2:1)
a =
0 0.2000 0.4000 0.6000 0.8000 1.0000
In the above example, the vector a contains all the real numbers between 0 and 1 with an increment of 0.2. Another way to construct vectors in MATLAB is to use the linspace10 command (using parentheses) as follows:
>> b = linspace(0,5,10)
b =
Columns 1 through 6
0 0.5556 1.1111 1.6667 2.2222 2.7778
Columns 7 through 10
3.3333 3.8889 4.4444 5.0000
In the above example, the vector b is constructed such that it contains 10 elements between 0 and 5 that are equally spaced11. Ignore the MATLAB output where it says “Columns ? to ?” – this notation will become clear to us when we study matrices in the next chapter.
Two vectors can be joined together to form a new vector. In the following example, the two vectors a and b are joined together to form the new vector c:
>> a = [ 1 3 5]
a =
1 3 5
>> b = [ 7 9 ]
b =
7 9
>> c = [a b]
c =
1 3 5 7 9
Based on the above example, we can also form a new vector d as follows:
>> d = [a b 11]
d =
1 3 5 7 9 11
Next, we will discuss the arithmetic operations that are allowed with vectors. The operations of addition and subtraction can be performed on two vectors of the same length. Here is an example:
>> x = [0.1 0.3 -2 5]
x =
0.1000 0.3000 -2.0000 5.0000
>> y = [0.25 0.4 1 0]
y =
0.2500 0.4000 1.0000 0
>> x+y
ans =
0.3500 0.7000 -1.0000 5.0000
>> x-y
ans =
-0.1500 -0.1000 -3.0000 5.0000
If you try to add or subtract two vectors of different lengths, then you will get an error message. Here is an example:
>> a = [1 5 3 5 6]
a =
1 5 3 5 6
>> b = [-2 3 5 7]
b =
-2 3 5 7
>> a+b
??? Error using ==> plus
Matrix dimensions must agree.
>> a-b
??? Error using ==> minus
Matrix dimensions must agree.
The operation of multiplication is a little more complicated for vectors. Even if you try to multiply two vectors of the same length, you will get an error message. Here is an example using the vectors x and y of the same length defined above:
>> x*y
??? Error using ==> mtimes
Inner matrix dimensions must agree.
Note that the operation of division is absolutely not defined for vectors – you cannot divide one vector by another. However, you can perform the new operations of element-by-element multiplication and element-by-element division of vectors in MATLAB using the vectors x and y defined above as follows:
>> x.*y
ans =
0.0250 0.1200 -2.0000 0
>> x./y
Warning: Divide by zero.
ans =
0.4000 0.7500 -2.0000 Inf
Note in the above example that the symbols for multiplication and division are preceded by a dot. The dot tells MATLAB to perform the operations element by element. Note that in order to carry these element-by-element operations, the two vectors must be of the same length.
There is another type of multiplication that is defined for vectors. It is called the scalar product, the inner product, or the dot product12 – three different names for the same operation. This product is obtained in MATLAB for the two vectors x and y defined above as follows:
>> x*y'
ans =
-1.8550
The final outcome of this operation is always a scalar or a number – not a vector. In addition, the two vectors that are used must be of the same length. Note the use of the prime on the second vector in the operation above. The use of the prime indicates the transpose operation which we will discussed in detail in the next chapter on matrices.
There are other simpler operations that can be performed on vectors. The operations of scalar addition and scalar subtraction can be performed as in the following example:
In the above example, the number 4 is added to each element of the vector while the number 3 is subtracted from each element of the vector. In addition, the operations of scalar multiplication and scalar division can also be performed on the vector s defined above as follows:
>> s*2
ans =
2 8 -6 4 4
>> s/5
ans =
0.2000 0.8000 -0.6000 0.4000 0.4000
In the first example above, each element of the vector s is multiplied by the number 2 while in the second example, each element of the vector s is divided by the number 5. The above four operations can also be combined together using the vector s defined above as follows:
>> 2+ s/2.4
ans =
2.4167 3.6667 0.7500 2.8333 2.8333
Mathematical functions can also be used with vectors. Here is an example where we use the three trigonometric functions on the vector a defined below:
>> a = [0 pi/2 pi 3*pi/2 2*pi]
a =
0 1.5708 3.1416 4.7124 6.2832
>> sin(a)
ans =
0 1.0000 0.0000 -1.0000 -0.0000
>> cos(a)
ans =
1.0000 0.0000 -1.0000 -0.0000 1.0000
>> tan(a)
ans =
1.0e+016 *
0 1.6331 -0.0000 0.5444 -0.0000
In the above example, the trigonometric operations are carried out element-by-element. Here is an example with the same vector a where we use the exponential function:
>> exp(a)
ans =
1.0000 4.8105 23.1407 111.3178 535.4917
In the above example, the exponential function is carried out element-by-element. Here is another example where we use the square root functions on the vector a defined above as follows:
>> sqrt(a)
ans =
0 1.2533 1.7725 2.1708 2.5066
Note that the square root operation was performed element by element in the example above. The last operation that we will discuss is the exponentiation operation. If we try to evaluate the quantity 2a where a is the vector defined above, then we will receive an error message as follows:
In order to carry out the exponentiation operation element by element, we need to include the dot symbol before the exponentiation symbol as follows:
>> 2.^a
ans =
1.0000 2.9707 8.8250 26.2162 77.8802
In the above example, the exponentiation operation is carried out element by element.
There are certain types of vectors that can be generated automatically by MATLAB. These types of vectors have specific commands for their generation. For example, the MATLAB commands ones and zeros produce vectors with elements of 1’s and 0’s, respectively. Here are two examples:
>> t = ones(1,7)
t =
1 1 1 1 1 1 1
>> w = zeros(1,5)
w =
0 0 0 0 0
The exact use of the above two commands will be discussed in detail in the next chapter on matrices. Elements of a vector can be sorted using the MATLAB command sort as follows:
>> x = [2 1 -3 5 3]
x =
2 1 -3 5 3
>> sort(x)
ans =
-3 1 2 3 5
Sorting in the above example has been obtained in an ascending order13. Finally, a vector with its element forming a random permutation can be generated using the randperm command as follows:
>> randperm(7)
ans =
2 7 4 3 6 5 1
In the above example, a random permutation of seven elements is obtained.
There are some MATLAB commands for statistics that can be used with vectors. For example, the MATLAB commands range, mean, and median can be used to obtain the statistical values of range, mean, and median for a set of numbers in a vector as follows:
>> w = [1 5 -2 0 4 6]
w =
1 5 -2 0 4 6
>> range(w)
ans =
8
>> mean(w)
ans =
2.3333
>> median(w)
ans =
2.5000
Vectors with the MATLAB Symbolic Math Toolbox
In this section, we will discuss the use of symbolic vectors in MATLAB. Symbolic vectors are vectors whose elements are handled algebraically without numerical computations. In the following example, we define a symbolic vector a of three elements using the MATLAB command syms:
Next, we carry out the following scalar addition operation on the vector a defined previously to obtain the new symbolic vector b:
>> b = 2+a
b =
[ x+2, y+2, z+2]
Next, we extract the second element of the vector b as follows:
>> b(2)
ans =
y+2
Next, we perform the addition of the two vectors a and b to get the new symbolic vector c as follows:
>> c = a+b
c =
[ 2*x+2, 2*y+2, 2*z+2]
Next, we perform the operation 2*a – 3*b/5 to obtain the new symbolic vector d as follows:
Next, we obtain the dot product of the vector a and b as follows:
>> a*b'
ans =
x*(2+conj(x))+y*(2+conj(y))+z*(2+conj(z))
In the above example, notice that the result is a scalar quantity (a symbolic or algebraic expression) – not a vector. We can also perform the dot product in the following way by reversing the order of the two vectors:
>> b*a'
ans =
(x+2)*conj(x)+(y+2)*conj(y)+(z+2)*conj(z)
Notice that the two dot products obtained above are different. They would be exactly the same if the variables x, y, and z were real variables. MATLAB assumes by default that these are complex variables thus obtaining two different results.
Next, we obtain the square root of the vector a-b element by element as follows:
The symbolic vector obtained above is a complex vector, i.e. a vector with complex elements. Finally, we can obtain a numerical value for the above expression by using the MATLAB command double as follows:
>> double(ans)
ans =
0 + 1.4142i 0 + 1.4142i 0 + 1.4142i
It is clear from the above result that the final vector is a complex vector with its elements being complex numbers. In the next chapter we will discuss the use of matrices in MATLAB.
Exercises
Solve all the exercises using MATLAB. All the needed MATLAB commands for these exercises were presented in this chapter. Note that Exercises 36-41 require the use of the MATLAB Symbolic Math Toolbox.
- Store the vector [2 4 -6 0] in the variable
w. - In Exercise 1 above, extract the second element of the vector
w. - In Exercise 1 above, generate the vector
zwhere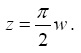
- In Exercise 3 above, extract the fourth element of the vector
z. - In Exercise 3 above, extract the first three elements of the vector
z. - In Exercise 3 above, find the length of the vector
z. - In Exercise 3 above, find the total sum of the values of the elements of the vector
z. - In Exercise 3 above, find the minimum and maximum values of the elements of the vector
z. - Generate a vector
rwith real values between 1 and 10 with an increment of 2.5. - Generate a vector
swith real values of ten numbers that are equally spaced between 1 and 100. - Form a new vector by joining the two vectors [9 3 -2 5 0] and [1 2 -4].
- Form a new vector by joining the vector [9 3 -2 5 0] with the number 4.
- Add the two vectors [0.2 1.3 -3.5] and [0.5 -2.5 1.0].
- Subtract the two vectors in Exercise 13 above.
- Try to multiply the two vectors in Exercise 13 above. Do you get an error message? Why?
- Multiply the two elements in Exercise 13 above element by element.
- Divide the two elements in Exercise 13 above element by element.
- Find the dot product of the two vectors in Exercise 13 above.
- Try to add the two vectors [1 3 5] and [3 6]. Do you get an error message? Why?
- Try to subtract the two vectors in Exercise 20 above. Do you get an error message? Why?
- Let the vector w be defined by
w= [0.1 1.3 -2.4]. Perform the operation of scalar addition5+w. - In Exercise 22 above, perform the operation of scalar subtraction
-2-w. - In Exercise 22 above, perform the operation of scalar multiplication
1.5*w. - In Exercise 22 above, perform the operation of scalar division
w/10. - In Exercise 22 above, perform the operation
3 – 2*w/5. - Define the vector
bbyb= [0 pi/3 2pi/3 pi]. Evaluate the three vectors sin b , cosb , and tan b (element by element). - In Exercise 26 above, evaluate the vector eb (element by element).
- In Exercise 26 above, evaluate the vector
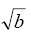 (element by element).
(element by element). - Try to evaluate the vector 3b. Do you get an error message? Why?
- Perform the operation in Exercise 29 above element by element?
- Generate a vector of 1’s with a length of 4 elements.
- Generate a vector of 0’s with a length of 6 elements.
- Sort the elements of the vector [0.35 -1.0 0.24 1.30 -0.03] in ascending order.
- Generate a random permutation vector with 5 elements.
- For the vector [2 4 -3 0 1 5 7], determine the range, mean, and median.
- Define the symbolic vector
x= [r s t u v]. - In Exercise 36 above, perform the addition operation of the two vectors
xand [1 0 -2 3 5] to obtain the new symbolic vectory. - In Exercise 37 above, extract the third element of the vector
y. - In Exercise 37 above, perform the operation
2*x/7 + 3*y. - In Exercise 37 above, perform the dot products
x*y’andy*x’. Are the two results the same? Why? - In Exercise 37 above, find the square root of the symbolic vector
x+y.