© Springer Nature Switzerland AG 2019
M. Weiland et al. (eds.)High Performance ComputingLecture Notes in Computer Science11887https://doi.org/10.1007/978-3-030-34356-9_44

Acceleration of Scientific Deep Learning Models on Heterogeneous Computing Platform with Intel® FPGAs

Chao Jiang1  , Dave Ojika1  , Thorsten Kurth2  , Prabhat2  , Sofia Vallecorsa3  , Bhavesh Patel4   and Herman Lam1  
(1)
SHREC: NSF Center for Space, High-Performance and Resilient Computing, Gainesville, USA
(2)
National Energy Research Scientific Computing Center (NERSC), Berkeley, USA
(3)
CERN openlab, Geneva, Switzerland
(4)
Dell EMC, Hopkinton, USA
 
 
Chao Jiang (Corresponding author)
Email: jc19chaoj@ufl.edu
 
Dave Ojika
Email: davido@ufl.edu
 
Thorsten Kurth
Email: tkurth@lbl.gov
 
Prabhat
Email: prabhat@lbl.gov
 
Sofia Vallecorsa
Email: sofia.vallecorsa@cern.ch
 
Bhavesh Patel
Email: bhavesh.a.patel@dell.com
 
Herman Lam
Email: hlam@ufl.edu

Abstract

AI and deep learning are experiencing explosive growth in almost every domain involving analysis of big data. Deep learning using Deep Neural Networks (DNNs) has shown great promise for such scientific data analysis applications. However, traditional CPU-based sequential computing can no longer meet the requirements of mission-critical applications, which are compute-intensive and require low latency and high throughput. Heterogeneous computing (HGC), with CPUs integrated with accelerators such as GPUs and FPGAs, offers unique capabilities to accelerate DNNs. Collaborating researchers at SHREC$$^{1}$$ at the University of Florida, NERSC$$^{2}$$ at Lawrence Berkeley National Lab, CERN Openlab, Dell EMC, and Intel are studying the application of heterogeneous computing (HGC) to scientific problems using DNN models. This paper focuses on the use of FPGAs to accelerate the inferencing stage of the HGC workflow. We present case studies and results in inferencing state-of-the-art DNN models for scientific data analysis, using Intel distribution of OpenVINO, running on an Intel Programmable Acceleration Card (PAC) equipped with an Arria 10 GX FPGA. Using the Intel Deep Learning Acceleration (DLA) development suite to optimize existing FPGA primitives and develop new ones, we were able accelerate the scientific DNN models under study with a speedup from 3$$\times $$ to 6$$\times $$ for a single Arria 10 FPGA against a single core (single thread) of a server-class Skylake CPU.

1 Introduction

AI and deep learning are experiencing explosive growth in almost every domain involving analysis of big data. Deep learning(DL) using Deep Neural Networks (DNNs) has shown great promise for such scientific data analysis applications. However, traditional CPU-based sequential computing without special instructions can no longer meet the requirements of mission-critical applications, which are compute-intensive and require low latency and high throughput. Heterogeneous computing (HGC), using CPUs integrated with accelerators such as GPUs and FPGAs, offers unique capabilities to accelerate DNNs. At the University of Florida site of the NSF Center for Space, High-Performance, and Resilient Computing (SHREC: www.​nsf-shrec.​org), we are developing such an HGC system to support a complete HGC workflow for deep learning. This project is a collaborative effort between SHREC and NERSC at Berkeley National Lab, CERN openlab, Dell EMC, and Intel.
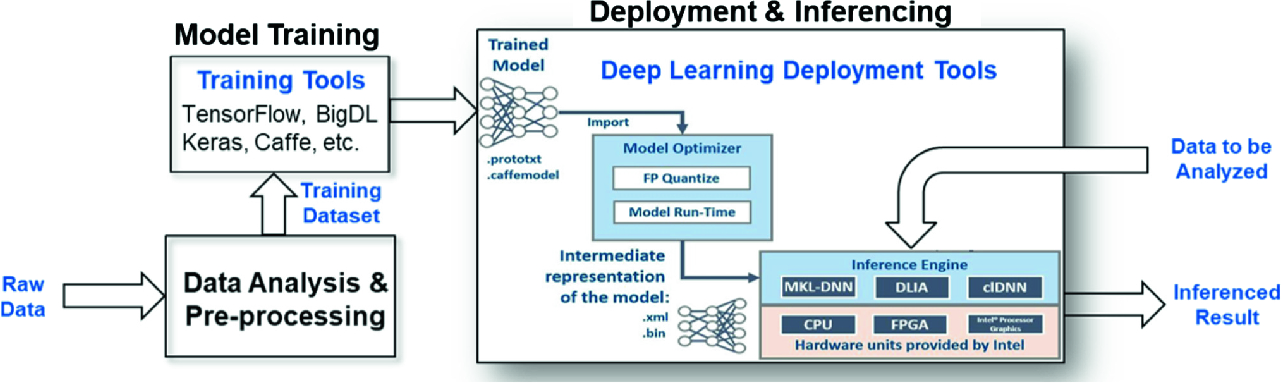
../images/491247_1_En_44_Chapter/491247_1_En_44_Fig1_HTML.png
Fig. 1.

Heterogeneous computing workflow for machine learning

The concept diagram for the HGC workflow for deep learning is shown in Fig. 1. The HGC workflow consists of three stages:
  1. 1.

    Data Analysis and Pre-processing

     
  2. 2.

    Model Training

     
  3. 3.

    Deployment and Inferencing

     

The Data Analysis and Pre-processing stage converts raw data from an application of interest into a form that is suitable for model training using any of the training frameworks. Current pre-processing methods include data cleaning, data normalization, and data augmentation [13]. In the HGC workflow, the pre-processed data is used as inputs to the training tools in the Model Training stage. Currently, popular open-source frameworks for training these models include TensorFlow [2], Keras [5], Caffe [17], and BigDL [6]. The output of the Training stage is trained models which are used in inference engines in the Deployment and Inferencing stage. Some of the common approaches for running inferencing primarily use Xeon CPU; but recently there has been much interest in using FPGAs (field programmable gate arrays) for inferencing. This paper will focus on how we can use Intel Arria 10 FPGAs for inferencing and what is the work flow behind it.

The remainder of this paper is organized as follows. Section 2 provides a survey of the recent and the state-of-the-art FPGA deep-learning acceleration tools that are available in research and commercially. In Sect. 3, the experimental setup is described, including the case-study models used for our study, and how they are pre-processed and trained in preparation for the Deployment and Inferencing stage. The three state-of-the-art DNN models used are HEP-CNN, CosmoGAN, and 3DGAN. HEP-CNN [19, 20] is a deep-learning model used by NERSC to identify new particles produced during collision events at particle accelerators such as the Large Hadron Collider (LHC). CosmoGAN [22], also under study by NERSC, is used to generate cosmology weak lensing convergence maps to study GAN model for science applications. The 3DGAN model [11] is a generative model under study by CERN openlab to replace the Monte Carlo method for particle collision simulations. Also in Sect. 3 is the description of the platform setup for FPGA-based inferencing. The hardware platform for the inference engine is the Intel Programmable Acceleration Card (PAC), equipped with an Arria 10 GX FPGA. The PAC card is installed in a Dell server equipped with an Intel gold-level Skylake CPU. Intel distribution of OpenVINO toolkit is used to optimize and deploy the trained models onto the FPGA.

In Sect. 4, we present and discuss the inference results in our study. First, the initial findings using the native DLA runtime are described. Next, we described how we used the Intel Deep Learning Accelerator (DLA) development suite to optimize existing FPGA primitives in OpenVINO to improve performance and develop new primitives to enable new capabilities for FPGA inferencing. For the scientific DNN models under study, we were able to demonstrate a speedup from 3x to 6x for a single Arria 10 FPGA against a single core (single thread) of a server-class Skylake CPU. The studies described in this section and a demonstration of the HGC workflow were submitted to and declared the winner of the first-ever Dell EMC AI Challenge in 2018 [1]. Finally Sect. 5 will provide the conclusions of the paper and a discussion of future work.

2 Related Works

Although CPUs and GPUs have been widely used for DNN inferencing, inference engines accelerated with FPGAs have recently emerged. Recent improvements in FPGA technologies greatly increased the performance for DNN applications, e.g., with a reported performance of 9.2 TFLOPS for Intel Stratix 10 FPGA [23]. Furthermore, FPGAs have other advantages important to many mission-critical applications such as low latency and energy efficiency. As a result, the amount of research and development on deploying and accelerating DNN models on FPGAs in recent years has grown, demonstrating great interest in both academia and industry. While some of the works focused on optimizing datapaths or computation algorithms for FPGA devices, many also involve developing tools for DNN model inferencing on FPGA platforms to provide a generalized framework for developers to build their customized applications.

One notable tool developed in the research community is PipeCNN [25], an OpenCL-based FPGA accelerator designed for large-scale convolutional neural networks (CNNs). The main goal of PipeCNN is to provide an FPGA accelerator architecture of deeply pipelined CNN kernels to achieve improved throughput in the inference stage. Unlike previous OpenCL design, memory bandwidth is minimized by pipelining CNN kernels. Efficiency is enhanced by using task-mapping techniques and data reuse. The PipeCNN architecture was verified by implementing two CNNs, AlexNet and VGG, on an Altera Stratix-V A7 FPGA, achieving a peak performance of 33.9 GOPS with a 34% resource reduction on DSP blocks.

Another notable FPGA-based inference tool is hls4ml from Fermilab [9], which is a deep neural network compiler based on HLS (High-level Synthesis language). The input to hls4ml is a fully connected neural network trained from conventional training frameworks such as Keras and PyTorch. The network is translated to Vivado HLS (from Xilinx) and then compiled for the target FPGA. For the first result in using this framework, the researchers focused on using FPGA for machine learning in an application of real-time event reconstruction and filtering in the Large Hadron Collider at CERN. The accessibility and ease of configurability in HLS allows for physicists to quickly develop and optimize machine learning algorithms targeting FPGA hardware.

The success of deploying and accelerating DNN models on FPGAs resulted in commercial offerings of these tools from both major FPGA vendors. OpenVINO, from Intel/Altera [15], is a comprehensive toolkit designed to support deep learning, computer vision, and hardware acceleration using heterogeneous (CPU, GPU, FPGA) platforms. The OpenVINO toolkit comprises of a Model Optimizer and an Inference Engine. The Model Optimizer takes, as input, a trained deep-learning model outputted from one of the supported frameworks (e.g., TensorFlow, Keras). It performs static model analysis and adjusts the deep learning model for optimal execution on end-point target devices, CPU, GPU, FPGA, or HETERO (CPU+GPU or CPU+FPGA). In this project, our focus is on the use of OpenVINO in the FPGA mode to accelerate the inferencing of state-of-the-art, scientific DNNs. OpenVINO and its components will be described in more details in Sects. 3 and 4.

With the recent acquisition of DeePhi, Xilinx provides the Deep Neural Network Development Kit (DNNDK)[8] to enable the acceleration of the deep learning algorithms in FPGAs and SoCs. At the heart of the DNNDK is the deep learning processor unit (DPU). The basic stages of deploying a deep learning application into a DPU are:
  1. 1.

    Compress the DNN model (using the Deep Compression Tool) to reduce the model size without loss of accuracy.

     
  2. 2.

    Compile the DNN model (using the Deep Neural Network Compiler) into DPU instruction code.

     
  3. 3.

    Create an application using DNNDK (C/C++) APIs.

     
  4. 4.

    Use the hybrid compiler to compile the hybrid DPU application.

     
  5. 5.

    Deploy and run the hybrid DPU executable on the target DPU platform.

     

The DNNDK deep learning SDK is designed as an integrated framework which aims to simplify and accelerate deep learning applications development and deployment for Xilinx DPU platforms.

3 Experimental Setup

As illustrated in Fig. 1, the heterogeneous computing workflow for DNN consists of three stages: (1) Data Analysis and Pre-processing, (2) Model Training, and (3) Deployment and Inferencing. In Sect. 3.1, we describe the three case-study models used for this project, and how they are pre-processed and trained in preparation for the Deployment and Inferencing stage. In Sect. 3.2, the platform setup for FPGA-based inferencing is described: hardware platform and the OpenVINO deployment tool. Inference results using OpenVINO are presented in Sect. 4.

3.1 Overview of Case Studies

HEP-CNN. HEP-CNN [19, 20] was developed as a proof-of-concept study for improved event selection at particle collider experiments. For example, at the Large Hadron Collider experiment (LHC) at CERN, protons are collided at almost the speed of light and disintegrated in the process, forming showers of particles which are detected by experiments such as ATLAS or CMS. These experiments generate large amounts of data in units of events, which correspond to a detector snapshot after a number of particle collisions. Most of the events can be explained by the well understood Standard Model of Particle Physics, also referred to as background. The challenge is to find and select events which potentially contain candidates for new physics. More specifically, HEP-CNN was designed to distinguish events containing r-parity violating supersymmetric particle signatures from background. It is comprised of 5 convolution and max-pooling layers with Leaky ReLU activations [12, 14]. The kernel and stride sizes are $$3\times 3$$ and $$1\times 1$$ respectively and it employs 128 filters per layer. The final set of layers consists of an average pooling across the dimensions output image followed by a fully connected layer with softmax activation which performs the binary classification. The training data was obtained by coupling the Pythia [24] event generator to the Delphes [7] fast detector simulator. The cylindrical data is represented as a 2D image of size $$224\times 224$$, where the two dimensions represent the binned azimuth angle and pseudorapidity [26] coordinates. The three input channels are given by the hadron and electromagnetic calorimeter energy deposits as well as the multiplicity of reconstructed tracks from the pixel detector. Trained using the ADAM optimizer [18], the model outperforms its benchmark, i.e. a hand crafted decision tree, by more than 2x in true positive rate at the same false negative rate.

Because of the lightweight and simplistic nature of the model as well as the importance of real-time event selection in particle detectors, we consider HEP-CNN a suitable prototype for inference performance exploration on embedded systems or deep learning accelerators.

CosmoGAN. Cosmological simulations of the $$\Lambda \mathrm {CDM}$$ model are traditionally very expensive: they consist of three dimensional n-body simulations followed by raytracing steps in order to obtain two dimensional weak gravitational lensing maps which are observed in large angle sky surveys. CosmoGAN [22] is a deep convolutional generative adversarial network (DC-GAN) which was designed to serve as a cheap emulator for these simulations. It is an unconstrained GAN which is able to reproduce these mass maps to very high statistical accuracy (cf. [22]) for a fixed set of cosmological parameters. The network input is a 64-dimensional vector of uncorrelated gaussian noise, followed by a fully connected layer to cross-correlate all inputs, followed by a series of four transpose convolutions, leading to a single $$256\times 256$$ output image. Each inner layer is batch-normalized [16] and uses Leaky ReLU activation, while the output layer uses a $$\tanh $$ activation. For more details on the network parameters cf. [22]. We decided to include this model into this paper because it is a scientific example of an important new class of generative deep neural network architectures. Another important aspect is that it does not require a data input pipeline, as the random numbers can be easily generated on the devices considered in this study. Therefore, it allows us to more precisely measure the compute and latency capabilities because the model is not limited by DRAM or PCIe bus bandwidth and latency.

3DGAN. 3DGAN represents the first application of three-dimensional convolutional Generative Adversarial Networks to the simulation of high granularity electromagnetic calorimeters. The aim of the study is to produce a network which can be passed as input a particle type, energy and trajectory, and which will produce an accurate simulation of the corresponding particle detector output. Our study is based on pseudo-data simulated with GEANT4 [4] in the proposed Linear Collider Detector (LCD) for the CLIC accelerator [21]. The LCD consists of a regular grid of 3D cells with cell sizes of 5.1 mm$$^3$$ and an inner calorimeter radius of 1.5 m. Individual electron, photon, charged pion, and neutral pion particles are shot into the calorimeter at various energies and at various angles to the calorimeter surface. For each event we take a $$25 \times 25 \times 25$$ cell slice of the electromagnetic calorimeter (ECAL) and store them as two 3D arrays containing information about the energy deposited in each cell. The 3DGAN generator and discriminator models consist of four 3D convolution layers. Leaky ReLU activation functions are used for the discriminator network layers. A batch normalization layer is added after all activations except the first layer. The output of the final convolution layer is flattened and connected to a sigmoid neuron corresponding to real/fake output of GAN as well as a linear unit for energy regression. The generator has a latent vector of size 128 and a similar architecture with leaky ReLU (ReLU for the last layer) activation functions. Batch normalization layers were added after the first and second layers. The GAN cost function was modified to include an auxiliary energy regression task as well as checks on total energy deposited in order to constrain the distribution of individual cell energies. The model is implemented using Keras and Tensorflow. The network is trained for 30 epochs using the RMSprop optimiser. Results show a remarkable agreement to standard Monte Carlo output (within a few percents) [11].

3.2 Platform Setup

As shown in Fig. 1, OpenVINO consists of two parts: Model Optimizer and Inference Engine. The OpenVINO software is built to emulate the Open Visual inference and neural network optimization. The OpenVINO toolkit extends the workload across Intel hardware and maximizes performance. The Model Optimizer is a cross-platform, command-line tool that facilitates the transition between the training and deployment environment on a target inference engine. The input to the Model Optimizer is a network model trained using one of the supported frameworks. It performs static model analysis and adjusts the input deep learning models for optimal execution on end point target devices, which can be a CPU, GPU, FPGA, or a combination (HETERO). The output of the Model Optimizer is an Intermediate Representation (IR) suitable as input to the selected target inference engine. In our study, our goal in the Deployment and Inferencing stage is to deploy the trained model on an FPGA to accelerate the classification process.

In addition to the trained model from the Model Optimizer, the other input to the OpenVINO Inference Engine is the data to be analyzed. The output is a probability-based classification. The Inference Engine is a C++ library with a set of C++ classes to infer data (images) to obtain a result. The C++ library provides an API to read the Intermediate Representation (IR), set the input and output formats, and execute the model on devices.

The hardware platform used in this study for the FPGA-accelerated inference engine is the Intel Programmable Acceleration Card (PAC). The PAC card contains an Arria 10 GX, a moderate-sized FPGA fabricated using 20 nm process technology. The PAC card is installed in a Dell server equipped with an Intel Gold 6130 Skylake CPU (14 nm process technology), running at a clock speed of 2.1 GHz. The Skylake is a dual-socket CPU, with 16 cores per socket, and 2 threads per core. Performance comparisons to be presented in Sect. 4 will be with a single Arria 10 FPGA versus different numbers of Skylake cores (threads).

4 Experimental Results

In this section, we present and discuss the inference results in our study. Section 4.1 discusses the initial findings using the native DLA runtime which was delivered with OpenVINO. In Sect. 4.2, we described how we used the DLA development suite (obtained from Intel via NDA) to optimize existing FPGA primitives in OpenVINO to improve performance and develop new ones to enable new capabilities for FPGA inferencing. The optimized results are presented in Sect. 4.3.

4.1 Native OpenVINO Results

Table 1 summarizes our initial inferencing performance results of two of the above scientific DNN models (HEP-CNN and CosmoGAN) using the OpenVINO toolkit with native Deep Learning Accelerator runtime.
Table 1.

Inferencing performance of HEP-CNN and CosmoGAN with native OpenVINO. (*HETERO: OpenVINO heterogeneous inferencing mode with FPGA + CPU)

DNN model

HETERO* throughput (images/s)

Speedup vs. CPU

1 core/1 thread

1 core/2 threads

32 cores/64 threads

HEP-CNN

66.3

2.52

1.32

0.25

CosmoGAN

4.7

0.21

0.11

0.03

Using the native DLA runtime, we cannot perform inferencing on either model completely on the FPGA. OpenVINO automatically use the HETERO (heterogeneous) mode with CPU as a fallback device on parts of the DNN which cannot be run on the FPGA. Still HEP-CNN achieved 2.52$$\times $$ speedup vesus the Skylake CPU (1 core/1 thread). Although having a regular AlexNet-like CNN topology, HEP-CNN could not be completely inferenced on the FPGA because of its unsupported (by OpenVINO) “average pooling” layer between the last convolutional and the fully-connected layer. Thus, during inferencing, OpenVINO automatically maps the average pooling layer onto the CPU and transfers outputs of the last convolutional layer to the main memory. It then transfers results back to the FPGA to complete its operation. This back-and-forth transfer between CPU and FPGA introduces a large overhead that negatively impacts the inferencing performance of the HEP-CNN model. An optimized result will be shown in Sect. 4.3.

The CosmoGAN model also cannot be completely inferenced on the FPGA due to the unsupported “deconvolutional” layers. As a result, the HETERO mode causes multiple data transferring between the FPGA and CPU (2N times), where N equals the number of deconvolutional layers in the model. This overhead is reflected in the extremely poor performance of CosmoGAN shown in Table 1.

In order to improve the performance, we optimized the inferencing of HEP-CNN and CosmoGAN by enabling the FPGA primitives (using the DLA developer suite - Sect. 4.2) for the “average pooling” layer and “deconvolution” layer, respectively. This optimization eliminates the back-and-forth, data-transfer overhead and greatly improve the inference performance. Design space exploration of the FPGA architecture was also performed to further improve the result (Sect. 4.3).

4.2 Deep Learning Accelerator Suite

In order to customize the FPGA architecture for our needs, we acquired the Intel Deep Learning Accelerator (DLA) developer suite, which is the underlying tool that enables inferencing of DNN models on FPGA devices with OpenVINO. DLA consists of a high-level API (DLIA plugin) that interacts with OpenVINO’s inference engine and an FPGA bitstream that creates the architecture shown in Fig. 2.
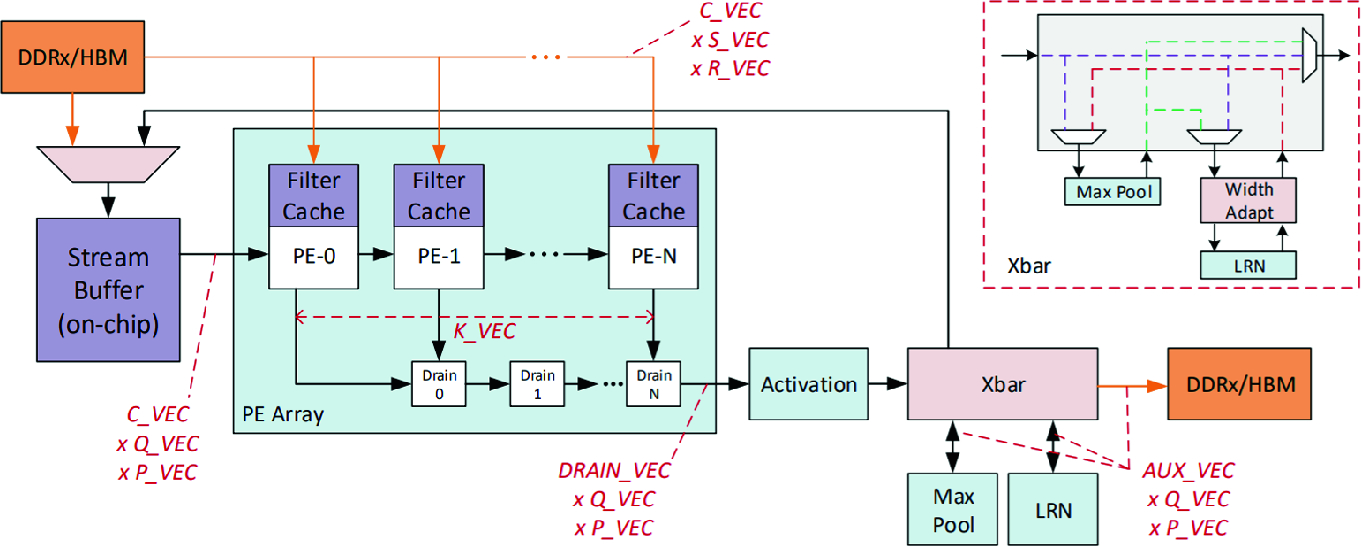
../images/491247_1_En_44_Chapter/491247_1_En_44_Fig2_HTML.png
Fig. 2.

DLA architecture [3]

The architecture contains a stream buffer, a PE (Processing Element) array, and various other modules that compute activation function, max-pooling, and normalization (LRN). The stream buffer takes advantage of the high bandwidth internal RAM of the FPGA, preparing the input data for the PE array. The PE array performs matrix multiplications and accumulations by utilizing DSP resource of the FPGA. DLA inferences a DNN model by first separating it into multiple sub-graphs, which typically consist of a convolutional layer, an activation layer, a max-pooling layer, and a normalization layer. The sub-graphs are then iteratively processed.

The DLA FPGA architecture (Fig. 2) can be customized for inferencing different DNN models. For example, DLA connects the max-pooling and the normalization modules to an “Xbar” module which can be configured to bypass or determine the execution order of pooling and normalization layers. It also allows the developer to create new primitives and connecting them to the “Xbar”. Moreover, the stream buffer size can be configured to reduce the number of memory requests to the main memory. The PE array can also be configured by changing “C_VEC” and “K_VEC” in Fig. 2. C_VEC defines the channel depth of the input data and convolution kernels streaming out from the stream buffer; while K_VEC defines the number of PEs in the PE array, which is also equivalent to the channel depth of the output data. Due to the resource constraint of the Arria 10 FPGA, DLA slices the input data along the channel dimension to complete the inferencing of a convolutional layer in multiple iterations. We will see in Sect. 4.3 how various configurations can affect performance.

4.3 Optimized Results

HEP-CNN. As mentioned in Sect. 4.1, the inference performance of HEP-CNN can be greatly improved by implementing the “average pooling” computation primitive on FPGA. By modifying DLA’s architecture configuration, we are able to enable the “average pooling” computation inside the “Pooling” module, as shown in Fig. 3.
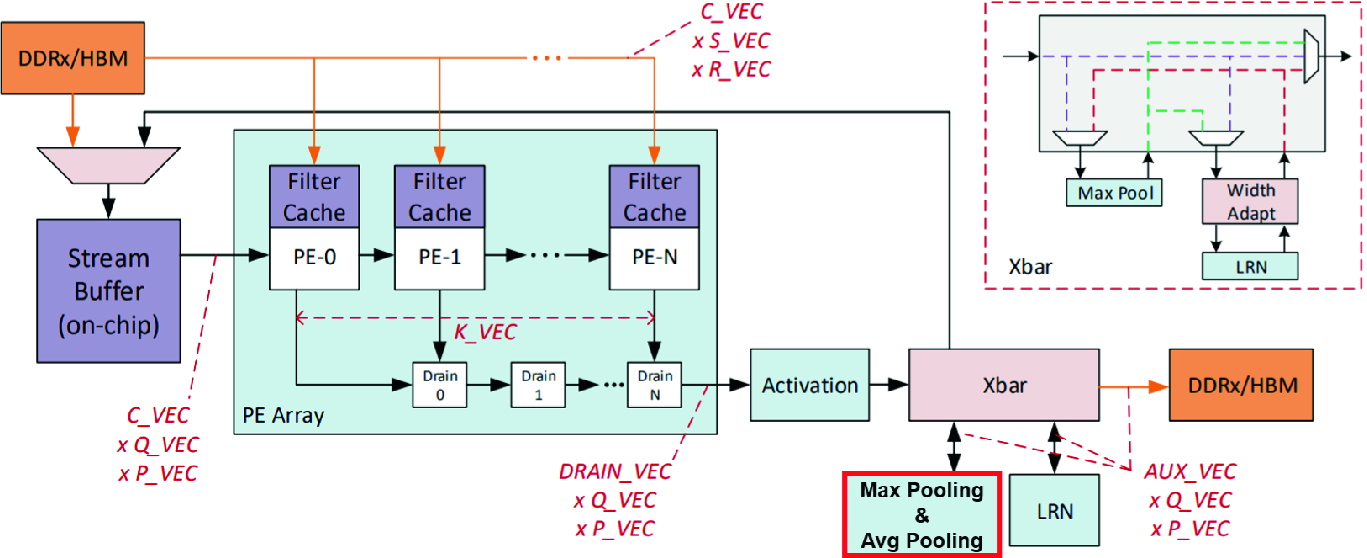
../images/491247_1_En_44_Chapter/491247_1_En_44_Fig3_HTML.png
Fig. 3.

Customized DLA architecture with average pooling enabled

The implementation of “average pooling” function eliminates the need of using OpenVINO’s HETERO mode and thus the overhead of data transfer between CPU and FPGA, improving the performance over that of the native architecture. We also performed design space exploration (size of the stream buffer, size (C_VEC) and number of PEs (K_VEC)) to further investigate the tradeoffs for HEP-CNN. Table 2 shows the comparison of the inferencing performance with different configurations for C_VEC and K_VEC. Also shown in Table 2 is the performance comparison for different configurations of the CPU:

  • 1 core, 1 thread: representing mission-critical applications with SWaP (space, weight, and power) constraints

  • 1 core, 2 threads (both threads in the core): represents applications in between

  • 32 cores, 64 threads: represents data-center applications

Table 2.

Comparison of inferencing performance of HEP-CNN with different configurations (batch size = 16)

PE array size (C_vec $$\times $$ K_vec)

FPGA throughput (images/s)

Speedup vs. CPU

1 core/1 thread

1 core/2 threads

32 cores/ 64 threads

8 $$\times $$ 48 (default)

138.4

5.26

2.76

0.55

8 $$\times $$ 64

164.9

6.27

3.3

0.66

16 $$\times $$ 64

148.2

5.63

2.96

0.59

Since all convolutional layers of HEP-CNN have an output channel depth of 128, as mentioned in Sect. 4.2, the default K_VEC value of 48 will cause DLA slicing the input data three times along the channel depth, resulting in $$ \displaystyle \frac{48\times 3-128}{48\times 3} = 11.1\% $$ wasting of computational resources. Thus, an optimal K_VEC should be one of the factors of 128 (e.g., 16, 32, or 64). It is also important to consider the balance of the resource consumption of the stream buffer and the PE array. Moreover, larger computing logic in the PE array could also results in a lower clock frequency in the FPGA as shown in Table 3.
Table 3.

Effect of PE array configuration on stream buffer size and clock frequency

PE array size (C_vec $$\times $$ K_vec)

Stream buffer depth

FPGA clock frequency

8 $$\times $$ 48 (default)

12768

252 MHz

8 $$\times $$ 64

11480

235 MHz

16 $$\times $$ 64

5040

190 MHz

CosmoGAN. For inferencing CosmoGAN on an FPGA, the deconvolutional layers need to be computed in the PE array. The term “deconvolutional” here does not refer to its mathematical definition, which defines the inverse of the convolutional operation. Instead, “deconvolution” often refers to the “transposed convolution” in deep learning literature and programming frameworks. Computation for DNN deconvolution is roughly equivalent to convolving an input signal with a transposed kernel [10]. Depending on its padding type and the number of strides, the input of a deconvolutional layer may also need to be zero padded and/or be dilated. Computing deconvolution for DNN by using convolution is illustrated in Fig. 4, which shows the deconvolution of a stride of 2 (Fig. 4(a)) is equivalent to the convolution of a stride of 1 with the transposed kernel and the dilated input.
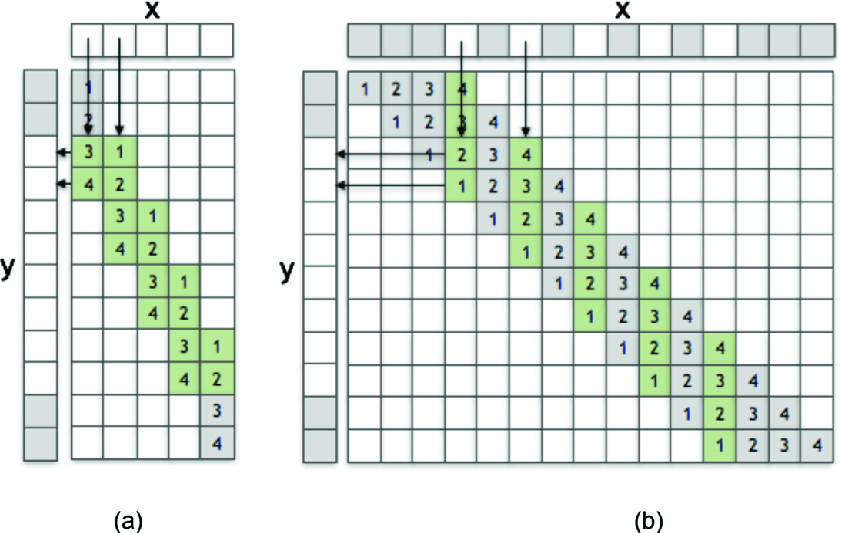
../images/491247_1_En_44_Chapter/491247_1_En_44_Fig4_HTML.png
Fig. 4.

(a) Deconvolution of stride 2 is equivalent to (b) Convolution of stride 1 with transposed kernel and dilated input

The DLA contains the primitive utilizing the PE array to compute deconvolution in the same way as computing regular convolution without changing its original logic and behavior. It also adds additional logic that transposes the weights matrix, and if needed, adds zero padding and dilates the input before streaming them into the PE array. Table 4 shows the inferencing performance of CosmoGAN model after we have made the enhancements to enable the deconvolution primitives in the DLA architecture configuration.
Table 4.

Comparison of inference performance of CosmoGAN.

PE array size (C_vec $$\times $$ K_vec)

FPGA throughput (images/s)

Speedup vs. CPU

1 core/1 thread

1 core/2 threads

32 cores/64 threads

8 $$\times $$ 48 (default)

22.2

0.98

0.52

0.14

8 $$\times $$ 64

24.2

1.07

0.57

0.16

16 $$\times $$ 64

19.9

0.88

0.47

0.13

Table 5.

Comparison of inferencing performance of CosmoGAN after switching the execution order of activation layer and normalization layer

PE array size (C_vec $$\times $$ K_vec)

FPGA throughput (images/s)

Speedup vs. CPU

1 core/1 thread

1 core/2 threads

32 cores/64 threads

8 $$\times $$ 48 (default)

39.4

1.74

0.92

0.25

8 $$\times $$64

67.5

2.97

1.58

0.43

16 $$\times $$ 64

39.9

1.76

0.93

0.26

As you can see, the performance on FPGA for CosmoGAN is very poor. Upon further investigation, we determined the DLA architecture has a limitation that the “activation” layer is hardwired to the PE array so it has to be executed before the “pooling” or “normalization” layer within one sub-graph (see Fig. 2). This architecture makes sense for many mainstream CNN model, but not for models such as CosmoGAN which implements the normalization layer before ReLU activation. As a result, using the current DLA architecture, the CosmoGAN DNN has to be inferenced in two separated iterations. We hypothesize that this limitation caused the FPGA performance to be reduced by half. To confirm this hypothesis, we manually switched the execution order of normalization and activation layers in the CosmoGAN model, simply for the purpose of exploring the theoretically best inferencing performance of CosmoGAN on the FPGA. Of course, the actual classification will not be correct, but the inferencing process should require the same amount of computation. The corresponding performance results are shown in Table 5, which are consistent with our expectation. The new speedup against 1 Skylake CPU core (1 thread) is approximately 3$$\times $$. Note the speedup against the HETERO mode (FPGA + CPU in Table 1) is 14$$\times $$.

5 Conclusions and Future Directions

Heterogeneous computing (HGC), using CPUs integrated with accelerators such as GPUs and FPGAs, offers unique capabilities to accelerate DNNs. In this paper, we presented an HGC workflow in performing deep learning studies on scientific DNN models. In particular, we focused on the use of Intel’s OpenVINO to facilitate the use of FPGA-accelerated inferencing on the HEP-CNN and CosmoGAN models from NERSC (Lawrence Berkeley Lab) and the 3DGAN model from CERN openlab.

From the results presented in Sect. 4, we demonstrated that, for scientifically relevant DNN models such as HEP-CNN and CosmoGAN, a single Arria 10 FPGA (20 nm technology) can produce speedups of 6$$\times $$ and 3$$\times $$, respectively, against a single core (single thread) of a server-class CPU (Skylake CPU, 14 nm technology). Going forward, from a FPGA device point of view, we are looking forward to working with the PAC card equipped with an Intel Stratix 10 (14 nm technology).

From a framework and tools point of view, the lessons learned thus far in using OpenVINO and the DLA development suite will be invaluable in our effort to enhance the DLA primitives and architecture to support existing and emerging scientific DNN models and applications. In particular, we have been developing the necessary primitives to support the 3DGAN model from CERN openlab.

Finally, the results from this study, as exemplified by the results presented in Sect. 4, provide an excellent foundation for more extensive data space exploration going forward to investigate various architectural, model, and tool tradeoffs on performance and other important metrics such as power and cost.

Acknowledgement

This research is funded in part by the NSF SHREC Center and the National Science Foundation (NSF) through its IUCRC Program under Grant No. CNS-1738420; and by NSF CISE Research Infrastructure (CRI) Program Grant No. 1405790.