14
Grammar and Grammatical Statements

SEVERIN SCHROEDER

1 Grammar: The Rules of Language

“Grammar” is Wittgenstein’s preferred term for the workings of a language: the system of rules that determine linguistic meaning. A philosophical study of language is a study of “grammar,” in this sense, and insofar as any philosophical investigation is concerned with conceptual details, which manifest themselves in language, it is a grammatical investigation.

In the Tractatus Logico‐Philosophicus Wittgenstein offered a mathematical picture of language: presenting language as a calculus. The essence of language, the general form of the proposition was given by a simple formula (TLP 6). Like a calculus, language was claimed to be governed by syntactic rules: (i) formation rules about the licit combination of names to form elementary propositions; (ii) formation rules about the licit combination of elementary propositions to make complex propositions; and finally (iii), truth‐table rules, which enable us to identify logical truths and entailments. Notoriously, the existence of the first type of rule remained a postulate. As no examples of actual names were given, the rules governing their use could of course not be presented either. Moreover, Wittgenstein insisted rather perversely that no syntactic rule could be meaningfully stated.

When Wittgenstein grew dissatisfied with this view of language, it was not the idea that language was essentially rule‐governed that he found fault with. On the contrary, that idea he held on to emphatically at least until about 1936, only correcting his account of what those rules were and how they functioned. In fact, it would not be much of an exaggeration to say that Wittgenstein’s break with his early philosophy was largely due to a careful reconsideration of the role of rules in language. Roughly speaking, while the author of the Tractatus thought that rules could work in secret and that their workings had to be discovered and analyzed (just as one has to discover and analyze invisible chemical processes), the Wittgenstein of the 1930s realized that language is an artifact and to the extent to which it is governed by rules, those rules must be made and applied by us (BB 27 f.; BT 268). Hence the idea that those rules could to a large extent be unknown to competent speakers and awaiting to be unearthed by future logicians (cf. TLP 4.002) must be absurd — “a hellish idea,” as Wittgenstein now called it in conversation with Friedrich Waismann (WVC 129 f.) – just as absurd as the idea that nobody yet knows exactly what the rules of football are. Indeed, the comparison between language and a game becomes one of the leitmotivs of Wittgenstein’s later philosophy, as suggested by his concept of a language‐game. The title of Chapter 45 of the so‐called Big Typescript makes his new view explicit:

Language functions as language only by virtue of the rules we follow in using it, just as a game is a game only by virtue of its rules. (BT 196)

Rejecting the idea of postulated “subterranean” rules, not known to those who follow them, and focusing instead on rules that are actually manifest in our ordinary language use Wittgenstein became aware of the contingency of some of those rules: the fact that different languages with significantly different rules are at least conceivable. By contrast, in the Tractatus Wittgenstein had presented logical syntax as the essence of any possible language (see Hacker, 1972/86, p.181).

Moreover, attention to actual linguistic detail made Wittgenstein realize that ordinary language is a good deal less tidy, less precisely regulated than a calculus. While the author of the Tractatus had insisted on the determinacy of sense and on perfect linguistic precision, appearances to the contrary notwithstanding, the later Wittgenstein rejected this ideal as a prejudice and declared that our grammatical rules are often vague. He now states explicitly that there is no logical calculus underpinning our language, although we may conveniently use such a calculus as an object of comparison:

remember that in general we don’t use language according to strict rules – it hasn’t been taught us by means of strict rules, either. We, in our discussions on the other hand, constantly compare language with a calculus proceeding according to exact rules. (BB 25; cf. PI §81)

Indeed, the rules that could be written out to reflect the meanings of our words are not only vague, our lists of such rules would also remain incomplete: the game which we play with words “is not everywhere circumscribed by rules” (PI §68). For example, we have no rules by which to decide how the word “chair” is to be applied to chair‐like objects that keep disappearing like hallucinations (PI §80).

Finally, it is noteworthy that in the Tractatus account there is no mention of semantic rules. Logical grammar, for the young Wittgenstein, is only logical syntax (TLP 3.325); and logical syntax can be determined without paying any attention to the meaning of the signs (TLP 3.33). The connection between a name and its meaning, that is, the object named, is not fixed by a rule, but by a mental act of meaning (NB 104, 130; cf. PG 97). (Hence, Wittgenstein will spend a lot of time in his later philosophy exorcising this idea that linguistic meaning depends on mental processes of meaning something.) In the 1930s, by contrast, Wittgenstein’s concern with linguistic rules is mainly focused on semantic rules, explanations of the meanings of words, which are now emphatically included in grammar:

There is not grammar and an interpretation of signs. Rather, in so far as one can talk about an interpretation, i.e. an explication of signs, it is grammar itself that has to take care of that. (BT 58)

Even ostensive explanations, such as “This colour → 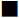images is called ‘black,’” are now regarded as rules of grammar (BT 199, 234; PG 88), which is not an entirely felicitous use of the term. An ostensive explanation can perhaps be called a “rule” if it involves a canonical sample (such as the standard meter in Paris). Ordinary ostensive explanations, however, that explain a word by pointing to whatever suitable instance of the concept is at hand, are more plausibly regarded as explanations by example than as rules. The difference between these two types of explanation is that statements of rules, unlike instantiations, are not themselves “moves in the game.” Thus, to explain the waltz by giving a list or diagram of the correct steps can be called: giving a rule. The explanation is not itself a performance of the dance. But one can also teach the waltz by giving the learner a demonstration of it. This would not be a rule, but an explanation by example. For the instructor’s teaching is itself an instance of dancing the waltz, a “move in the game.” Similarly, a casual ostensive explanation of the word “purple” by pointing at and naming the color of a violet is simply an instance of a correct application of the word (“This flower is purple”); and as such it is already a move in the language‐game (teaching by doing) (cf. Schroeder, 2001).

Wittgenstein admits that the way he uses the term “grammar” differs from common usage (MS 110, 195; AWL 31). Explanations of word meaning, as given in dictionaries, are not normally subsumed under grammar. On the other hand, the usual morphological concerns of grammarians – declination, conjugation of irregular verbs, tense, gender, and word order – the stock in trade of school grammar, is quite irrelevant to philosophical investigations of language. The key difference lies in the aims for which the study of language is pursued by the linguist and the philosopher. The philosopher does (or should) not attempt to give a comprehensive and detailed picture of language for its own sake. Rather, philosophical attention to language is just a means to resolving philosophical problems. Hence philosophical accounts of grammar can ignore most areas of school grammar, but have to focus on the relations between some interesting concepts and their criteria of application. Thus a philosopher’s grammatical investigation bears more resemblance with the work of a lexicographer than a grammarian, yet it is extremely selective and often pays attention to aspects of a word’s meaning that are not spelled out in a dictionary.

2 The Autonomy of Grammar

“Grammar,” writes Wittgenstein in an important passage in the Big Typescript, “is not accountable to any reality. The rules of grammar determine meaning (constitute it), and therefore they are not answerable to any meaning and in this respect arbitrary” (BT 233). In the early days of developing his conception of grammar (1929–1933), Wittgenstein suggested the following argument for the arbitrariness, or autonomy of grammar:

The conventions of grammar can’t be justified by a description of what is represented. Any description of that kind already presupposes the rules of grammar. (BT 238)

This is a rather odd way of putting it: if something is a convention then of course it can’t be justified as being true to the facts. The idea seems to be that one may mistakenly think that it is not a convention, but a metaphysical truth. Wittgenstein gives the example “There are only four primary colours” (BT 236; Z §331), which however is difficult to assess as there are different concepts of a primary color. But in the same passage he considers the idea that colors must be classified together, because they are similar, “as opposed to, say, shapes or tones”; and he suggests the response that this similarity is only the result of our classification and so cannot be invoked to justify it (BT 237). But that is hardly convincing. The obvious difference between red and green, on the one hand, and C and D, on the other, is that the former can only be seen and the latter can only be heard. Stating it does not presuppose the concept of a color. Of course it would be possible, as Wittgenstein suggests in the following sentence, to have a concept of something being red, green, or circular. But even familiarity with such a classification, instead of that of a color, would not change the fact that there is a difference between red and green, on the one hand, and circular, on the other: if a surface is entirely red (or green), every visible part of it is red (or green); yet if a surface is circular it doesn’t follow that a part of it must be circular too. Moreover, red and green are mutually exclusive, while they are both combinable with circularity.

In a related passage it is claimed that:

If I could describe the purpose of grammatical conventions by saying that I had to create them because, for instance, colours have certain properties, that would make these conventions unnecessary. (PR 53; BT 238)

Here one could object that if a convention was prompted by certain similarities it would not for that matter be superfluous. That colors have something in common that justifies grouping them together doesn’t mean that conventionally doing so (classifying them under one label) isn’t a useful convention. After all, there are plenty of cases of things having features in common that we do not bother to pick out by a single word (e.g., trees and bushes with serrated leaves).

However, the continuation of the passage quoted suggests that Wittgenstein had a different kind of case in mind, namely that of a convention laying down, or implying, what combinations of words do and don’t make sense:

That would make these conventions unnecessary, because then I could say precisely what it was the conventions were excluding. Conversely, if the conventions were necessary, i.e. if certain combinations of words had to be excluded as being nonsensical, then for that very reason I couldn’t name a single feature of the colours that would make the conventions necessary, for then it would be conceivable that the colours might not have that feature, and that could only be expressed by contravening the conventions. (PR 53; BT 238)

To begin with a different example, it is surely correct that one cannot justify the semantic convention that the word “bachelor” applies to unmarried men by insisting that bachelors really are unmarried men. That all bachelors are unmarried men by definition can obviously not explain why we chose that definition of the word. However, Wittgenstein’s example of the concept of a color is less straightforward, since it is not defined in terms of certain features, but by a list of instances: red, green, blue, yellow, etc., are colors. Now the question may arise as to why, for example, heavy or circular are not classified as “colors” as well; and one may suggest the answer that colors are perceptible by sight only, which rules out weight or shapes. Arguably, this feature of being perceptible by sight only is not a defining feature of color: we do not present it as a criterion when teaching the word. Rather, it is something we realize afterwards when considering the familiar instances of particular colors. Hence it can appropriately be cited to justify the list of particular colors that serves us as a definition. That list is indeed more natural and practical than an alternative list of classification subsuming: red, green, blue, heavy – for these do not all share the feature of being perceptible by sight only.

But to this Wittgenstein might object as follows: we cannot say that colors have the feature of being perceptible only by sight, which makes our classification sensible, “for then it would be conceivable that the colors might not have that feature, and that could only be expressed by contravening the conventions.” — However, this objection appears to be based on the Tractatus dogma that for a statement to be meaningful its negation must be meaningful too, and that therefore you cannot really express any necessary truths. But that is a dogma we should not accept. Of course you can meaningfully say, for example, that colors are visible. That the negation of such a claim is nonsense doesn’t make it unsayable, it only shows it to be a characterization of the concept of a color, rather than an empirical claim. Admittedly, such a characterization of a concept must be a consequence of the way that concept has been defined or fixed; but since it need not be explicit in the concept’s definition or explanation, it may well be licit to invoke it in order to justify the concept.

Even if Wittgenstein’s argument for the autonomy of grammar fails to convince, there are three other considerations that strongly support the view that grammar is not determined by reality and cannot be faulted by it, even though it may be possible to justify some concepts as more natural and more useful than others (see also Chapter 15, THE AUTONOMY OF GRAMMAR). (That, contrary to some of his earlier remarks, experience can in a certain way be said to justify our grammar is shown by Wittgenstein’s account of arithmetical equations as grammatical rules (see section 6 below). If the objects we count were so unstable or evanescent that after adding 7 of them to 5 others we did not regularly count 12 in all, the equation “7 + 5 = 12” would be useless as a grammatical norm (RFM 52). Hence, the empirical fact that such counts do almost always yield the result that the corresponding equation makes us expect provides some justification for holding on to the grammar of our arithmetic.)

First, “the rules of grammar determine meaning (constitute it), and therefore they are not answerable to any meaning” (BT 233). Of course, if the meaning of a word is its conventional use in the language (PI §43; cf. Schroeder, 2006, ch.4.4), then a rule suggested to capture that use can be found correct or inaccurate. But taking “the rules of grammar” to be the norms that inform our use, there is no meaning independent of them (BB 28). In particular, where on different occasions or in different contexts a word is used according to different rules, it makes no sense to suggest that some are and some are not in agreement with the word’s true meaning. Thus, the meaning of the word “not” does not compel us to take double negation as affirmation; we could also take it as emphatic negation. Each option gives the word “not” a slightly different meaning (BT 234).

Secondly, there is no extralinguistic purpose determining the correct rules of language. One can of course say that language is a means of communication. A system of vocal sounds to be produced according to certain rules, but unsuitable for any communicative purpose, we would probably not call a language (it might be a kind of phonic game). But then, not every use of language is an act of communication (soliloquies are the most obvious counterexample), and communicative success is not by any means the only thing that matters to us about language (various aesthetic considerations are taken very seriously too). Hence suitability for communication may be a minimal requirement for any kind of language, but the concept of communication is immensely wide and compatible with an endless range of different grammatical rules and conceptual schemes. It would certainly not allow us to determine any specific set of concepts as the correct ones.

At one point Wittgenstein contrasted grammatical rules with the rules of cooking, suggesting that “‘cookery’ is defined by its end, whereas ‘speaking’ is not”:

You cook badly if you are guided in your cooking by rules other than the right ones; but if you follow other rules than those of chess you are playing another game; and if you follow grammatical rules other than such‐and‐such ones, that does not mean you say something wrong, no, you are speaking of something else. (BT 237; Z §320)

But the contrast is not as neat as this passage suggests. Which are the “right” rules of cooking? There is an endless variety of culinary procedures. Of course where the result of applying a rule is something absolutely unfit for human consumption, we wouldn’t call it a rule of cookery. But then, similarly, a rule for producing certain vocal utterances would not count as a grammatical rule if those utterances were just meaningless sounds. In fact, the relation between rules of cookery and nutrition is fairly similar to that between rules of grammar and communication. In both cases, the former are restricted, but not determined by the latter. (The rules of chess are of course not to be compared to the rules of cooking, but, say, to the rules of cooking a Mushroom Stroganoff according to a particular recipe, for instance, Jamie Oliver’s Wild Mushroom and Venison Stroganoff for Two Lucky People (2008) – and again, the analogy holds: if you don’t follow the recipe, you don’t necessarily cook badly, you’re just preparing a different dish.)

Thirdly, contrary to a widespread philosophical view, our concepts are not determined by the essences of things. This ought to be self‐evident, simply a consequence of the trivial fact that language is man‐made and conventional (BB 27 f.). We are obviously free to decide that all objects of a certain description are to be called by a label of our invention. Thus I could stipulate that whatever is either red, green, or circular is to be called “gog” (cf. BT 237). As a stipulation this may be criticized as impractical or useless, but not as false (BT 236). Unlike propositions or declarative sentences, concepts are not truth‐apt. However, the widespread idea of a natural kind concept is an attempt to deny this. To describe a concept as of a natural kind is to make the implicit claim that its classification is scientifically correct. So‐called scientific realists believe that on the micro‐level (of DNA or atomic structure) nature herself determines how things are to be correctly classified. But that is naive, for apart from the fact that it is still our decision to take anything on the micro‐level into account (and for many purposes we don’t), down there we are just as much overwhelmed with data and still have to decide which ones (which of an animal’s 30 000 genes, for example) are to be relevant to classification. There is no getting away from the fact that words and their meanings are our artifacts and we have to take responsibility for them.

3 From Rules to Norms

It has already been mentioned above that in his later discussions Wittgenstein no longer believes that language is, like a calculus, a complete system of exact rules. Indeed, he becomes increasingly critical of the idea that language is, like a game, strictly speaking rule‐governed, entering some further important reservations:

Linguistic rules are not normally part of the game (“an instrument of the game itself” (PI §54; cf. §82)) in the way they are in some of Wittgenstein’s simplified language‐games. He imagines, for example, that someone is given a table correlating letters and movements and then a sequence of letters as an order to move in a certain way (EPB 139). To carry out the order one consults the table, that is, the rule. By contrast, if someone directs me in English (“Right. Straight on to the traffic lights, then second left.”) I do not consult a rule to derive my movements from his words.
We have not been taught our mother tongue by rules (cf. PI §54). And this is an important point for Wittgenstein, for he identifies as a typical philosophers’ mistake an inclination to describe our learning of language in a way that already presupposes linguistic competence, like the learning of a foreign language (PI §32). Therefore he emphasizes that at the basic stages language teaching cannot be explaining, let alone giving rules, but must be training or drill (“Abrichtung”) (PI §6; cf. MS 179, 7v: “To follow a rule presupposes a language.” [“Einer Regel folgen setzt eine Sprache voraus.”]). And even at later stages, language is for the most part learnt by picking up a sufficient number of examples of correct usage, rather than by rules or explicit explanations. “One learns the game by watching how others play” (PI §54).
Hence linguistic rules for natural languages are not necessary for the actual use of a language; they are only summarizing descriptions of that use (PI §54). As such they can still be called “rules of grammar,” but then the latter word is taken in a different sense: referring not to the actual workings of language, but to a systematic account of those workings. “Grammar,” Wittgenstein remarks, using the word in this derivative sense, “is a description of language ex post” (“Die Grammatik ist eine nachträgliche Beschreibung der Sprache.”: MS 110, 110). It is of course true that linguists’ systematic descriptions of a language, in dictionaries and grammar books, will subsequently have a normative and stabilizing impact on certain aspects (usually fairly subtle aspects) of the use of language by educated speakers; but this is a feature of a highly advanced and sophisticated literary culture. It is clearly not essential to the phenomenon of language and, from a historical point of view, would not have been relevant for most speakers of most languages for most of the time.
Taking the points made so far into consideration, Wittgenstein withdraws his earlier claim that “language functions as language only by virtue of the rules we follow in using it, just as a game is a game only by virtue of its rules” (BT 196). In a handwritten note he comments:
That is not correct, in so far as no rules have to have been laid down for language; no more than for a game. But one can look at language (and a game) from the standpoint of a process that uses rules. (BT 196)
The rules of a language, he now suggests, are a useful fiction, like that of a social contract:
“Contrat social” – here too no actual contract was ever concluded; but the situation is more or less similar, analogous, to the one we’d be in if … And there’s much to be gained in viewing it in terms of such a contract. (BT 196v)
It is, after all, a fact that language involves normativity. We do not only use certain expressions, we regard them as correct, and we criticize and reject others, which we regard as incorrect. This important feature of language is rightly emphasized by comparing language to a rule‐governed game, even if the comparison does not give an accurate picture of the way linguistic normativity is conveyed and implemented.
Wittgenstein’s reservations go further still. Acknowledging that linguistic rules need not actually be consulted, but may be nothing but summary descriptions of people’s use of words, he writes (in 1933–1934):
But what if observation does not enable us clearly to see any rule, and the question [put to a speaker as to what rule he follows] brings none to light? – For he did indeed give me an explanation when I asked him what he understood by ‘N’, but he was prepared to withdraw and alter it. – So how am I to determine the rule according to which he is playing? He does not know it himself. Or, more accurately: What meaning is the expression ‘the rule by which he proceeds’ supposed to have left to it here? (PI §82; cf. BB 25)

Wittgenstein seems to envisage two reasons why in many cases no rule can be given. One is illustrated in the following section by an analogy with games:

Doesn’t the analogy between language and games throw light here? We can easily imagine people amusing themselves in a field by playing with a ball so as to start various existing games, but playing many without finishing them and in between throwing the ball aimlessly into the air, chasing one another with the ball and bombarding one another for a joke and so on. […]

And is there not also the case where we play and – make up the rules as we go along? And there is even one where we alter them – as we go along. (PI §83)

The idea seems to be that a variety of different language‐games can be played with the same words and that (unlike the builders of §2 of the Investigations who always use the same words in the same way) we tend frequently to move between them, mix them up, and introduce new variations (cf. BB 28: “there are words […] which […] are used in a thousand different ways which gradually merge into one another”). Picking out one of those uses, we might well be able to produce something like a rule, but then it will not be applicable to what we do with the same expression in another context. So we’d have to “withdraw and alter” our explanation; and will do so again when considering yet other uses. Our grip on linguistic normativity is essentially piecemeal, and the explanations that we can give manifesting our linguistic competence are always just provisional, read off from some language‐game which could easily on another occasion shade into, or be developed into, a slightly different one.

The most telling expression of Wittgenstein’s claim that linguistic normativity is often piecemeal is of course his introduction of the idea of a family‐resemblance concept. He suggests that when we try to formulate a comprehensive rule, that is, a definition, for the use of the word “game,” we draw a blank (PI §66). Here, as in many other cases, what is subsumed under a given concept cannot be derived from a general rule, for it has not been decided once and for all, but case by case, according to the way the concept was first introduced with only some applications in mind, and then applied or not applied to new kinds of cases, as people saw fit. Thus, for example, tennis is called a game, whereas judo is not, although they are both competitive rule‐governed sports.

Taking stock of Wittgenstein’s qualifications of the idea of language as rule‐governed, we should, however, be careful not to throw the baby out with the bath water. The essential normativity of grammar is never called into question. It is certainly true that our use of language manifests linguistic norms. Often, though not always, they can be given in the form of rules: general statements summarizing how an expression is to be used (e.g., definitions). But such rules are, for the most part, only ex‐post abstractions from actual usage (unlike the rules for a calculus, laid down beforehand). In order to acknowledge all the qualifications and reservations Wittgenstein had about speaking of rules of language, while holding on to his crucial insight into the normativity of language, it may be better to speak of the norms of language, with the proviso that norms can be piecemeal and implicit in a practice, and need not be laid down as general verbal expressions, i.e., as rules.

4 Rules of Grammar and the Discussion of Rule‐Following

One may well wonder why, if by the mid‐1930s Wittgenstein had so many reservations about regarding language as rule‐governed, he should have spent so much time in Philosophical Investigations discussing what it is to follow a rule.

Trying to answer this question, we should first of all note an important point about Wittgenstein’s use of the word “rule” in the Investigations, which is clarified by a passage in “The Brown Book.” There he distinguishes between two kinds of (what he calls) rules, namely: semantic rules and instruction rules (BB 96, 98; cf. EPB 140, 143). A semantic rule gives the meanings of signs, e.g., in the form of a table:

move to the right
move to the left
move forward
move backward.

Using those signs to give somebody an order (e.g.: “c a d a”) would rely on the previously given rule, but it would not itself be a rule. However, where such an order is meant to be followed again and again, say, in drawing a continuing ornamental pattern, Wittgenstein is happy to call it a “rule,” too. It is what may be called an instruction rule:

In this case I think we should say that “cada” is the rule for drawing the design. Roughly speaking, it characterizes what we call a rule to be applied repeatedly, in an indefinite number of instances. (BB 96)

This, I think, helps us to understand what is going on in the rule‐following discussions in the Investigations. What I presented above were Wittgenstein’s misgivings about the idea of semantic rules, but what occupies him in the Investigations under the title “following a rule” is something different: it is not semantic rules, but instruction rules, that is: orders to continue doing something in a regular manner, e.g., writing down series of numbers. (Note how often he uses the word “order” together with or instead of the word “rule”, e.g.: PI §§186–9, 206, 212; cf. MS 165, 40; 84.)

Why then should Wittgenstein be interested in such orders? — Because his main concern in those parts of the book is the concept of understanding. And orders and their execution provide the most straightforward and most perspicuous example of semantic understanding (cf. MS 165, p.30). If you make a statement, giving me a piece of information, my understanding may or may not show in my behavior. Telling me that it is snowing may make me go out or not, depending, amongst many other things, on whether I like to be out in the snow or not. In that way, most linguistic understanding has no direct behavioral manifestation. Orders given to somebody assumed to be willing to comply are rather different. Understanding or misunderstanding show immediately in what is done. At this point language comes into direct contact with action. Hence Wittgenstein’s preference for language‐games of ordering, such as buying apples (PI §1) or directing an assistant to pass building material (PI §2).

Moreover, Wittgenstein had a particular interest in an understanding that goes beyond a particular occasion, such as the understanding of a system (PI §143). For one thing, because such an understanding of complex, possibly even infinite contents seems particularly puzzling, especially as it can happen in a flash. We are inclined to think of understanding as having mental representations; yet how can a highly complex system be represented instantaneously in one’s minds? (see Schroeder, 2006, pp.181–97). — For another thing, linguistic understanding is obviously systematic. We do not just understand single utterances (tokens); we understand types of words and expressions, such that we know how to apply them or how to respond to them again and again, on an endless number of occasions.

So, there is no tension between Wittgenstein’s reservations about the importance of semantic rules and his intensive discussion of following rules; because the well‐known examples of rule‐following in the Investigations (continuing arithmetical series) are not concerned with semantic rules. They are just cases of carrying out orders with an endless applicability. As such they are just variations of the builders language‐game: “Write down the series of even numbers!” is like “Keep bringing me slabs!” (Cf. RFM 341c–f, where “How can I follow a rule?” and “How do I know what to do in response to the order ‘slab!’?” are treated as on a par.)

The deviant pupil of §185 could just as well have been presented as a deviant builder’s assistant who when given the order “slab” for the fifth time brings a block, etc. — So it’s not that all linguistic understanding is a form of rule‐following; rather: following rules of instruction is just one simple type of linguistic understanding, one language‐game.

There is, however, more to be said about the relation between Wittgenstein’s misgivings about semantic rules and his discussion of rule‐following. As I said, his concern with understanding how to continue an arithmetical series is that, in this case, one’s understanding must cover an infinity of instances. How is that possible? How can an infinity be grasped in an instant? The most natural answer is that such understanding can only be achieved by means of a general rule or formula, which although easily grasped in a moment can determine an infinity of instances.

So, what those discussions in the Investigations are meant to investigate is the possibility of an endlessly applicable understanding. That is the explanandum, the common phenomenon that needs to be clarified. Rules or formulas are only considered as an explanans, as a suggested solution – which is shown not to work: our understanding cannot be based on rules. No rule can guarantee understanding: we still have to know how to apply it in any given case. Thus the puzzle about the infinity of instances resurfaces as a puzzle about the infinity of applications of a rule. Of course it is possible to learn how to apply a rule to indefinitely many cases. But ultimately, our mastery of rules has to be grounded in an ability to continue in what we regard as a regular manner that is not guided by any rule, but can only be taught by examples (MS 136, p.124a; Z §§300–1; see Schroeder, 2006, pp.181–97).

Hence, although Wittgenstein was certainly no skeptic about the possibility of following a rule, it can be said that his reservations about the importance of linguistic rules dovetail neatly with his discussions of continuing an arithmetical series. While earlier he argued that rules are not necessary for understanding general notions (cf. Z §295), now he shows that rules are not sufficient for such understanding either. Even if there are linguistic rules, ultimately they cannot be the foundation of linguistic normativity. What is held up both as an alternative to and as a basis for rules is the kind of know‐how that is acquired through examples and training.

5 Grammatical Statements and Analytic Truths

Wittgenstein speaks not only of “grammatical rules,” but also of “grammatical statements” (or propositions) (grammatische Sätze). The difference between the two concepts is one of perspective: linguistic meaning can be explained by grammatical rules (or, to take Wittgenstein’s own qualifications into account, by expressions of grammatical norms). For example, the meaning of the word “bachelor” can be explained by the grammatical rule:

(1) A bachelor is an unmarried man.

However, when this sentence is not used to teach or to explain, but considered as a statement, Wittgenstein calls it a grammatical statement. After all, we regard it as true that a bachelor is an unmarried man, which makes it more natural to speak of a statement (or proposition) than a rule. It is a statement, but not an empirical statement, not a “statement of fact” (AWL 18); it is “a statement which no experience will refute” (AWL 16). The nonempirical nature of such a statement can be brought out by a modal verb: “if someone’s a bachelor, he must be an unmarried man.” And yet we ought not to yield to the philosophical temptation of regarding such a nonempirical statement as metaphysical, as a statement of a super‐fact, as it were (cf. BB 54 f.). Rather, its necessity is that of a norm of expression (AWL 16).

My hackneyed example (1) is a grammatical statement, yet it can also be regarded as a grammatical rule, even in the light of Wittgenstein’s reservations about that concept. It provides a general, but handy description of the use of the word “bachelor,” suitable for linguistic instruction. However, many of the grammatical statements Wittgenstein has occasion to consider in the course of his philosophical investigations one would not normally call rules of language, e.g.:

(2) Behind the utterance of a sensation there is nothing [no object]. (MS 124, p.6)

(3) Of course I know what I wish. (BB 30)

(4) My reason for saying that I see is not the observation of my behaviour. (MS 148, p.38r)

(5) We can only conjecture the cause, but we know the motive. (BB 15)

(6) There is no reddish green. (ROC II §16)

None of these sentences would be likely to be employed in a language class. Unlike (1), none of them defines or explains the meaning of a word in a way that would be useful to a learner. Rather, given the ordinary meanings of the words involved, these grammatical statements spell out some implications of the ways in which different concepts relate to each other. They are the results of “conceptual analysis” (ROC II §16); that is to say they are analytic truths.

To be sure, such statements or propositions are not what one might call “Frege‐analytic”: it is not possible by substituting synonyms for synonyms to transform any of them into a logical truth. But if we follow Wittgenstein in taking the meaning of a word to be its use in the language (PI §43), and if we note further that knowledge of the use of a word cannot be identified with knowledge of a synonymous expression (see Schroeder, 2006, ch.4.4) – we should not expect analyticity to boil down to Frege‐analyticity. In other words, if meaning comprises more than can be captured by paraphrase, we should not expect truth in virtue of meaning always to be susceptible of a formal proof by paraphrase.

Indeed, Wittgenstein’s examples of philosophically interesting grammatical statements can be described as analytic with even more propriety than a standard example of an analytic truth, such as (1). For they are obtained as a result of conceptual analysis, of a consideration of the meaning of words as manifest in their use, whereas (1) is not. That is because (1) serves as a grammatical rule. We actually learn that the word “bachelor” means “unmarried man.” This meaning must be clear to anyone understanding the word, hence – psychologically speaking – it is not something to be discovered by conceptual analysis.

Some of Wittgenstein’s remarks might be taken to contradict the idea that grammatical (or analytic) statements are true in virtue of the meanings of their ingredient words. Should we not rather say that grammatical statements are rules that constitute the meanings of the words in question? For instance, the rule “~ ~ p = p does not follow from the meaning of ‘not’ but constitutes it” (AWL 4; cf. PG 52). — Here, again, it is important to distinguish carefully between the relevant concepts. To recapitulate:

Grammatical norms govern the correct use, and hence the meanings of words. That a word is to be used in a certain way, that it is to be applied in this kind of case but not in that, is a grammatical norm. Yet for a grammatical norm to be operative, it need not be made explicit. It is possible that certain uses of a word are commonly accepted while others are rejected as false, a practice that is observed and emulated by learners, without any need for those norms ever to be formulated. Moreover, even where the meaning of a word is explained and not just picked up, the explanation may consist only in giving miscellaneous examples of correct applications as opposed to a rule.
Grammatical rules are general formulations of grammatical norms. Wittgenstein suggested that some grammatical norms (e.g., the meaning of the word “game”) can only be taught by examples, not by a general formulation (i.e., a definition). That may be disputed, but it is uncontroversial that most grammatical norms are, as a matter of fact, only taught by examples, not by general rules.
There are also formulations of implications of grammatical norms. From games we are familiar with the distinction between a rule and the implications of a rule. For example, it is not a rule of chess that in the position White: Ka1, Nb7; Black: Kh4 neither side can checkmate the other; but it follows from the rules. Although a logical implication of rules, it does not itself count as a rule because, first, it is too specific; secondly, somebody familiar with all the rules of chess need not be aware of it; and so thirdly, it cannot be invoked to settle a dispute (in the way in which you could cite a rule to explain why in a given position a certain move is impossible). Similarly, there is a distinction between grammatical norms (which may or may not be formulated as rules) and their implications, which we should not themselves regard as grammatical norms. For instance, if Wittgenstein is right, it is an implication of the grammatical norms that govern our use of sensation words that sensations are not inner objects (cf. (2) above). That that is not itself a grammatical norm is shown by the fact that it needs to be supported by philosophical argument and cannot be established simply by appeal to a competent speaker’s linguistic intuitions. A competent speaker, as someone who has mastered the grammatical norms of his language, should be able to recognize any infringement of a grammatical norm; but he need not therefore be aware of all the nontrivial implications of grammatical norms. Therefore he is not likely to discern immediately whether a philosophical thesis (such as Cartesian dualism) is indirectly in conflict with the norms of our grammar.
Both grammatical rules and the formulations of implications of grammatical norms are grammatical statements.

Now, grammatical norms are indeed constitutive of meaning, not derived from it. For meaning doesn’t exist independently of those norms. To say that a word has a certain meaning is to say that it is used according to certain semantic norms. However, the same is not true of a grammatical rule, a generalizing formulation of a norm. For the norm (and hence the meaning) could exist without being formulated as a rule.

For another reason, implications of norms cannot be said to constitute those norms. Of course there is no logical independence between the two (without that implication it would be a different norm), but there is a telling asymmetry: the norms were fixed and understood regardless of those implications, whereas those implications are derived from the norms. The norms can be invoked to justify the implications, but not vice versa, because the implications are not themselves recognized as norms.

Now regarding Wittgenstein’s claim that “~ ~ p = p does not follow from the meaning of ‘not’ but constitutes it” (AWL 4), we should, first of all, take him to mean the norm that is inherent in our use of the word “not,” rather than a formulation of that norm. Then we can agree that given our use of the word “not” to express simple negation, it does indeed not follow that double negation must be equivalent to a positive assertion (as was pointed out earlier, it could also be used to express emphatic negation). In other words, our use of double negation is not an implication of the norm that governs the straightforward uses of negation. Rather, it is something that needs to be specially determined, by a further norm.

6 Mathematics as Grammar

The key idea in Wittgenstein’s philosophy of mathematics is that mathematical propositions are not descriptions of timeless abstract entities, but norms of representation: rules of grammar. That explains their peculiar dignity: their certainty and necessity. The mathematical reliability and inexorability is ultimately our own reliability and inexorability in insisting on those rules and not allowing any exceptions to them.

There is a fairly uncontroversial sense in which some mathematical propositions can be called “rules”. For example, simple equations, such as in the times tables, which we memorize at an early age and apply when doing longer calculations. Thus, “3 × 9 = 27” is applied as a rule when working out the long multiplication: 399 × 39 (cf. PLP 53). Or, at a slightly more advanced level there are algebraic formulae that are both proven true and, afterward, memorized or consulted for repeated application, e.g., the cosine rule or the quadratic formula. — However, such cases are not what Wittgenstein has in mind when he calls mathematical propositions rules. “If one says the mathematical proposition is a rule,” he writes, “then of course not a rule in mathematics” (“Wenn man sagt, der mathematische Satz ist eine Regel, so natürlich nicht eine Regel in der Mathematik.”: MS 127, 236; post 4.3.44). Rather, on his view, mathematical propositions are rules of grammar, and, what is more, not the grammar of mathematical language, but the grammar of nonmathematical language. Thus, the equation “2 + 3 = 5” is a grammatical rule for the use of number words in a natural language, licensing, for instance, the inference from “I have two coins in my left pocket and three coins in my right pocket” to “I have five coins in my pockets” (cf. TLP 6.211).

Wittgenstein lays particular stress on the dependence of mathematics on its having applications outside mathematics (BT 566; RFM 257). That is what turns a mere calculus, a game of manipulating signs according to certain rules, into mathematics:

mathematical propositions containing a certain symbol are rules for the use of that symbol, and […] these symbols can then be used in non‐mathematical statements. (LFM 33)

However, if we now compare elementary mathematical propositions with ordinary grammatical rules – such as:

(1) A bachelor is an unmarried man.

— we find that they are significantly different. (1) expresses a norm that is constitutive of the meaning of its subject term: it explains what the word “bachelor” means. “Bachelor” and “unmarried man” are just two labels for the same concept. Hence, if you understand the expressions, you cannot ever know that one of them applies without knowing that the other one applies as well. By contrast, (as famously pointed out by Kant: Critique of Pure Reason, B 15) 7 + 5 and 12 are different concepts: they have different criteria of application (counting to 7 and counting to 5 versus counting to 12) (cf. RFM 357). Hence it is possible to count on a given occasion 7 objects and then 5 objects, but only 11 altogether (or, to use Wittgenstein’s example, 25 × 25, but not 625) (RFM 358e). In this case we have, initially, two distinct concepts, independently comprehensible – “Only through our arithmetic do they become one” (RFM 358; cf. 412, 432). Note the emphasis on “become”: if mathematical propositions are grammatical rules they are essentially additional ones: further rules for terms that are already understandable without them. Mathematical propositions are enriching existing meanings. The norm expressed by a grammatical proposition like (1), by contrast, does not change or enrich the meaning of the word “bachelor,” it gives it its meaning in the first place.

Hence, mathematical propositions would be more like the grammatical rule cited in the previous section, according to which double negation is equivalent to positive assertion, formalized as “~ ~ p ≡ p.” This rule does not determine the meaning of the negation sign from scratch. Rather, assuming an understanding of the meaning of the sign in single negation, it adds to it by giving a meaning to double negation.

Mathematical propositions can also be compared to a type of grammatical rule that is fairly common in scientific discourse. Sometimes what used to be an empirical discovery is later made part of a definition, for example, the velocity of light or the key properties of an acid. Thus, Wittgenstein writes with reference to mathematical propositions:

Every empirical proposition may serve as a rule if it is fixed, like a machine part, made immovable, so that now the whole representation turns around it and it becomes part of the coordinate system, independent of facts. (RFM 437)

For example, after first finding the concepts of 2 and 3 and of 5 empirically correlated, we come to introduce “2 + 3 = 5” as a mathematical proposition, that is: a norm of representation (RFM 51, 62, 324). If now the original experiment leads to a different result, we shan’t accept it: we shall insist that we must have made a mistake or that something strange must have happened to account for this deviation from our norm. And not only are elementary mathematical propositions based, genetically, upon corresponding empirical propositions, or experiences, they also require that our experiences continue to be, by and large, in agreement with our calculations. Although no individual experience can disprove an arithmetical equation, used as a norm of representation, a regular discrepancy between rule and experience would undermine the rule’s usefulness and eventually make us abandon or change it (RFM 51–2).

This is a central aspect of Wittgenstein’s account of mathematics that is well worth emphasizing. An equation, such as “2 + 2 = 4,” is not an empirical generalization, and hence no contrary experience can disprove it. On the other hand, it is not entirely independent of experience either. It is essentially a norm for describing countable things, like beans and sticks, and hence dependent on its suitability for the purpose (cf. RFM 357).

Elementary mathematical propositions have been grafted onto corresponding empirical observations. By contrast, it could never have been empirically discovered that a bachelor is an unmarried man. If elementary mathematical propositions are essentially additional rules for combining existing concepts, the question is whether these rules become fully integrated in our language, as Wittgenstein seems to suggest when he calls them “grammatical” or “instruments of language” (RFM 99, 162, 164–6, 358d, 359a). There are, I believe, reasons to return a negative answer: reasons not to regard mathematics – except perhaps for its very rudiments – as part of the grammar of our ordinary language.

First, what characterizes a grammatical norm is that, as it determines what makes sense, its negation, or a sentence that violates the norm it expresses, is nonsense. Yet that is not generally true of mathematical propositions. It may be so at the most elementary level. The sentence “I had two coffees in the morning and two in the afternoon, so I had only three overall today” is patently inconsistent. It might well be dismissed as not only false, but nonsensical. But suppose someone said:

(7) The pitch of the roof of my lean‐to garage is 15° to the horizontal and the roof extends 5.36 meter horizontally from the wall, and one side of the roof is 1.32 meter higher than the other.

We would hardly be inclined to dismiss that as nonsense, and yet a trigonometric calculation shows that:

(8) If a right‐angled triangle has an angle of 15° and the adjacent side is 5.36 then the opposite must be 1.44.

So (7) cannot be correct after all. And yet one can believe it to be correct – which speaks against regarding it as nonsense. For where there is no sense, there is nothing to believe.

Secondly, remember that according to Wittgenstein (at least in the realm of straightforwardly applicable mathematics) “the rule doesn’t express an empirical connection but we make it because there is an empirical connection” (LFM 292). The rule’s usefulness depends on its continued empirical appropriateness. It is not only that we reject (7) in the light of (8): that we insist that some of the measurements of the roof must have been inaccurate. It is also that when, in such a case, we measure or count again with greater care we shall almost certainly find our empirical observations in agreement with the rule (within the limits of accuracy achievable with our methods of measurement). In this case: if the other measurements prove reasonably accurate, we shall find that

(9) One side of the roof is indeed about 1.44 meter higher than the other side.

That is to say, according to Wittgenstein, we can take an empirical proposition, such as this, (9), as confirmation of a mathematical proposition, such as (8); confirmation not of the truth of (8) – for (8) is a rule, not a generalization – but confirmation of its suitability and usefulness in the light of experience. But to take (9) as an empirical proposition means to envisage the possibility of its being true or false; which means to envisage that something like (7) might have been true. So (7), although ruled out by a mathematical proposition (8), cannot be nonsense (as it would have to be if a mathematical proposition were not only a rule, but a grammatical rule: a norm for what makes sense in our language).

Still, in a broader sense of the word “grammatical,” we may accept mathematical propositions as grammatical rules, namely if we take the word to refer not to the grammar of our language, but only to a specific form of discourse, or, more generally, to a certain set of activities or of some institutionalized form of life. In a laconic remark in Philosophical Investigations Wittgenstein suggests that theology can be regarded as grammar (PI §373), providing rules for what can be said meaningfully about God. But these rules are binding only within a certain religious community. Thus, for a believer God is by definition omnipotent and benevolent. (And: “‘You can’t hear God speak to someone else, you can hear him only if you are being addressed’. – That is a grammatical remark.” [Z §717]) To question these attributes doesn’t make any sense within religious discourse: it would be “ridiculous or blasphemous” (AWL 32). And yet an agnostic or atheist may well do so. You can step outside religious language, flouting its grammatical norms, while remaining within language.

If we follow Wittgenstein in regarding mathematical propositions as grammatical rules, we need to understand the word “grammatical” in a similar way: not as determining what makes sense in a natural language, but rather fixing sense and nonsense in a specific kind of discourse or activity. That is, roughly speaking, an activity and discourse in which we try to develop and apply a system of calculating quantities, rather than simply counting or measuring them (cf. MS 117, p.138 f.).

References

Hacker, P.M.S. (1972/86). Insight and Illusion: Themes in the Philosophy of Wittgenstein. Revised edition. Oxford: Clarendon Press.
Schroeder, S. (2001). Elucidation and Ostensive Explanation. In G. Oliveri (Ed.). Wittgenstein Studies (Special Issue): From the “Tractatus” to the “Tractatus,” 69–79. Frankfurt: Peter Lang.
Schroeder, S. (2006). Wittgenstein: The Way out of the Fly‐bottle. Cambridge: Polity.