Glossary

(0, 2) compactification a generic heterotic string vacuum having d = 4, N = 1 supersymmetry. The world-sheet CFT has N = 2 right-moving superconformal invariance.

(2, 0) theory in current usage, this refers to a family of nontrivial fixed point theories with tensionless strings and d = 6 (2, 0) supersymmetry. These arise on coincident M5-branes and IIA NS5-branes, and on the IIB theory at an A–D–E singularity.

(2, 2) compactification one of a special subset of d = 4, N = 1 heterotic string vacua, which includes the Calabi–Yau compactifications. The world-sheet CFT has both right-moving and left-moving N = 2 superconformal invariance. In the type II string theories, these CFTs give vacua with d = 4, N = 2 supersymmetry.

A–D–E singularity a singularity of a four-(real)-dimensional complex manifold, resulting from the collapse of one or more two-spheres to zero volume. The terminology A–D–E refers to the Dynkin diagrams of the simply-laced Lie algebras, which describe the intersection numbers of the collapsed spheres.

Abelian differential a globally defined holomorphic (1,0)-form on a Riemann surface.

abstruse identity one of a set of quartic theta function identities due to Jacobi, it implies the degeneracy of bosons and fermions in GSO-projected string theories as required by supersymmetry.

affine Lie algebra see current algebra.

anomaly the violation of a classical symmetry by quantum effects. A gravitational anomaly is an anomaly in coordinate invariance. A global anomaly is an anomaly in a large symmetry transformation (one not continuously connected to the identity).

anomaly polynomial a formal (d + 2)-form in d-dimensions, which encodes the gauge and gravitational anomalies.

asymptotically locally Euclidean (ALE) space a space which at long distance approaches flat Euclidean space identified under a discrete group. This is the geometry in the neighborhood of an orbifold fixed point (or blown-up fixed point).

Atiyah–Drinfeld–Hitchin–Manin (ADHM) construction a method for the construction of all Yang–Mills field configurations having self-dual field strength.

auxiliary field a nonpropagating field, one whose field equation is algebraic rather than differential. In many supersymmetric theories, the transformations can be simplified by introducing such fields.

axion a Goldstone boson associated with spontaneously broken PQ symmetry. The model-independent axion appears in every perturbative string theory, and is closely related to the graviton and dilaton.

bc CFT a free CFT of anticommuting fields with an action of first order in derivatives. There is a family of such CFTs, parameterized by the weight h_b = 1 − h_c. For h_b = 2 this CFT describes the Faddeev–Popov ghosts associated with conformal invariance.

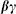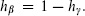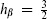CFT a free CFT of commuting fields with an action of first order in derivatives. There is a family of such CFTs, parameterized by the weight For this CFT describes the Faddeev–Popov ghosts associated with superconformal invariance.

Batalin–Vilkovisky formalism an extension of the BRST formalism, for quantizing more general theories with constraints. This has been useful in string field theory.

Becchi–Rouet–Stora–Tyutin (BRST) invariance a nilpotent symmetry of Faddeev–Popov gauge-fixed theories, which encodes the information contained in the original gauge symmetry.

Beltrami differential the derivative with respect to the moduli of the complex structure of a Riemann surface.

Berezin integration a linear operation taking functions of Grassmann variables to complex numbers, with many of the key properties of ordinary integration.

beta function 1. in quantum field theory, the derivative of the effective strength of an interaction with respect to length scale; 2. a special function involving a ratio of gamma functions, which appears in the Veneziano amplitude.

Betti numbers the number of nontrivial p-forms in de Rham cohomology, denoted B_p.

black hole entropy a quantity S proportional to the area of the horizon of a black hole, 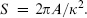This has the properties of a thermodynamic entropy: it is nondecreasing in classical general relativity, and the sum of the black hole entropy and the ordinary entropy is nondecreasing even with the inclusion of Hawking radiation. To find a statistical mechanical derivation of this entropy has been a major goal, partly realized in recent work.

black hole evaporation the emission of thermal (Hawking) radiation by a black hole, due to pair production near the horizon.

black hole information paradox a conflict between quantum mechanics and general relativity. Information falling into a black hole is lost and does not reappear when the black hole evaporates; this is inconsistent with ordinary quantum mechanical evolution. It apparently requires either a significant modification of quantum mechanics, or a significant breakdown of the usual understanding of locality.

black p-brane a p-dimensional extended object with an event horizon: a space that is translationally invariant in p directions and has a black hole geometry in the remaining directions.

blow up to deform a singular manifold into a smooth manifold.

Bogomolnyi–Prasad–Sommerfield (BPS) state a state that is invariant under a nontrivial subalgebra of the full supersymmetry algebra. Such states always carry conserved charges, and the supersymmetry algebra determines the mass of the state exactly in terms of its charges. BPS states lie in smaller supersymmetry representations than non-BPS states, so-called short representations. When there are short representations of different sizes, one also distinguishes ultrashort representations, which are the smallest possible (generally their dimension is the square root of the non-BPS dimension).

Borel summation a method of defining the sum of a divergent series. This has been used as a means of studying nonperturbative effects in field and string theories, but it should be understood that most nonperturbative effects are not usefully studied in terms of the perturbation series.

Born–Infeld action a generalization of the usual gauge field action which is nonpolynomial in the gauge field strength. This was originally proposed as a possible short-distance modification of electromagnetism. It arises as the low energy effective action of the gauge fields on D-branes.

bosonization the exact equivalence of a theory of fermionic fields and a theory of bosonic fields, possible in two dimensions. The boson is a fermion–antifermion pair; the fermion is a coherent state of bosons.

c-map a method for constructing the hypermultiplet moduli space of a type II string theory compactified on a Calabi–Yau three-fold from the vector multiplet moduli space of the other type II theory on the same three-fold.

c-theorem the existence, in unitary CFTs in two dimensions, of a positive quantity c that is monotonically nonincreasing with increasing length scale, and which at fixed points is stationary and equal to the central charge. This is a strong constraint on the global form of the renormalization group flow; no simple analog seems to exist in higher dimensions. Also known as the Zamolodchikov c-theorem.

CPT symmetry the combined operation of parity-reversal, time-reversal, and charge conjugation, which is a symmetry of all Lorentz-invariant local quantum field theories.

Calabi–Yau manifold a Kähler manifold with vanishing first Chern class. A Calabi–Yau n-fold has 2n real = n complex coordinates. Yau’s theorem guarantees the existence of a Ricci-flat metric of SU(n) holonomy.

canceled propagator argument a general principle implying, under broad conditions, the vanishing of surface terms on the moduli space of Riemann surfaces and therefore the decoupling of unphysical states in string amplitudes. Such amplitudes are defined by analytic continuation from a regime where the integrand falls rapidly at the boundary and the surface term is identically zero; its continuation is therefore also identically zero.

Casimir energy a shift in the ground state energy of a quantum field theory due to boundary conditions on the fields.

center-of-mass mode the zeroth spatial Fourier component of a quantum field.

central charge an operator (which might be a constant) that appears on the right-hand side of a Lie algebra and commutes with all operators in the algebra. Prominent examples include the constant term in the Virasoro algebra and the charges appearing on the right-hand sides of many supersymmetry algebras.

Chan–Paton degrees of freedom degrees of freedom localized at the endpoints of open strings. These are now interpreted as designating the D-brane on which the string ends.

Chan–Paton factor the vertex operator factor for the state of the Chan–Paton degrees of freedom.

Chern–Simons term a term in the action which involves p-form potentials as well as field strengths. Such a term is gauge-invariant as a consequence of the Bianchi identity and/or the modification of the p-form gauge transformation. These terms usually have a close connection to topology and to anomalies.

chiral 1. acting in a parity asymmetric fashion; see chiral multiplet, chiral symmetry, chiral theory, chirality, extended chiral algebra; 2. invariant under part of the supersymmetry algebra; see chiral field, chiral multiplet, chiral primary, chiral ring.

chiral field in supersymmetry, a local operator that is invariant under part of the algebra: the operator analog of a BPS state.

chiral multiplet the multiplet of d = 4, N = 1 supersymmetry with two real scalars. The quarks and leptons are contained in such multiplets. This multiplet is connected to both senses of chiral: it contains a fermion with chiral couplings, and the integral of the associated superfield is invariant under half of the supersymmetry algebra.

chiral primary in an N = 2 SCFT, a primary field that is also annihilated by one of the rigid supersymmetries .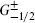

chiral ring the closed OPE algebra of chiral fields.

chiral symmetry a symmetry whose action on spinor fields is not parity-symmetric.

chiral theory a gauge theory in which the gauge couplings are not parity-symmetric.

chirality in d = 2k dimensions, the eigenvalue of the operator Γ^d which anti-commutes with the 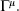This eigenvalue distinguishes the two Weyl representations, which are related to one another by parity.

Christoffel connection in general relativity, the connection that is constructed from the metric.

critical behavior the behavior of a quantum field theory at an IR fixed point with massless fields, and the approach to this behavior.

closed string a string with the topology of a circle.

cocycle in a vertex operator, an operator-valued phase factor which multiplies the creation–annihilation normal ordered exponential. This in needed in some cases in order to give the operator the correct commuting or anticommuting property.

coefficient functions the position-dependent coefficients of local operators appearing in the expansion of an operator product.

cohomology in any vector space with a nilpotent operator Q (one such that Q² = 0), the kernel of Q modulo the image of Q. That is, the space of closed states (those annihilated by Q) with the exact states (those of the form ) defined to be equivalent to zero. De Rham cohomology is the cohomology of the exterior derivative d acting on differential forms. On a complex manifold, Dolbeault cohomology is the cohomology of and (the (1, 0) and (0, 1) parts of d) on (p, q)-forms. Homology is the cohomology of the boundary operator. BRST cohomology is the cohomology of the BRST operator, and defines the physical space of a gauge-invariant theory.

Coleman–Weinberg formula the expression for the vacuum energy density of a free quantum field, from the renormalized sum of the zero-point energies of its modes.

collapsing cycle a cycle whose volume vanishes in a limit, usually giving rise to a singular manifold.

collective coordinate in quantizing a soliton or other extended object, the degrees of freedom corresponding to its position or configuration.

compact CFT a CFT in which the number of states with energy less than any given value is finite. This is defined by analogy with the spectrum of a differential operator on a compact space.

compactification scale the characteristic mass scale of states whose wavefunctions have a nontrivial dependence on the compact dimensions.

compactify to consider a field theory or string theory in a spacetime, some of whose spatial dimensions are compact.

complex manifold a manifold with an assigned system of complex coordinates, modulo holomorphic reparameterizations of these coordinates.

complex structure an equivalence class of complex coordinates. A given differentiable manifold may have many inequivalent complex structures.

complex structure moduli the moduli that parameterize the inequivalent complex structures on a manifold. In compactification on a Calabi–Yau 3-fold, these are associated with (2, 1)-forms.

conformal block in CFT, the contribution of a single conformal family to a sum over states.

conformal bootstrap the partially successful program to construct all CFTs by using only symmetry and consistency conditions.

conformal family the set of states obtained by acting on a highest weight state with Virasoro raising generators in all inequivalent ways; or, the corresponding set of local operators. A degenerate conformal family contains null states, which are orthogonal to all states in the family.

conformal field theory (CFT) a conformally invariant quantum field theory.

conformal gauge a choice of coordinates in two dimensions, such that the metric is proportional to the unit metric.

conformal Killing vector a globally defined infinitesimal diff×Weyl tranformation that that leaves the metric invariant.

conformal transformation a mapping of Euclidean or Minkowski space to itself that leaves the flat metric invariant up to a position-dependent rescaling; equivalently, the subgroup of diff × Weyl that leaves invariant the flat metric. In d ≥ 3 dimensions this has 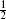(d + 1)(d + 2) parameters. In two dimensions it is the set of all holomorphic maps. Finite transformations require the inclusion of points at infinity, as in the case of the Möbius transformations of the sphere.
This usage has become standard in string theory and quantum field theory, but in general relativity conformal transformation is defined to be any position-dependent rescaling of the metric, now called a Weyl transformation in string theory.

conifold a Calabi–Yau manifold with a singular complex structure, corresponding to the collapse of a three-cycle. The string theory on this space is singular; this is now understood to be due to the quantum effects of a massless 3-brane wrapped on the cycle.

conifold transition a change of topology due to condensation of massless 3-brane fields. Under appropriate conditions, the potential for the massless 3-brane fields on a conifold with multiple collapsed cycles has a flat direction for these fields; this corresponds to a change of topology, blowing up a 2-cycle rather than the collapsed 3-cycle.

constraint a symmetry generator whose matrix elements are required to vanish in physical states, either in the BRST or OCQ sense. These can usually be understood as arising from a gauge symmetry (for so-called first class constraints, which are all that we consider), and consist of those gauge symmetry generators that do not vanish by the equations of motion.

coset CFT a CFT constructed as one of the factors of a known CFT, when the energy-momentum tensor of the latter can be written as a sum of commuting pieces. In the classic example the full CFT G is a current algebra, as is one of the factors (H). This can also be thought of as gauging the symmetry H.

cosmological constant the energy density of the vacuum. In a nonsupersymmetric quantum theory (including one with spontaneously broken supersymmetry), there are many effects that give rise to such an energy density. The cosmological constant problem is the problem that the cosmological constant in nature is many orders of magnitude smaller than known nonzero effects.

critical dimension the dimension in which a perturbative string theory is consistent in flat Minkowski spacetime; the value is 26 for the bosonic string and 10 for the supersymmetric string theories.

current algebra in quantum field theory, the algebra of the currents associated with a continuous symmetry group g (or of their Fourier modes). As used here, it is the specific algebra that occurs in two-dimensional CFTs, with the energy-momentum tensor defined to be of Sugawara form. The terms affine Lie algebra and affine Kac–Moody algebra are also used for this algebra, though like current algebra they both have broader definitions as well. The term affine refers to the c-number (Schwinger) term. An untwisted current algebra is the algebra of periodic currents, with integer modes. An algebra can be twisted by any automorphism of g.

cycle a topologically nontrivial submanifold (in the sense of homology); a p-cycle is p-dimensional. The A- and B-cycles are a standard basis for the nontrivial one-cycles on a Riemann surface.

D-brane in the type I, IIA, and IIB string theories, a dynamical object on which strings can end. The term is a contraction of Dirichlet brane. The coordinates of the attached strings satisfy Dirichlet boundary conditions in the directions normal to the brane and Neumann conditions in the directions tangent to the brane. A Dp-brane is p-dimensional, with p taking any even value in the IIA theory, any odd value in the IIB theory, and the values 1, 5, and 9 in the type I theory; a D9-brane fills space and so corresponds to an ordinary Neumann boundary condition. The Dp-brane is a source for the (p + 1)-form R–R gauge field. The mass or tension of a D-brane is intermediate between that of an ordinary quantum or a fundamental string and that of a soliton. The low energy fluctations of D-branes are described by supersymmetric gauge theory, which is non-Abelian for coincident branes.

D-instanton an object localized in (Euclidean) time as well as space, defined by Dirichlet conditions on all coordinates of attached strings. This is similar to a field-theoretic instanton, corresponding to a tunneling process that changes the value of an R–R field strength. More generally, the (p + 1)-dimensional world-volume of a Dp-brane, when localized in time and wrapped on a (p + 1)-cycle in space, has similar effects.

D-string a D1-brane, in the type I and IIB string theories.

D-term 1. in gauge theories with four or eight supersymmetries, the auxiliary field in the gauge multiplet; 2 the potential term proportional to the square of this auxiliary field, which depends only on the gauge couplings and, in the U(1) case, the value of the Fayet–Iliopoulos parameter.

Del Guidice–Di Vecchia–Fubini (DDF) operators operators satisfying an oscillator algebra, which create a complete set of physical states in OCQ.

descendant a state obtained by acting on a highest weight state with Virasoro raising generators.

diagonal modular invariant a modular-invariant CFT formed by imposing common boundary conditions on the left- and right-moving fields.

diff invariance general coordinate (reparameterization) invariance, usually applied to the world-sheet coordinates.

dilaton the massless scalar with gravitational-strength couplings, found in all perturbative string theories. An exactly massless dilaton would violate limits on nongravitational interactions, but a mass for the dilaton is not forbidden by any symmetry and so dynamical effects will generate one in vacua with broken supersymmetry (the same holds for other moduli). The string coupling constant is determined by the value of the dilaton field.

dimensional reduction in the simplest cases, toroidal compactification retaining only the states of zero compact momentum. More generally (and less physically) the construction of a lower-dimensional field theory by requiring all fields to be invariant under a set of symmetries; this may have no interpretation in terms of compactification.

Dirac quantization condition for an electric and a magnetic charge, the condition that the product be quantized, 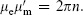For two dyons, which have both charges, the condition is 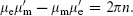These conditions generalize to objects of dimension p and d − p − 4 in d dimensions, where one is the source of a (p + 2)-form field strength and the other of the Poincaré dual (d − p + 2)-form field strength.

Dirac spinor the unique irreducible representation of the algebra of Dirac matrices, which is also known as a Clifford algebra. This is also a representation of the Lorentz group; in even dimensions it is reducible to two Weyl representations of the Lorentz group. The Dirac spinor is complex; in certain dimensions a further Majorana (reality) condition is compatible with Lorentz invariance.

Dirichlet boundary condition the condition that the value of a field be fixed at a boundary. This is the relevant usage in string theory, but in other contexts only the tangent derivative need be fixed.

discrete torsion in forming a twisted CFT, a change in the phases of the path integral sectors and therefore in the projection on the Hilbert space.

doubling trick the representation of holomorphic and antiholomorphic fields on a manifold with boundary by holomorphic fields alone, on the doubled copy of the manifold obtained by reflecting through the boundary.

dual resonance model a phenomenological model of the strong interaction, which developed into string theory. The dual refers here to world-sheet duality.

duality the equivalence of seemingly distinct physical systems. Such an equivalence often arises when a single quantum theory has distinct classical limits. One classic example is particle–wave duality, wherein a quantum field theory has one limit described by classical field theory and another described by classical particle mechanics. Another is the high-temperature–low-temperature duality of the Ising model. Here, low temperature is the statistical mechanical analog of the classical limit, the Boltzmann sum being dominated by the configurations of lowest energy. See Montonen–Olive duality, S-duality, string–string duality, T-duality, U-duality, world-sheet duality.

effective field theory the description of a physical system below a given energy scale (or equivalently, above a given length scale).

Einstein metric the metric whose leading low energy action is the Hilbert action

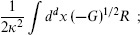
this is independent of other fields. Here is the gravitational coupling, related to the Planck length by 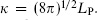This metric is related to other metrics such as the sigma-model metric by a field-dependent Weyl transformation. The existence of distinct metrics would appear to violate the equivalence principle, but when the dilaton and other moduli are massive the distinction disappears.

electroweak scale the mass scale of electroweak symmetry breaking, roughly 10² GeV.

enhanced gauge symmetry a gauge symmetry appearing at special points in moduli space, which is not evident in the original formulation of a theory. The classic examples are the gauge symmetries that arise at special radii of toroidal compactification, whose gauge bosons are winding states. Many other mechanisms are now known: D-branes and black p-branes wrapped on collapsing cycles, F-strings or D-strings stretched between various branes in the limit that the latter become coincident, and the gauge symmetry appearing on a zero size SO(32) instanton.

Euclidean having a metric of strictly positive signature. The original connotation that the metric be flat is somewhat disregarded; thus one refers to Euclidean quantum gravity, a conjectured analytic continuation of the Minkowskian theory. For the metric itself, the term Riemannian for a curved metric of Euclidean signature is more precise.

Euclidean adjoint in a Euclidean quantum theory, the Hermitean adjoint combined with time-reversal. The latter operation undoes the time-reversing effect of the adjoint, so that the combined operation is local.

Euler number the topological invariant

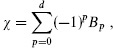
where B_p is the pth Betti number. It is equal to 2(1 − g) for a Riemann surface of genus g. More properly, the Euler characteristic.

expectation value a path integral with specified insertions. This is the term that we have chosen to use, but correlation function and correlator are also in common usage.

extended chiral algebra the full set of holomorphic operators in a CFT.

extended supersymmetry a supersymmetry algebra in which the supercharges comprise more than one copy of the smallest spinor representation for the given spacetime dimension.

F-term 1. the auxiliary field in the chiral multiplet of d = 4, N = 1 supersymmetry; 2. the potential term proportional to the square of this field.

F theory 1. a systematic description of IIB superstring states with nontrivial dilaton and R–R scalar backgrounds, which relates these fields to the modulus of an auxiliary two-torus; 2. a conjectured twelve-dimensional quantum theory underlying the IIB string. The name is inspired by M-theory, with F for father.

Faddeev–Popov determinant the Jacobian determinant arising from the reduction of a gauge-invariant functional integral to an integral over a gauge slice.

Faddeev–Popov ghosts the wrong-statistics quantum fields used to give a functional integral representation of the Faddeev–Popov determinant.

Fayet–Iliopoulos term in U(1) gauge theories with four or eight supersymmetries, a term in the action which is linear in the auxiliary D-term field.

Feigin–Fuchs representation a representation of minimal model expectation values in terms of free fields.

fibration a space which is locally the product of a fiber F and a base B. The geometry of the fiber varies as one moves over the base, and may become singular. Typical fibers are tori and the K3 manifold.

first Chern class on a complex manifold, the Dolbeault cohomology class of the Ricci form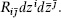

first-quantized description the representation of a quantized particle theory as a sum over particle paths, or of a string theory as a sum over world-sheets. Second-quantized refers to the representation in terms of a functional integral over ordinary or string fields. The term second-quantized implies the reinterpretation of the first-quantized wavefunction as a field operator. This terminology is in common usage, but it has been argued that it is unsatisfactory, in that it implies a deep principle where none may exist. Since the sum over world-sheets is itself a quantum field theory, one can equally well call it second-quantized, in which case string field theory is third-quantized. Third quantization of an ordinary field theory would describe operators that create and destroy universes, a concept which may or may not be useful.

Fischler–Susskind mechanism the cancellation of divergences and anomalies in the world-sheet quantum field theory against divergences and anomalies from integration over small topological features at higher orders of string perturbation theory. This is needed for the consistency of string perturbation theory in a quantum-corrected background.

fixed point 1. (in geometry) a point left invariant by a given symmetry transformation. This becomes a boundary point or a singularity if the space is identified under the transformation; 2. (in quantum field theory) a quantum theory whose physics is independent of length scale (scale-invariant). Usually such a theory is conformally invariant as well. A UV fixed point is the theory governing the short-distance physics of a quantum field theory; an IR fixed point is the theory governing the long-distance physics of a quantum field theory. A trivial IR fixed point has no massless fields. A nontrivial IR fixed point has massless fields with nonvanishing interactions. A theory whose IR limit is a massless free field theory is therefore described by neither of these terms; it is a noninteracting IR fixed point.

flat direction in scalar field space, a line of degenerate local minima. The field corresponding to this direction is a modulus.

flop a change of topology which can occur in weakly coupled string theory, where a two-cycle collapses and then a different two-cycle blows up.

fractional charge an unconfined particle whose electric charge is not a multiple of that of the electron. These exist in most d = 4 string theories, although in many cases all are superheavy.

fractional string theory a proposed generalization of string theory having constraints whose spin is not a multiple of . No complete construction exists.

Fuchsian group a discrete subgroup Γ of the SL(2, R) Möbius transformations of the complex upper-half-plane H, with additional conditions such that H/Γ is a manifold and in particular a Riemann surface.

functional integral in our usage, synonymous with path integral.

fundamental region in relation to a coset space M/Γ where Γ is a discrete group, a region F such that every point in M is identified with exactly one point in the interior of F or with one or more points on the boundary of F.

fundamental string (F-string) the original string whose quantization defines a weakly coupled string theory, as distinguished from D-strings and solitonic strings.

fusion rule the specification of which conformal families appear in the operator product of any two primary fields in a given CFT.

gauge-fixing the reduction of a redundant (gauge-invariant) description of a quantum theory to a description with a single representative from each equivalence class.

gaugino a spin- fermion in the same supersymmetry multiplet as a gauge boson.

gaugino condensation a strong coupling effect where a product of gaugino fields acquires a vacuum expectation value. This generally breaks a chiral symmetry but does not directly break supersymmetry; however, in combination with other fields it often induces supersymmetry breaking.

generation a family of quarks and leptons, described by spinor fields in a chiral but anomaly-free set of SU(3) × SU(2) × U(1) representations. In SU(5) grand unification these become a 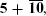in SO(10) they are contained in a 16, and in E₆ they are contained in a 27. An antigeneration is the conjugate representation; the distinction between generation and antigeneration is a matter of convention.

genus the number g of handles on a closed oriented Riemann surface: g = 0 is a sphere, g = 1 is a torus, and so on.

Gepner model a string model based on N = 2 minimal model CFTs.

ghosts see Faddeev–Popov ghosts.

Gliozzi–Scherk–Olive (GSO) projection a construction of modular-invariant string theories by summing over R and NS boundary conditions on the fermion fields and projecting onto states of definite world-sheet fermion number. In supersymmetric string theories there are independent GSO projections on the left-movers and right-movers. The diagonal projection, which acts simultaneously on both sides, produces a nonsupersymmetric theory.

goldstino the massless spin- Goldstone fermion associated with spontaneously broken supersymmetry. In supergravity it combines with the gravitino to form a massive fermion.

Goldstone boson the massless scalar corresponding to fluctuations of the direction of spontaneous symmetry breaking.

grand unification the unification of the SU(3)×SU(2)×U(1) gauge symmetries in a simple group.

grand unification scale the mass scale of spontaneous breaking of the grand unified group. Proton stability and the unification of the couplings require that it be within two or three orders of magnitude of the gravitational scale.

Grassmann variable the elements 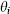of an algebra with the relation 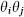= 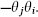These are used to give a path integral representation of fermionic fields, and to define superspace. They are also called anticommuting c-numbers.

gravitational scale the mass scale at which the dimensionless gravitational coupling becomes of order 1, m_grav = 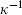= 2.4 × 10¹⁸ GeV; this is 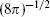times the Planck mass.

gravitino a spin-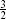 fermion in the same supersymmetry multiplet as the graviton.

Green–Schwarz mechanism the cancellation of an anomaly by the modified transformation law of a p-form potential in a Chern–Simons term.

Green–Schwarz superstring a manifestly supersymmetric formulation of the supersymmetric string theories, with a spacetime-fermionic gauge invariance known as symmetry. There is no simple covariant gauge fixing.

H-monopole a monopole carrying the magnetic charge of the antisymmetric tensor gauge field .

heterotic 5-brane the 5-brane carrying the magnetic charge of the massless heterotic string 2-form potential. It is obtained as the limit of a zero size instanton in the heterotic string gauge fields. The instanton configuration is localized in four spatial dimensions, and is therefore a 5-brane in nine spatial dimensions.

heterotic string a string with different constraint algebras acting on the left-and right-moving fields. The case of phenomenological interest has a (0, 1) superconformal constraint algebra, with spacetime supersymmetry acting only on the right-movers and with gauge group E₈ × E₈ or SO(32).

Hagedorn temperature the temperature at which the thermal partition function of free strings diverges, due to the exponential growth of the density of states of highly excited strings.

hidden sector the fields that couple to the Standard Model only through gravitational-strength interactions. In hidden sector models, these include the fields responsible for supersymmetry breaking.

highest weight state in CFT, a state annihilated by all Virasoro lowering operators, or more generally by all lowering operators in a given algebra.

Hodge number the number of nontrivial (p, q)-forms in Dolbeault cohomology, denoted h ^p,q.

holographic principle the conjecture that the states of quantum gravity in d dimensions have a natural description in terms of a (d − 1)-dimensional theory. This radical departure from local field theory was motivated by the black hole information problem, and has played a role in attempts to formulate M-theory.

holomorphic analytic, as used in the theory of complex variables. The Minkowskian continuation is left-moving. An antiholomorphic field is analytic in the conjugate variable, and its continuation is right-moving.

holomorphic quadratic differential a globally defined holomorphic (2, 0)-form on a Riemann surface.

holomorphic vector field a globally defined holomorphic (−1, 0)-form on a Riemann surface.

holonomy consider the parallel transport of a vector around a closed loop on a d-dimensional manifold: it returns to an O(n) rotation of its original value. The set of all rotations that are obtained in this way for a given manifold is a subgroup of O(n); this is the holonomy group.

homology see cohomology.

hyperelliptic surface a Riemann surface with a Z₂ symmetry. This can be represented as a two-sheeted cover of the sphere with branch cuts.

hyper-Kähler manifold a 4k-dimensional manifold of holonomy Sp(k) SO(4k). This is the geometry of the moduli space of hypermultiplets in d = 6, N = 1 or d = 4, N = 2 supersymmetry, in the limit in which gravity decouples.

hypermultiplet in d = 6, N = 1 or d = 4, N = 2 supersymmetry, the multiplet whose bosonic content is four real massless scalars.

identify to define two points (or other objects) to be equivalent, thus producing a coset space.

infrared (IR) divergence a divergence arising from long distances in spacetime, usually signifying that one has calculated the wrong thing.

inheritance principle in twisted (orbifold) theories, the principle that the tree-level amplitudes of untwisted states are the same as in the untwisted theory.

insertion the integrand of a path integral, excluding the weight exp(iS) or exp(−S).

instanton in a Euclidean path integral, a nonconstant configuration that is a local but not a global minimum of the action. Such configurations are usually localized in spacetime, are usually topologically nontrivial, and are of interest when they give rise to effects such as tunneling that are not obtained from small fluctuations around a constant configuration. Spacetime instantons are instantons in the effective field theory in spacetime. World-sheet instantons are instantons in the world-sheet quantum field theory, and correspond to world-sheets wrapping around nontrivial two-cycles of spacetime.

intersection number the number of points at which a set of surfaces intersect, weighted by the orientation of the intersection.

irrelevant interaction an interaction whose dimensionless strength decreases with increasing length scale. In perturbation theory, this is equivalent to a non-renormalizable interaction.

K3 manifold the unique nontrivial Calabi–Yau manifold of four (real) dimensions. To be precise, it is topologically unique, but possesses complex structure and Kähler moduli. Its holonomy is SU(2), so that half of the supersymmetries of a theory are broken upon compactification on K3.

Kac determinant the determinant of the matrix of inner products of states at a given L₀ level of a Verma module.

Kac–Moody algebra see current algebra.

Kähler form the (1, 1)-form 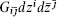, formed from a Kähler metric on a complex manifold.

Kähler manifold a complex manifold of U(n) holonomy in n complex dimensions.

Kähler moduli the moduli parameterizing the Kähler form.

Kähler potential the potential K(z, ), in terms of which the metric of a Kähler manifold is determined, 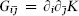. This is not globally defined, being determined only up to a Kahler transformation K(z, ) → K(z, ) + f(z) + f(z).

Kaluza–Klein gauge field in a compactified theory, a gauge field originating from the metric of the higher-dimensional theory. The gauge group is the isometry group of the compact space.

Kaluza–Klein monopole a monopole carrying the magnetic charge of a U(1) Kaluza–Klein gauge symmetry. The monopole configuration is the smooth Taub–NUT spacetime. It is localized in three spatial dimensions, and is therefore a 6-brane in nine spatial dimensions.

Kaluza–Klein states states with nonzero momentum in a compact spatial direction.

Knizhnik–Zamolodchikov (KZ) equation the differential equation determining the expectation values of the primary fields of a current algebra.

Landau–Ginzburg model a scalar field theory which has a nontrivial IR fixed point when the potential is appropriately tuned. In particular, this gives a Lagrangian representation of the minimal model CFTs.

large coordinate transformation a coordinate transformation that is not continuously connected to the identity.

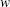
lattice the set Γ of integer linear combinations of n linearly independent basis vectors in n dimensions. Given a Euclidean or Lorentzian metric, an even lattice is one whose points have even length-squared. The dual lattice Γ is the set of points such that · 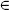Z for all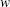 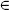Γ. The root lattice is the set of integer linear combinations of the roots of a Lie algebra.

level 1. the quantized c-number term in a current algebra, also known as the Schwinger term; 2. the total oscillator excitation number in free field theory; 3. in a conformal family, the difference between the L₀ eigenvalue of a given state and that of the highest weight state.

level-matching the modular invariance condition that 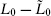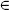Z.

Lie algebra an algebra with an antisymmetric product that satisfies the Jacobi identity. A simple Lie algebra has no subalgebra that commutes with its complement. A simply-laced Lie algebra has all roots of equal length. A graded Lie algebra has odd and even elements, with a symmetric product between odd elements.

light-cone gauge in string theory, the choice of world-sheet time coordinate to coincide with a particular spacetime null coordinate. In theories with local symmetries, a gauge choice such that the connection in a given null direction vanishes.

linear dilaton theory a scalar CFT in which the energy-momentum tensor includes a term proportional to the second derivative of the scalar. This arises in string theory when the dilaton is a linear function of position.

linear sigma model a scalar field theory whose kinetic term is field independent, but whose long-distance physics is governed by a nonlinear sigma model.

Liouville field theory the CFT of a scalar field with an exponential interaction. This arises in various situations, including the noncritical string. It corresponds to bosonic string theory in a linear dilaton plus exponential tachyon background.

little string theory one of several interacting string theories without gravity, notably found on NS5-branes in the limit of zero string coupling.

loop expansion in quantum field theory, the Feynman graph expansion, which is equivalent to the expansion in powers of 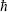. The string loop expansion is the sum over Riemann surfaces, with dimensionless string coupling g. The world-sheet loop expansion is the nonlinear sigma model perturbation expansion, in powers of with R_c the compactification radius.

Lorentzian having a mixed signature (−, . . . ,−,+, . . . , +).

lowering operator operators that reduce the energy of a given state. In CFT, operators that reduce the Virasoro generator L₀ (or 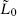) by n units carry a grading (subscript) n.

M-theory 1. (narrow) the limit of strongly coupled IIA theory with eleven-dimensional Poincaré invariance; 2. (broad; most common usage) the entire quantum theory whose limits include the various weakly coupled string theories as well as M-theory in the narrow sense. The name is deliberately ambiguous, reflecting the unknown nature of the theory; M has variously been suggested to stand for membrane, matrix, mother, and mystery.

M2-brane the 2-brane of M-theory, which couples to the potential A₃ of eleven-dimensional supergravity.

M5-brane the 5-brane of M-theory, which carries the magnetic charge of the potential A₃ of eleven-dimensional supergravity.

macroscopic string a string whose length is much greater than the characteristic string length scale. In particular, it is sometimes useful to consider an infinite string stretching across spacetime.

Majorana condition a Lorentz-invariant reality condition on a spinor field. This can be imposed only if the spacetime dimension is 1, 2, 3, 4, or 8 (mod 8).

marginal interaction an interaction whose dimensionless strength is independent of the length scale. In general this might hold only to first order in the coupling of the interaction; a truly marginal interaction is one that remains marginal even with finite coupling.

matrix models quantum mechanical systems with matrix degrees of freedom, with critical points governed by noncritical string theories.

matrix theory a quantum mechanical system with matrix degrees of freedom and 32 supercharges, obtained by dimensional reduction of d = 10 super-symmetric U(n) Yang–Mills theory. In the large-n limit this is conjectured to define M-theory (in the broad sense).

minimal models several families of solvable CFTs, in which every conformal family is degenerate. There are infinite series of unitary minimal models having N = 0, N = 1, and N = 2 superconformal symmetries, which converge from below on the central charges 1, 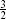, and 3 respectively.

Minkowskian having a signature (−, +, +, . . . , +).

mirror symmetry an equivalence between string theories compactified on distinct manifolds. The equivalence reverses the sign of the U(1) charge of one N = 2 superconformal algebra, and therefore changes the sign of the Euler number of the manifold.

Möbius group the globally defined SL(2, C) conformal symmetry of the sphere; or, the globally defined SL(2, R) conformal symmetry of the disk.

mode operators the spatial Fourier components of a quantum field.

model see vacuum.

modular group the group of large coordinate transformations (often applied to a Riemann surface but also applicable to spacetime).

modular invariance the invariance of the string path integral under large coordinate transformations.

moduli 1. the parameters labeling the geometry of a manifold. Notable examples are the parameters for the complex structure of the string world-sheet, and the parameters for the geometry of compactification; 2. the parameters labeling a space of degenerate (and, usually, physically inequivalent) vacua in quantum field theory. This is closely related to the compactification example: in expanding around the classical limit, each compact solution of the field equations gives a vacuum of the quantum theory, to leading order; 3. the massless fields corresponding to position dependence of these parameters. Contrast Goldstone boson.

moduli space the space of geometries or vacua, whose coordinates are the moduli.

monodromy for a quantity which is locally single-valued, the multi-valuedness around nontrivial closed paths.

Montonen–Olive duality the weak–strong duality of d = 4, N = 4 Yang–Mills theory.

Nambu–Goto action a string action, which is proportional to the invariant area of the world-sheet in spacetime.

Narain compactification the abstract description of toroidal compactification in terms of the lattice of left- and right-moving momenta.

naturalness problem the problem of explaining why a constant of nature takes a value much smaller than estimated nonzero contributions. Examples are the Higgs scalar mass, the cosmological constant, and the QCD 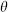-angle.

Neumann boundary condition the condition that the normal derivative of a field vanish at a boundary; the value of the field is free to fluctuate.

Neveu–Schwarz algebra the world-sheet algebra of the Fourier modes of the supercurrent and energy-momentum tensor, in a sector where the supercurrent is antiperiodic and its moding therefore half-integer-valued.

Neveu–Schwarz (NS) boundary condition the condition that a fermionic field on the world-sheet be antiperiodic, in the closed string or in the double of the open string (see doubling trick). Its Fourier moding is then half-integer-valued.

Neveu–Schwarz 5-brane in the type I and type II superstring theories, the 5-brane that carries the magnetic charge of the NS–NS 2-form potential.

Neveu–Schwarz–Neveu–Schwarz (NS–NS) states in type II superstring theories, the bosonic closed string states whose left- and right-moving parts are bosonic. These include the graviton and dilaton, and in the type II case a 2-form potential.

no-ghost theorem 1. the theorem that the OCQ or BRST Hilbert space has a positive inner product; 2. the further theorem that the string amplitudes are well defined and unitary in this space.

no-scale model a field theory that has, to some approximation, a line of degenerate vacua with broken supersymmetry.

Noether’s theorem the theorem that an invariance of the Lagrangian implies a conserved quantity.

noncommutative geometry a generalization of ordinary geometry, focusing on the algebra of functions on a space. The noncommutative collective coordinates of D-branes suggest the need for such a generalization.

noncritical string theory 1. a Weyl-noninvariant string theory — one with a measure of world-sheet distance that is independent of the embedding in spacetime. These include strings with an independent world-sheet metric field, and strings with a short-distance cutoff; 2. more recently, the term has been applied to any string theory that does not have a weakly coupled limit with a Weyl-invariant world-sheet theory. In this form it includes various theories with stringlike excitations in which the coupling is fixed to be of order 1, such as the (2,0) theory and the little string theories. Such a theory does not have a well-defined world-sheet, because processes that change the world-sheet topology cannot be turned off.

nonlinear sigma model a scalar field theory in which the kinetic term has a field-dependent coefficient. This has a natural interpretation in terms of a curved field space, and corresponds to string theory in curved spacetime, or more generally one with position-dependent background fields.

nonrenormalization theorem a theorem restricting the form of quantum corrections to a given amplitude, or to the effective action. It may require that these corrections vanish, that they arise only at specific orders of perturbation theory, or that they arise only nonperturbatively.

normal ordering a prescription for defining products of free fields by specific subtractions of divergent terms. Conformal normal ordering, denoted : :, produces operators with simple conformal properties. Creation–annihilation normal ordering, denoted 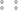, where lowering operators are put to the right of raising operators, produces operators with simple matrix elements. Boundary normal ordering, denoted , is conformal normal ordering with an additional image charge subtraction to produce operators that are finite as they approach a boundary.

null state a physical state that is orthogonal to all physical states including itself. Or, a descendant in a conformal family which is orthogonal to all states in the family.

old covariant quantization (OCQ) a method of quantizing string theory, similar to the Gupta–Bleuler quantization of electrodynamics. It is equivalent to the light-cone and BRST quantizations.

one-loop the leading quantum correction, coming from surfaces of Euler number zero in string perturbation theory.

open string a string that is topologically a line segment.

operator equation in quantum theory, an equality between operators that holds in arbitrary matrix elements; equivalently, an equality that holds when inserted into a functional integral with arbitrary boundary conditions.

operator product expansion (OPE) the expansion of a product of operators as a sum of local operators. This provides an asymptotic expansion, as the separation of the operators vanishes, for an arbitrary expectation value containing the product. In CFT the expansion is convergent.

orbifold 1. (noun) a coset space M/H, where H is a group of discrete symmetries of a manifold M. The coset is singular at the fixed points of H; 2. (noun) the CFT or string theory produced by the gauging of a discrete world-sheet symmetry group H. If the elements of H are spacetime symmetries, the result is a theory of strings propagating on the coset space M/H. A non-Abelian orbifold is one whose point group is non-Abelian. An asymmetric orbifold is one where H does not have a spacetime interpretation and which in general acts differently on the right-movers and left-movers of the string; 3. (verb) to produce such a CFT or string theory by gauging H; this is synonymous with the third definition of twist.

oriented string theory a string theory in which the world-sheet has a definite orientation; world-sheet parity-reversal is not treated as a gauge symmetry.

orientifold a string theory produced by the gauging of a world-sheet symmetry group H, where H includes elements that combine the world-sheet parity-reversal with other symmetries.

orientifold plane a plane (of any dimension p) consisting of fixed points of the orientifold group H (specifically, of an element of H that includes ).

p-brane a p-dimensional spatially extended object. Examples are black p-branes, Dp-branes, M2- and M5-branes, NS5-branes, heterotic 5-branes, and (in d > 4) Kaluza–Klein monopoles.

p-form a fully antisymmetric p-index tensor, usually written in an index-free notation.

p-form gauge field a generalization of Abelian gauge theory, with a p-form potential A, a (p − 1)-form gauge parameter 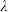, and a (p + 1)-form field strength F. For p = 0 this is an ordinary massless scalar; for p = 1 it is an Abelian gauge field. A (p+1)-form potential couples naturally to a p-brane, through the integral of the form over the world-volume. A self-dual p-form theory is one where F = F; this requires the spacetime dimension to be d = 2p + 2, and further d must be 2 mod 4 (in the Minkowskian case) in order that = 1.

p-p′ string an open string with one endpoint on a Dp-brane and the other on a Dp′-brane.

(p, q)-form on a complex manifold, a tensor that is completely antisymmetric in p holomorphic indices and q antiholomorphic indices.

(p, q) string a bound state of p F-strings and q D-strings in the IIB theory.

parafermion CFT a family of coset CFTs with Z_n symmetry, generalizing the Z₂-invariant free fermion theory. These describe the generic critical behavior of a system with Z_n symmetry.

parity transformation an operation that reflects one spatial dimension, or any odd number. One distinguishes spacetime parity, P (or 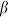) and world-sheet parity .

partition function a sum over the spectrum of a quantum system, weighted by e^−H/T where H is the Hamiltonian and T the temperature. Often additional charges are included in the exponent. This is the basic object in equilibrium statistical mechanics. In string theory it is given by a path integral on the torus or the cylinder, and so arises in one-loop amplitudes.

path integral a representation of the transition amplitudes of a quantum system as a coherent sum over all possible histories. In quantum mechanics the history is a particle path; in quantum field theory it is a path in field space; in first-quantized string theory it is the embedding of the string world-sheet in spacetime.

Pauli–Villars regulator a means of regulating quantum field theories by introducing a very massive wrong-statistics field.

Peccei–Quinn (PQ) symmetry an approximate symmetry, violated only by anomalies.

period matrix a g × g matrix characterizing the complex structure of a genus-g Riemann surface.

perturbation theory the expansion of the amplitudes of a quantum system in powers of the coupling.

physical state in a quantum system with constraints, a state annihilated by the constraints. In OCQ this is a state annihilated by the Virasoro lowering generators and having a specified L₀ eigenvalue.. In BRST quantization it is a state annihilated by the BRST operator. In both these cases, the true physical spectrum is the space of physical states with an additional equivalence relation, physical states differing by a null state being identified.

picture in the RNS superstring, one of several isomorphic representations of the vertex operators. The q-picture consists of vertex operators of 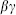ghost charge q. The natural pictures are q = − 1 and −, with higher pictures including partial integrations over supermoduli space. The picture changing operator increases q by one.

Planck length the natural length scale of quantum gravity, L_P = 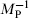= 1.6 × 10⁻³³ cm, constructed from 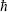, c, and G_N.

Planck mass the natural mass scale of quantum gravity, M_P = 1.22×10¹⁹ GeV, constructed from 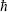, c, and G_N.

plumbing fixture a procedure for constructing higher genus Riemann surfaces from lower ones by sewing in a handle. The construction includes a parameter q, such that when q goes to 0 the handle degenerates or pinches. This gives a canonical representation of the boundary of the moduli space of Riemann surfaces.

Poincaré dual a map from p-forms to (d − p)-forms, given by contraction with the completely antisymmetric tensor.

Poincaré invariance the invariance group of the flat metric, consisting of translations and Lorentz transformations.

point group the orbifold group H, with translations ignored (applicable only for orbifolds having a spacetime interpretation).

Polyakov path integral a representation of first-quantized string theory as a path integral with an independent world-sheet metric. A local Weyl symmetry guarantees that the classical degrees of freedom are the same as those of the Nambu–Goto theory.

primary field in CFT, a local operator annihilated by all of the lowering generators of a given algebra, such as the Virasoro algebra. The corresponding state is a highest weight state.

projective space a compact n-dimensional space constructed from a linear (n + 1)-dimensional space by identifying points under the overall rescaling (₁, . . . , x_n+1) (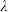x₁, . . . , 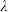x_n+1). For _i and 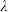real this produces RPⁿ, and for _i and 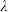complex it produces CPⁿ (which has n complex = 2n real dimensions).

pseudospin in a current algebra, an SU(2) subalgebra not contained in the Lie algebra of the center-of-mass modes.

puncture a marked point on a Riemann surface, the position of a vertex operator.

QCD string a reformulation of non-Abelian gauge theory as a string theory, conjectured to exist at least in the limit of a large number of colors.

quaternionic manifold a 4k-dimensional manifold with the holonomy group Sp(k) × SU(2) SO(4k), with specific SU(2) curvature. This is the geometry of the moduli space of hypermultiplets in d = 6, N = 1 or d = 4, N = 2 supergravity.

R symmetry a symmetry that acts nontrivially on the supercurrent(s).

raising operator operators that reduce the energy of a given state. In CFT, operators that increase the Virasoro generator L₀ (or 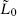) by n units carry a grading (subscript) −n.

Ramond algebra the world-sheet algebra of the Fourier modes of the supercurrent and energy-momentum tensor, in a sector where the supercurrent is periodic and its moding therefore integer-valued.

Ramond (R) boundary condition the condition that a fermionic field on the world-sheet be periodic, in the closed string or in the double of the open string (see doubling trick). Its Fourier moding is then integer-valued.

Ramond–Neveu–Schwarz (RNS) superstring the formulation of type I and II superstrings that has superconformal invariance but not manifest spacetime supersymmetry. The latter emerges after imposing the GSO projection on the string Hilbert space.

Ramond–Ramond (R–R) states in type I and type II superstring theories, the bosonic closed string states whose left- and right-moving parts are fermionic. These include p-form potentials C_p, with p taking all odd values in the IIA string and all even values in the IIB string.

rank 1. the maximal number of commuting generators of a Lie algebra; 2. the number of indices on a tensor.

rational CFT a CFT with a finite number of primary fields under an extended chiral algebra, a generalization of the minimal models. Such CFTs are highly constrained.

refermionization after bosonization, the construction of new spin- fields from linear combinations of the bosonic fields. These fermions are nonlocal, nonlinear functions of the original fermions.

Regge behavior in scattering at large center-of-mass energy-squared s and fixed momentum transfer-squared −t, the scaling of the amplitude as s^(t). The values of t where (t) = j is a nonnegative integer correspond to exchange of a particle of spin j and mass-squared −t.

Regge slope denoted ′, the square of the characteristic length scale of perturbative string theory. The tension of the fundamental string is .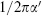

relevant interaction an interaction whose dimensionless strength increases with distance. In perturbation theory, this is equivalent to a superrenormalizable interaction.

renormalization group equation the differential equation governing the change of physics with length scale.

renormalization theory the calculus of path integrals.

Riemann–Roch theorem the theorem that the number of metric moduli minus the number of conformal Killing vectors on a Riemann surface is −3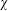, with 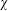being the Euler number of the surface; and, generalizations of this result.

Riemann surface a two-(real)-dimensional complex manifold, equivalent to a Weyl equivalence class of Riemannian manifolds.

root a vector of the eigenvalues of the maximal set of commuting generators of a Lie algebra, associated with a state in the adjoint representation.

S-duality a duality under which the coupling constant of a quantum theory changes nontrivially, including the case of weak–strong duality. Important examples are the SL(2, Z) self-dualities of IIB string theory and of d = 4, N = 4 supersymmetric Yang–Mills theory. More loosely, it is used for weak–strong dualities between different theories, such as IIA–M-theory (on a circle) duality, SO(32) heterotic–type I duality, and E₈ heterotic–M-theory (on an interval) duality. In compactified theories, the term S-duality is limited to those dualities that leave the radii invariant, up to an overall coupling-dependent rescaling; contrast T-duality and U-duality.

S-matrix the overlap amplitude between states in the infinite past and states in the infinite future; the scattering amplitude. In coordinate-invariant quantum theories this is generally the simplest invariant. The term usually implies a basis of free particle states; this is problematic in theories with massless particles due to IR divergences, and meaningless in theories at nontrivial IR fixed points.

scale transformation a rigid rescaling of spacetime, or of the world-sheet.

Scherk–Schwarz mechanism the breaking of supersymmetry by dimensional reduction that includes a spacetime rotation.

Schottky group a discrete subgroup Γ of the SL(2, C) Möbius transformations of the sphere S₂, with additional conditions such that S₂/Γ is a manifold and in particular a Riemann surface.

Schwarzian the combination of derivatives appearing in the finite conformal transformation of the energy-momentum tensor.

Schwinger–Dyson equation the operator equations of a quantum theory, expressed as equations for the expectation values.

short multiplet see BPS state.

sigma model metric the metric appearing in the string world-sheet action. Also known as the string metric, this differs from the Einstein metric by a dilaton-dependent Weyl transformation.

simple current an operator J such that, for any primary field 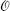, the operator product J 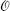contains only a single conformal family.

soliton a state whose classical limit is a smooth, localized, and (usually) topologically nontrivial classical field configuration; this includes particle states, which are localized in all directions, as well as extended objects. By contrast, a state of ordinary quanta is represented near the classical limit by small fluctuations around a constant configuration. In a theory with multiple classical limits (dualities), solitons and quanta may exchange roles.

special Kähler geometry the geometry of the moduli space of vector multiplets in d = 4, N = 2 supergravity. It is most simply defined (section B.7) in terms of special coordinates, which are fixed up to a symplectic transformation. Rigid special geometry is obtained in the limit where gravity decouples and the supersymmetry becomes global.

spectral flow the adiabatic change in the spectrum produced by a continuous change in the boundary conditions.

spin the behavior of a field or a state under rotations. In a CFT this is given in terms of the conformal weights by h − .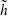

spin field the vertex operator for a Ramond ground state, which produces a branch cut in the spinor fields.

spin structure one of a set of inequivalent ways of defining a spinor field globally on a manifold. Roughly speaking, it corresponds to a choice of signs in the square roots of the transition functions.

spurious state in OCQ, a state produced by Virasoro raising operators.

state–operator isomorphism in CFT, a one-to-one isomorphism between states of the theory quantized on a circle and local operators. Also, a one-to-one isomorphism between states of the theory quantized on an interval and local operators on a boundary. In d dimensions the circle becomes a (d − 1)-sphere and the interval a (d − 1)-hemisphere.

string coupling the dimensionless parameter g governing the weights of different Riemann surfaces in string perturbation theory, the contribution from surfaces of Euler number 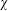being weighted by g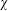⁻. The string coupling is related to the dilaton by g = e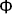. This definition corresponds to the amplitude to emit a closed string; the amplitude to emit an open string is proportional to g^1/2.

string field theory the representation of string theory as theory of fields, the fields being maps from a circle (or interval) into spacetime. This corresponds to an infinite number of ordinary quantum fields. This formalism can reproduce string perturbation theory, but it is unclear whether it can be defined beyond perturbation theory.

string metric see sigma model metric.

string scale the mass scale 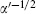characterizing the tower of string excitations.

string–string duality a term sometimes used to denote a weak–strong duality between different string theories, in particular between the heterotic string compactified on T⁴ and the IIA string compactified on K3.

string tension the mass per unit length of a string at rest, related to the Regge slope by .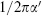

Sugawara construction in current algebra, the construction of the energy-momentum tensor as a product of two currents. Originally proposed as a phenomenological model in four dimensions, this was later found to be an exact result in two dimensions.

superconformal algebra an extension of the conformal (Virasoro) algebra to include anticommuting spinor generators. The (N, ) superconformal algebra has N left-moving and right-moving supercurrents.

superconformal current algebra an extension of the conformal transformations to include both spin-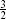 and spin-1 currents.

superconformal field theory (SCFT) a quantum field theory that is invariant under superconformal transformations.

supercurrent a conserved spinor current. This includes the world-sheet current T_F associated with superconformal transformations, and the spacetime current associated with spacetime supersymmetry.

superfield a field on superspace, with specific transformation properties under a change of coordinates.

supergravity the union of general relativity and supersymmetry, implying also the promotion of supersymmetry to a local symmetry.

supermanifold (or superspace) a formal extension of the concept of manifold to include both commuting and anticommuting (Grassmann) coordinates.

supermoduli the anticommuting parameters characterizing a super-Riemann surface.

superpartner scale the mass scale of the superpartners of the Standard Model particles. This is expected to be between 10² and 10³ GeV if supersymmetry solves the naturalness problem of the Higgs scalar mass.

superpotential in d = 4, N = 1 supersymmetry, the holomorphic function of the superfields that determines the nongauge interactions.

super-Riemann surface a supermanifold defined in terms of superconformal transition functions between patches.

supersymmetry a symmetry whose charge transforms as a spinor, which relates the masses and couplings of fermions and bosons.

supersymmetry breaking scale the mass scale of the expectation value that breaks supersymmetry. The superpartner scale is the supersymmetry breaking scale times the strength of the coupling of the Standard Model fields to the supersymmetry breaking fields.

T-duality a duality in string theory, usually in a toroidally compactified theory, that leaves the coupling constant invariant up to a radius-dependent rescaling and therefore holds at each order of string perturbation theory. Most notable is R → 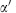/R duality, which relates string theories compactified on large and small tori by interchanging winding and Kaluza–Klein states. More generally it includes shifts of antisymmetric tensor backgrounds and large coordinate transformations in spacetime. Contrast S-duality and U-duality.

’t Hooft–Polyakov monopole a classical solution with magnetic charge, which exists whenever a simple group is spontaneously broken to a group with a U(1) factor.

tachyon a particle (almost always a scalar) with a negative mass-squared, signifying an instability of the vacuum.

tadpole an amplitude for creation of a single particle from the vacuum, induced by quantum effects.

target space the space in which a function takes its values. This is usually applied to the nonlinear sigma model on the string world-sheet, where the target space is itself spacetime.

Teichmüller parameters the moduli for the complex structure of a Riemann surface (strictly speaking, points in Teichmller space are not identified under the modular group).

tensionless string theory an interacting theory with tensionless strings. These can arise as p-branes with p − 1 directions wrapped on a collapsing cycle, as various 2-branes with one direction stretched between higher-dimensional branes when the latter become coincident, and on zero-size E₈ × E₈ instantons. In general the coupling is fixed to be of order one, so there is no perturbation expansion. Tensionless implies that the string tension in units of the gravitational scale goes to zero; it is not applied to the fundamental string, which becomes noninteracting in that limit.

tensor multiplet 1. the multiplet of d = 6, (1, 0) supersymmetry whose bosonic content is one self-dual tensor and one scalar. This reduces to a vector multiplet of d = 4, N = 2 supersymmetry; 2. the multiplet of d = 6, (2, 0) supersymmetry whose bosonic content is one self-dual tensor and five scalars. This reduces to a vector multiplet of d = 4, N = 4 supersymmetry.

tensor operator in CFT, a local operator whose conformal or superconformal transformation involves only the first derivative of the transformation; synonymous with a primary field of the conformal or superconformal symmetry. Such an operator is mapped to a highest weight state by the state–operator isomorphism.

tetrad a basis of d orthonormal vector fields in d dimensions. The term tetrad originates in d = 4 (as does the equivalent term vierbein) but there is no other convenient term for general d.

the theory formerly known as strings see M-theory, second definition.

theory see vacuum.

theta functions the family of holomorphic functions having simple periodicity properties on a torus.

Thirring model the solvable quantum field theory of a single Dirac fermion with a quartic interaction in 1 + 1 dimensions. This is equivalent under bosonization to a free scalar field at a general real radius.

threshold correction a correction to the low energy effective action, and in particular to the gauge coupling, due to virtual massive particles.

topological string theory a modification of string theory without local dynamics; all observables are topological.

toric geometry a generalization of the idea of projective space. Roughly speaking, this corresponds to the most general linear sigma model.

toroidal compactification the periodic identification of one or more flat dimensions.

torsion a term applied to various 3-form field strengths, so called because they appear in covariant derivatives in combination with the Christoffel connection.

tree-level the Feynman graphs which become disconnected if one propagator is cut, or the analogous string amplitudes, the sphere and disk. These correspond to classical terms in the effective action.

twist 1. (verb) to define a field in a periodic space to be aperiodic by a symmetry transformation h; 2. (noun) the aperiodicity h; 3. (verb) given a CFT or string theory, to construct a new theory using a symmetry group H. One adds closed strings twisted by any of the elements h 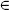H, and requires all states to be invariant under the transformations in H. This is equivalent to treating H as a world-sheet gauge symmetry. The term orbifold is also used as a synonym; 4. (noun, archaic) world-sheet parity.

twisted state a closed string with twisted periodicity.

type ... supergravity the low energy supergravity theory of the corresponding string theory. The Roman numeral signifies the number of d = 10 supersymmetries, and IIA and IIB distinguish whether the two supersymmetries have opposite or identical chiralities respectively.

type I superstring the theory of open and closed unoriented superstrings, which is consistent only for the gauge group SO(32). The right-movers and left-movers, being related by the open string boundary condition, transform under the same spacetime supersymmetry.

type IIA superstring a theory of closed oriented superstrings. The right-movers and left-movers transform under separate spacetime supersymmetries, which have opposite chiralities.

type IIB superstring a theory of closed oriented superstrings. The right-movers and left-movers transform under separate spacetime supersymmetries, which have the same chirality.

type 0 string a pair of nonsupersymmetric string theories, which have tachyons and no spacetime fermions, with the same world-sheet action as the type II theories but with different projections on the Hilbert space.

U-duality any of the dualities of a string theory, usually of a toroidally compactified type II theory. This includes the S-dualities and T-dualities, but in contrast to these includes also transformations that mix the radii and couplings.

ultrashort multiplet see BPS state.

unit gauge a choice of coordinate and Weyl gauges in two dimensions, such that the metric is the identity.

unitary as applied to a quantum system, the property of having a conserved inner product in a positive-norm Hilbert space.

unoriented string theory a string theory in which world-sheet parity-reversal is a discrete gauge symmetry. The perturbation theory includes unoriented world-sheets, and the spectrum is restricted to states with = +1.

UV divergence a divergence arising from short distances in spacetime, usually signifying a limit to the validity of a theory.

vacuum a stable Poincaré-invariant state. The novel feature of systems with unbroken supersymmetries is the frequent appearance of degenerate but physically inequivalent vacua.
While it is now clear that the different string theories are actually different vacua in a single theory, it is still common to use the term theory for each. Also, different CFTs within a single string theory are sometimes referred to as different theories rather than vacua. The term model is used to refer to string vacua whose low energy physics resembles the Standard Model.

vector multiplet in d = 4, N = 1 or d = 6, N = 1 supersymmetry, the multiplet whose bosonic content is a massless vector field. The d = 6 multiplet reduces to a vector field plus two real scalars in d = 4, N = 2 supersymmetry.

Veneziano amplitude the bosonic string tree-level amplitude for four open string tachyons.

Verma module the set of states obtained by acting on a highest weight state with Virasoro raising generators in all inequivalent ways, with the requirement that all such states be linearly independent (the generators act freely). This gives a representation of the Virasoro algebra that depends on the central charge c and on the weight h of the highest weight state. This is very similar to a conformal family, except that in the case of a degenerate representation some states in the latter may vanish; the Verma module would in this case give a reducible representation.

vertex operator a local operator on the string world-sheet, corresponding to a string in the initial or final state.

Virasoro algebra in a CFT, the infinite-dimensional Lie algebra of the Fourier modes of the energy-momentum tensor.

Virasoro–Shapiro amplitude the bosonic string tree-level amplitude for four closed string tachyons.

W algebras a family of extended chiral algebras with currents of spin greater than 2.

W string a proposed generalization of string theory with constraints of spin greater than 2. No complete construction exists.

Ward identity a relation between the divergence of the expectation value of a conserved current and the same expectation value without the current.

weight 1. in CFT, the L₀ or 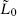eigenvalue, which determines the behavior of an operator under scale transformations and rotations (= conformal weight); 2. in Lie algebra, a vector of the eigenvalues of the maximal set of commuting generators of a Lie algebra, in a state of a given representation.

Wess–Zumino consistency condition the condition that the second derivative of a functional integral with respect to the background fields be symmetric. This strongly constrains the form of possible anomalies in a theory.

Wess–Zumino–Novikov–Witten (WZNW) model a conformally invariant nonlinear sigma model on a group manifold with an antisymmetric tensor background.

Weyl anomaly an anomaly in the Weyl transformation, this determines the critical dimension in the Polyakov formalism. This is sometimes called the trace anomaly or the conformal anomaly.

Weyl condition in even dimensions, the condition that a fermion have definite chirality. This defines a spinor representation of the Lorentz group, which contains half of the components of the Dirac representation of the gamma matrix algebra.

Weyl transformation a position-dependent rescaling of the metric.

Wilson line 1. a gauge field with vanishing field strength but with nontrivial parallel transport (holonomy) around nontrivial paths in spacetime. 2. the gauge-invariant operator that measures such a field: the trace of the path-ordered product of the line integral of the vector potential.

Wilsonian action the action in a low energy effective field theory, which incorporates the effects of higher energy virtual states.

winding state a closed string whose configuration is a nontrivial path in a non-simply-connected spacetime.

world-sheet 1. the two-dimensional surface in spacetime swept out by the motion of a string. 2. the abstract two-dimensional parameter space used to describe the motion of a string.

world-sheet duality the equivalence between Hamiltonian descriptions obtained by cutting open a string world-sheet along inequivalent circles. Important examples are the associativity condition, from the four-point sphere amplitude, and the equivalence of the open string loop and closed string tree descriptions of the cylinder.

wrapped refers to a p-brane, q of whose dimensions are wound on a nontrivial compact submanifold of spacetime, leaving a (p − q)-dimensional extended object.

Yang–Mills field non-Abelian gauge field.

Zamolodchikov metric the expectation value of a pair of local operators on the sphere, giving a natural inner product for the corresponding string states. This is the metric that appears in the kinetic term in the spacetime action.

zero modes 1. of a differential operator: eigenfunctions with zero eigenvalue. In a Gaussian functional integral, these would give an infinite factor in the bosonic case and a zero factor in the fermionic case. In general these have a physical origin and the functional integral has an appropriate integrand to give a finite result; 2. center-of-mass modes.

zero-point energy the energy due to vacuum fluctuations of quantum fields.

zero-slope limit the limit → 0. Only massless string states, described by low energy field theory, remain.