| 7 | Markets with Black Swans |
| Graciela Chichilnisky |
Black Swans are rare but catastrophic events. They are famously difficult to assess using standard measures of risk (Posner, 2004), and arise from financial innovation that causes widespread volatility and default (Chichilnisky and Wu, 2006). It is well known that market behavior focuses on short term and immediate risks, and seldom considers system-wide risks that are infrequent but potentially catastrophic. These are Black Swans and impact the economy as a whole. An ongoing puzzle is whether it is possible to benefit from market trading and innovation without the risk of Black Swans.
This chapter shows how a classic method to measure and manage risks introduced in the first part of the last century by Von Neumann and Morgenstern, and subsequently adopted by all major economists since the 1950 to price securities such as stocks and bonds, makes the economy insensitive to catastrophic events. An axiom introduced by Von Neumann and Morgenstern led to the use of expected utility optimization, a criterion that typically ignores rare events (Chichilnisky, 1996, 2000, 2009a, 2011). This was followed by similar axioms of decision theory — all of them equivalent — introduced by Arrow (1971), who called it “Monotone Continuity”; Hernstein and Milnor (1953), who called it “Continuity”; and DeGroot (2004), who called it A-4. In its various forms the axiom became a standard feature in the theory of markets under uncertainty, leading to the criterion of “expected utility optimization.” In its simplest form, as we show in this article, Von Neumann–Morgenstern’s axiom creates a systematic bias against, or insensitive behavior towards, events that are rare but potentially catastrophic (Chichilnisky, 1996a,b, 2000, 2002). The problem is quite general, and it appears in all sorts of markets, with either bounded or unbounded state spaces, and includes markets with infinitely many states of nature, described for example by real numbers, where the existence of market equilibrium reflects expected utility optimization that neglects, as shown in Chichilnisky (2000), catastrophic events or Black Swans.1
It is unquestionable that the global economy is vulnerable to catastrophic risks. Black Swans are rare but catastrophic events that are modifying our views. Rezai, Foley, and Taylor (2012) study a growing economy with climate change, which is a potentially catastrophic risk. A global carbon market created to deal with the risk of climate change as part of the United Nations Kyoto Protocol, is now international law and trading US$200 Bn/year (Chichilnisky and Sheeran, 2009). The Great Depression is another type of Black Swan. Another is the global financial crisis that started in 2007 after a period of intense financial innovation as predicted in Chichilnisky and Wu (2006). In 2009, at the height of the global financial crisis, a newly created global institution, the G-20, broadcast a Leaders’ Statement about the need for “sustainable development” alerting the world about potential catastrophic risks.2
This chapter establishes the economic foundations for markets with Black Swans, how to successfully manage risks and attain efficient market solutions when facing rare but potentially catastrophic events. The results are new in several ways. First, we define a new concept of a market with Black Swans, a significant extension of Arrow–Debreu markets to encompass rare but catastrophic events that are beyond the standard theory of markets, Chichilnisky (1996a,b,c,d, 1998, 1999, 2000, 2002, 2006, 2009a,b,c, 2010a,b, 2011, 2012). Secondly, we show how standard decision theory based on Von Neumann Morgenstern axioms fails in these markets, and how to improve upon this situation by defining a new type of preference — sustainable preferences — that are sensitive to rare as well as to frequent events. These preferences represent more realistically the way traders perceive Black Swans and how to manage risks in situations involving catastrophic events, and were introduced in Chichilnisky (2000, 2009c, 2012). Finally we show the interconnection of traders’s decisions and the consistency of our definitions by providing a single condition — limited arbitrage — and showing that it is necessary and sufficient for the existence of an efficient market equilibrium in markets with Black Swans.
As defined by the G-20 (see note 1) sustainability means that the economy must live within its means — both financial and ecological — and can continue into the future avoiding catastrophes.3 A natural question is whether unchecked profit making in a market economy conspires against sustainability or, reciprocally, whether a society that is committed to sustainability must in some way restrain or even discard markets. This would be a major challenge, since markets are today a widespread form of organization. This chapter argues that it is possible to reconcile markets and sustainability, but it requires markets to be sensitive to rare events. Equivalently, it requires that traders have “sustainable preferences” as introduced in Chichilnisky (1996a,b, 2000, 2002). These new preferences lead to new ways to evaluate financial assets such as shares and bonds. Since markets follow the traders’ priorities, when traders have sustainable preferences markets become sustainable: sustainable decisions are made and financial instruments are priced accordingly. Financial innovation is possible under certain conditions. Limited diversity of the traders restrains their willingness to inflict widespread risks of default on the economy as a whole, because it checks the size of the trades they are willing to entertain. This self-limiting process is the essence of the limited arbitrage condition introduced in Chichilnisky (1991, 1994a,b 1996e,f, 1997) and, in a nutshell, explains the existence results of the chapter. Whether markets clash with sustainability hinges therefore on whether traders have sustainable preferences, and on whether the economy as a whole has limited arbitrage.
Sustainable preferences are based on new axioms for decision theory that require equal treatment of the frequent and rare events such as Black Swans, see Chichilnisky (1996a,b). They reflect an increasing body of empirical evidence about how humans value widespread risks (Chichilnisky, 1996a,b). Based on the concept of sustainable preferences, this chapter defines markets with Black Swans, which differ from standard Arrow–Debreu markets, in two ways: (i) traders have sustainable preferences and (ii) traders engage in short trades. Markets with sustainable preferences overcome rare but realistic risks of widespread volatility and default because they are neither focused on frequent nor on rare events; they are in fact sensitive to both, as required for sustainable development. Market prices take a new role: they represent the value of consumption under current uncertainty as well as the value of consumption in a Black Swan event. This approach resolves the conflict between a market’s short-term objectives and the goals of sustainability, without eliminating market organization. We show also that these markets exhibit a suitable ambiguity — as would be expected in an economy with rare events — which we show in our last section to be connected with the “uncertainty principle” and the “incompleteness” results of Godel.
We establish the existence of equilibrium by showing that, when traders have sustainable preferences, a single condition — limited arbitrage (Chichilnisky, 1991, 1993, 1994a,b, 1996e,f) — is necessary and sufficient for the existence of Pareto efficient market equilibrium, without requiring bounds on short sales. To achieve this, we have to overcome three interlinked technical issues that require a careful use of topology and continuity: (i) continuity of preferences and prices, (ii) compactness of trading sets and efficient allocations, both of which (i and ii) are used to prove existence of solutions, and (iii) appropriate supporting prices for efficient allocations.4 We adopt the “sup norm” topology that allows a uniform treatment among all generations, a topology that was already used for the same purpose in T. Koopmans’s classic work (Koopmans, 1960, 1972).
This section defines sustainable markets, see Chichilnisky (1996g, 1997a,b, 2012a,b).
A competitive market has H ≥ 2 traders and N ≥ 2 commodities that are traded over various states of nature t ∈ R+. The consumption of commodities yields utility u(x(t)) at each state t, where x(t) ∈ RN, and u(x): RN → R+ is a concave increasing real valued function that represents instantaneous utility in state t. Following the classic work of Debreu (1953), and Chichilnisky (1996a,b, 2009a,b), one can view consumption over states of nature (x(t)t∈R+) as elements of L∞(RN), with a standard Lebesgue measure μ. Similarly, utility defined over various states of nature f(t) = u(x(t)) are elements of the linear space L∞(R), where L∞ is the space of all essentially bounded measurable real valued functions on R with the sup norm || f ||= ess supt∈R |f(t)| . In this context a preference over uncertainty U : L∞ → R is a real valued linear function ranking utility paths u(x(t)), while U : L∞ (RN) → R denotes the ranking of consumption paths (x(t)), which is based on a concave instantaneous utility u : RN → R, and is generally non-linear. We say that the preference over uncertainty U is insensitive to rare events when it disregards utility in events of small enough probability, namely U(f) > U(g) ⇔ U(f′) > U(g′) for any a.e. (almost anywhere) modification of f and g that occurs on sets of small measure, namely when f′(t) = f(t) and g′(t) = g(t) for all t ∉ S, where μ(S) < ε. Similarly a ranking is insensitive to frequent events when it disregards utility modifications on sets of large measure, formally, for any two paths f, g, there exists an N(f,g) ∈ R : U(f) > U(g) ⇔ U(f′) > U(g′) for any a.e. modification of f, g that occurs on sets of measure at least N(f,g), namely whenever f′(t) = f(t) and g′(t) = g(t) for all t ∈ S with μ(S) > N(f,g). The logical negation of these two insensitivity properties defines sensitivity to rare and frequent events, respectively. In the former case we say that preference is sensitive to Black Swans.
A sustainable preference U is an increasing ranking that (as a state dependent preference) satisfies three axioms.5
Axiom 1.U : L∞ → R is continuous and linear6
Axiom 2.U : L∞ → R is sensitive to frequent events
Axiom 3.U : L∞ → R is sensitive to Black Swans
These axioms were introduced in Chichilnisky (1996a,b). The first two are consistent with Von Neumann’s classic axioms of choice over uncertainty and are satisfied by expected utility, for example
U(f) = U(x(t)) = ∫R+ u(x(t))e−δtdμ, δ > 1
where f ∈ L∞ represents a time path u(x(t)), δ is an uncertainty “discount factor.” Observe that the expected utility U(f) defined above is linear on utility paths u(t), and thus satisfies Axiom 1, but it may not be linear in consumption x. Sustainable preferences that satisfy Axioms 1, 2, and 3 are also linear on utility paths but may not be linear on consumption. The third axiom, however, is not satisfied by expected utilities (Chichilnisky, 1996a,b). All sustainable preferences have been characterized in a representation theorem established in Chichilnisky (1996a,b, 2009a,b, 2010a,b) to be of the form
|
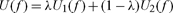(1) |
where U1(.) is a function in L1 and U2(.) is in L∞* − L1, 0 < λ < 1, both U1(f) and U2(f) are increasing and non-zero, and specifically:
U(f) = U(x(t)) = λ ∫R+ u(x)Φ(x)dμ + (1 − λ)χ(u(x))
where U1(f) = λ ∫R+ u(x) ø(x)dt, U2(f) = (1 − λ)χ(u(x), 0 < λ < 1, Φ ∈ L1, e.g. (t) = e−δt, and χ ∈ L∞* −L1 is a purely finitely additive measure on R that gives measure to “Black Swan” events (for a proof, see Chichilnisky (1996a,b, 2009a,b, 2010a,b)).
Definition: A market with Black Swans is an Arrow–Debreu market without bounds on short sales, and where traders have sustainable preferences that are sensitive to rare events
A sustainable market economy can be represented as E = [X, Ωh, Uh, : X → R,h = 1,…H}. It has H ≥ 2 traders indexed by h = 1,2, …, H, N ≥ 2 commodities that are traded over uncertainty t ∈ R+; the consumption space or trading space is the Banach space X = L∞ with the sup norm || · ||sup (Debreu, 1953), Chichilnisky (1996a,b, 2009a,b); this assumption implies no bounds on short sales. Ωh,∈ X represents trader h′s property rights, Ω = Σh Ωh represents society’s total resources over time; and traders’ preferences over uncertainty Uh : L∞ → R+ are based as above on concave instantaneous utility uh: RN → R+ and define sustainable preferences over uncertainty.
Traders may have zero endowments of some goods, and endowments could be negative or positive; since the trading space is X = L∞, short selling is allowed. We consider general preferences where the normalized gradients to indifference surfaces define either an open or a closed map on every indifference surface, namely (i) indifference surfaces contain no half-lines, for example strictly convex preferences, or (ii) the normalized gradients to any closed set of indifferent vectors define a closed set, for example linear preferences. In this chapter for simplicity we identify case (ii) with linear preferences. The assumptions and the results of the chapter are ordinal, and Uh(0) = 0 and supx∈X Uh (x)= ∞. Preferences are increasing so that Uh(x(t)) > Uh(y(t)) when for all t, x(t) ≥ y(t) and for a set of positive Lebesgue measure, x(t) > y(t). In addition, we assume the traders’ preferences are uniformly non-satiated, which means that they can be represented by a utility U with a bounded rate of increase: for smooth preferences, which are Frechet differentiable, ∃ε, K > 0 :∀x ∈ X, K > || DU(x) || > ε. If a utility function is uniformly non-satiated, its indifference surfaces are within a uniform distance from each other: ∀r, s∈ R, ∃N(r, s) ∈ R such that f ∈ U−1 (r) ⇒ ∃y ∈ U−1(s) with || f − g || ≤ N(r, s), see Chichilnisky and Heal (1998a,b).
Assumption 1: Each trader has a sustainable preference that is represented by an increasing, uniformly non-satiated function of consumption over uncertainty U: L∞ → R+ based on a concave instantaneous utility u: RN → R such that U(0) = 0 and supf ∈X U(f) = ∞.
Prices are real valued linear functions on X that are continuous with the sup norm (Debreu, 1953). The space of feasible allocations over uncertainty is {(f1(t),…,fH(t)) ∈XH : ∑h=1Hfh(t) = ∑h=1H Ωh = Ω}. To simplify notation when it is clear we obviate the state variable t. A utility vector U = (U1(f1)… UH(fH)) is feasible if the allocation (f1,…,fH) is feasible.
The set of individually rational feasible allocations is the set of utility allocations {U1(f1)… UH(fH)} that are feasible and preferred to the initial endowments, ∀h, Uh(fh) ≥ Uh(Ωh). A utility vector U = (U1(f1),…, UH(fH)) — which need not be feasible — is efficient or undominated if there is no allocation G = (g1 gH) such that ∀h, Uh(gh) ≥ Uh(fh) and Uk(gk) > Uk(fk) for some k, and there exists a sequence of feasible allocations (f1j,…,fHj)j=1,2,… such that G = limj→∞ (f1j,…,fHj)j=1,2,…. A feasible efficient allocation is a feasible allocation that is also efficient.
The Pareto frontier P(E) ⊂ R+H is the set of individually rational and efficient feasible utility vectors. A competitive equilibrium of the economy E consists of a price vector p* ∈ X*+ and an allocation (f1*,…,fH*) ∈ XH such that fh* optimizes Uh over the budget set Bh(p*) = {f∈ X: 〈p*,f〉 = 〈p*, Ωh} and clears the markets ∑h=1Hf*h − Ωh = 0. A feasible allocation (f1,…,fH) is a quasi-equilibrium when there is a price p ≠ 0 with ∀h, 〈p, Ωh〉 = 〈p,fh〉, and 〈p,g〉 ≥ 〈p,fh〉 for any g implies Uh(g) ≥ Uh(fh). A quasi-equilibrium is a competitive equilibrium when Uh(g) > Uh(fh) ⇒ 〈p,g〉 > 〈P,fh〉.
The following concept of a global cone contains global information about a trader since, in ordinal terms, the sequences in this cone achieve utility values that eventually exceed those of all trades. The global cone was introduced in Chichilnisky (1991, 1993, 1994a,b, 1996e,f), see also Chichilnisky and Heal (1998a,b).
Definition: The cone Ah consists of all sequences of net trades {fj} in X along which the hth trader’s utility increases and exceeds that of any other vector in the space; it can be based on rays of directions in X along which the hth trader’s utility exceeds eventually all utility values:
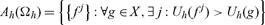
Definition: The global cone Gh(Ωh) is the set of all sequences of net trades in X along which the hth trader’s utility never ceases to increase; it can be based on rays of directions with ever increasing utility:
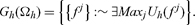
We assume that Gh(Ωh) has a simple structure, which was established in different forms in Chichilnisky (1991, 1994b, 1998), Chichilnisky and Heal (1998): when preferences have no half-lines in their indifferences, case (i), then Gh(Ωh) is the closure of Ah(Ωh), and in case (ii) when preferences have half-lines in their indifference surfaces, for example linear preferences, then Gh(Ωh) = Ah(Ωh).
Definition The market cone Dh(Ωh) is
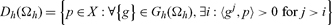
This is the set of all prices assigning eventually strictly positive value to net trades in the global cone. We assume the results of the following proposition, which was established in different forms in Chichilnisky (1991, 1994a,b, 1995, 1996c,d, 1998), Chichilnisky and Heal (1998), and is used in proving the connection between limited arbitrage and the existence of a sustainable market equilibrium:
Proposition 1: If a utility U : X → R is uniformly non-satiated, then
(A) A(Ω) ≠ Ø, and the cones G(Ω) and D(Ω), are all convex and uniform across vectors Ω in X.7 For general preferences G(Ω) and D(Ω) may not be uniform, Chichilnisky (1998), Chichilnisky and Heal (1998)
(B) In case (i), preferences have no half-lines in their indifferences, 
; with linear preferences case (ii) Gh = Ah.
This section defines limited arbitrage and provides an intuitive interpretation in terms of gains from trade in markets with Black Swans. The following definitions and results are used in establishing the existence of a competitive equilibrium and extend Chichilnisky (1991, 1994a, 1996c,d, 1998), Chichilnisky and Heal (1998), and Chichilnisky (2011, 2012a) to markets with Black Swans.
Definition: Gains from trade are defined as
Definition: The economy E satisfies limited arbitrage when
 |
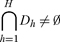(2) |
Geometrically, limited arbitrage (2) bounds arbitrage opportunities in the economy by limiting the utility that can be achieved by the traders when trading with each other. Under the assumptions, Proposition 2 below applies in case (i) and (ii): either indifference surfaces contain no half-lines (e.g. strictly convex preferences) of (ii) linear preferences.
Proposition 2: In markets with Black Swans limited arbitrage implies bounded gains from trade, namely G(E) < ∞.
Proof: The proof relies on limited arbitrage, and follows the proofs of similar propositions in Chichilnisky (1991, 1998) and Chichilnisky and Heal (1998) adapted to markets with sustainable preferences. Along the way we also highlight properties of sustainable preferences that are useful for understanding the structure of sustainable preferences, and the existence of a competitive equilibrium in sustainable markets.
Assume E has limited arbitrage and without loss of generality that ∀h, Ωh = 0. For every h, let Uh = U1h + U2h, where U1h and U2h are the two (non-zero) parts of the sustainable preference Uh that exist according to the representation of sustainable preferences provided in (1) above, see Chichilnisky (1996a,b). If gains from trade G(E) were not bounded there would be a sequence of feasible, individually rational allocations of increasing utility {gj} = {g1j,…, gHj}j=1,2… satisfying (i)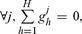 
, (ii) ∀h,j Uh(ghj+1 ) > Uh(ghj) and (iii) for some k, limj→∞(Uk(gkj)) = ∞, which implies that limj→∞ || gkj ||∞ = ∞. Define the set of traders K by k ∈ K ⇔ limj→∞ Uk(gkj) = ∞ so that in particular limj || gkj || = ∞; then by assumption 
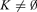We show that limited arbitrage contradicts (i); (ii) and (iii) so that gains from trade G(E) cannot be unbounded with limited arbitrage. By definition of limited arbitrage (2) for j > j0 there exists a p and a j0 such that Σh∈K 〈p, ghj〉 > 0 for j >j0, because (ii), (iii) imply that ∀ h, {ghj} is in Gh(0). However, by (i) 
so that ∀p > 0, Σh∈J〈p, ghj〉= 0, a contradiction. The contraction arises from assuming that G(E) is not bounded. Therefore, limited arbitrage implies bounded gains from trade, as we wanted to show.
Next, we derive properties of general sustainable preferences, as stated above. Observe that, under limited arbitrage, when the sequence of purely finitely additive utilities {U2h(ghj)} in (2) grows without bound as j → ∞, so does the countably additive sequence {U1h(ghj)}j→∞ in (2). Assume, to the contrary, that {U2h(ghj)} grows without bound but {U1h(ghj)} is bounded. Since as we saw above gains from trade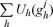 
are bounded under limited arbitrage, for each h, {Uh(ghj)}j is bounded. However, for each j, U2hj = Uhj − U1hj and the right-hand side is bounded by assumption, because Ujh is bounded and we just assumed U1hj to be bounded as well. Therefore, the sequence {U2h (ghj)}j must be bounded, which is a contradiction. Therefore, under the conditions, when the sequence of purely finitely additive utilities {U2h (ghj)}j→∞ grows without bound so does the countably additive sequence of utilities{U1h (ghj)}. For each h consider the sequence of normalized vectors (ghj/ || ghj ||), denoted also {ghj}. We now show that the sequence of normalized vectors {ghj} has a weak* limit, and that its weak limit is not zero. First observe that the normalized sequence {ghj} is contained in the unit sphere of L∞, which is weak* compact by Alaoglu’s theorem. Consider a subsequence with a weak* limit; we show that this weak limit is not zero. Since X = L∞ and utilities are continuous and sustainable, the preferred sets have non-empty interiors and by the properties of sustainable preferences presented above there exist two non-zero prices p1 ∈ L1 and p2 ∈ L∞* − L1,8 such that p1 supports the preferred set of U1h, at {0}, denoted U1h0, and p2 supports the preferred set of U2h at {0} denoted U2h0, so that p = p1 + p2 supports the preferred set of Uh at {0}, Uh0. We saw that, under limited arbitrage and with sustainable preferences, for any h, limj U2h(ghj) = ∞ implies that lim j→∞ U1h(ghj) = ∞, namely when purely finitely additive utility values grow without bound, the corresponding countably additive parts do too. This implies in turn that ∀h, when the limiting utility values limj Uh(ghj) = limj(U1h(ghj) + U2h(ghj)) = ∞, then limj→∞ U1h(ghj) = ∞, since limj Uh(ghj) = ∞ and Uhj(ghj) = U1h(ghj) + U2h(ghj) implies that either limj→∞ U1h(ghj) = ∞ as we wish to prove, or else limj→∞ U2h(ghj) = ∞, which in turn implies that limj→∞ U1h(ghj) = ∞ as seen above. Thus in all cases limj Uh(ghj) → ∞ implies limj→∞ U1h(ghj) = ∞ as we wished to prove. Next observe that for all h there exist a subsequence denoted also {ghj}, j0 and r > 0, such that 〈p1, ghj〉 ≥ r when j >j0. Otherwise, limj 〈p1, ghj〉 = 0 and in particular for any t > 0, and ε >0, ∃j: U1h(ghj) > t and (p1, ghj) < ε. But ∀y satisfying 〈p1,y〉 < 0, U1h(y) < U1h0 because p1 supports U1h0. Therefore by continuity limj U1h(ghj) ≤ 0, a contradiction since we showed that limj→∞ U1h(ghj) = ∞. Therefore
 |
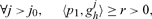(3) |
which implies that the sequence {ghj} is weak* bounded away from zero, by definition, since p1 ∈ L1. Therefore we have shown that the weak* compact sequence {ghj} contains a subsequence, denoted also {ghj}, with a weak* limit denoted gh, which is not zero because of (3). Consider now the cone C defined by all strictly positive convex combinations of the vectors gh for all h. Either C is strictly contained in a half-space, or it defines a subspace of X. Since by construction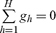 
, C cannot be strictly contained in a half-space. Therefore C defines a subspace. In particular there is H′ ⊂ H, k, and ∀h ∈ H′, λh > 0, such that 
.
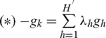Corollary 1: Limited arbitrage is necessary and sufficient for bounded gains from trade in case (ii).
Proof: Consider preferences in case (ii), which include linear preferences. Since Gh = Ah in this case as shown in Proposition 1, the set of traders K defined by k ∈ K ⇔ limj→∞ Uk(gkj) = ∞ equals H. In this case bounded gains from trade imply there can be no sequence {ghj} satisfying (i), (ii), and (iii) in Proposition 2, so the reciprocal of the statement of this proposition is immediate. Thus limited arbitrage is necessary and sufficient for bounded gains from trade when preferences are in case (ii).
This section establishes the existence of an equilibrium in markets with Black Swans. The markets considered in this article allow unbounded short sales, namely the trading domain X is the entire space. This section shows that under the limited arbitrage condition traders only wish to engage in bounded trades with each other, and this implies that the set of efficient trades is compact:
Theorem 1: Limited arbitrage is necessary and sufficient for the compactness of a non-empty Pareto frontier P(E) in markets with Black Swans.
Proof: The result is new and is based on Propositions 1 and 2 above. It extends the results of Chichilnisky (2011) to markets with uncertainty and Black Swans. Assume limited arbitrage is satisfied. Observe that the Pareto frontier is in euclidean space P(E) ⊂ R+H. Proposition 2 showed that with limited arbitrage, P(E) is always bounded. To show compactness it suffices to show that P(E) is closed with limited arbitrage. Without loss of generality, consider a sequence of allocations {ghj}j=1,2,… satisfying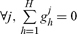 
, so that limj→∞ 
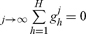, and the corresponding utility values U1 (ghj),…, UH(gHj)∈ R+H. Assume that the utility values converge either to ∞ or to a utility allocation V = (V1,…, VH) ∈ R+H that is undominated by the utility allocation of any other feasible allocation; V may or may not be a utility allocation corresponding to a feasible allocation. When limited arbitrage is satisfied, we show that V is the utility allocation corresponding to a feasible allocation. It suffices to consider the case where the sequence of feasible utility allocations {U1 (g1j),…,UH(gHj)}, and therefore the corresponding allocations {ghj}j=1,2,…, h = 1,…, H are unbounded. Observe that, as shown in the proof of Proposition 2, the countably additive parts of the utilities {U11 (g1j),…, U1H (gHj)}j→∞ are also unbounded in this case; the the normalized sequence {ghj/|| ghj ||}j = 1,2,…, denoted also {ghj}j=1,2,… is weak* precompact by Alaoglu’s theorem, and as shown in the proof of Proposition 2 it has a weak* convergent subsequence, denoted also {ghj}j=1,2,… with a non-zero weak* limit gh = limj→∞{ghj}j=1,2,…. If ∀h, ghj ∉ Gh then eventually the utility values of the traders attain their limit for all h, the utility vector V is achieved by a feasible allocation and the proof is complete. The case when for some trader k, gkj ∉ Gk remains to be considered; without loss assume that ∀h, gkj ∉ Gk remains to be considered. As in Proposition 2, consider the open convex cone C of strictly positive linear combinations of the (non-zero) vectors gh, h = 1, 2, …, H, C = {w = Σhμhgh where ∀h, μh > 0}. Either (a) C is contained strictly in a half-space of X or else (b) C is a subspace of X. By construction ∀j, Σhghj = 0, which eliminates case (a). Therefore case (b) must hold, in particular, there exists k, gk ∈ K and ∀h, λh ≥ 0 satisfying
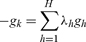
However, limited arbitrage implies that ∃p ∈ ∩hDh so that ∀h, 〈p,gh〉 ≥ 0 , which contradicts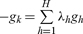 
. The contradiction arises from assuming that the Pareto frontier is not closed under limited arbitrage, therefore P(E) must be closed. Limited arbitrage implies therefore a closed non-empty Pareto frontier P(E) ⊂ RH which, from Proposition 2, is also bounded and hence compact. This establishes sufficiency. The reciprocal is established as follows. Failure of limited arbitrage means, as seen above, that for any (U1(g1),…, U(gH)) ∈ P(E), there exists (v1,…, vH) satisfying ∀h, Σh=1H vh = 0 and Uh(gh + vh) > Uh(gh), a contradiction. Therefore limited arbitrage is necessary for a compact non-empty P(E).
Corollary 2: Limited arbitrage implies that the Pareto frontier P(E) is homeomorphic to a simplex.
This follows from Theorem 1, and the convexity of preferences, Arrow and Hahn (1971), Lemma 3, Chapter 5, p. 81.
Theorem 2: Consider a market with Black Swans E = [X, Uh, Ωh, h = 1,…, H} where H ≥ 2, X = L∞, and ∀h, trader h has a sustainable preference Uh. Then the economy E has a market equilibrium if and only if it satisfies limited arbitrage, and a market equilibrium is Pareto efficient.
Proof: Necessity first. Without loss assume that ∀h, Ωh = 0 ∈ X. Let p* be a price equilibrium and let f* = (f1*,…,fH*) be the corresponding equilibrium allocation. If limited arbitrage fails, ∃h and {gj} ∈ Gh such that 〈p* , gj〉 ≤ 0 for some j >j0 namely gj is affordable at prices p*. Recall that Gh is the same for every allocation by Proposition 1. It follows that ∃j0 > 0 such that for j >j0, Uh(fh* + gj) > Uh(fh*) which, together with the affordability of gj, contradicts the fact that f* is an equilibrium allocation. Limited arbitrage is therefore necessary for existence of an equilibrium.
For sufficiency, Theorem 1 established that the Pareto frontier is homeomorphic to a simplex when limited arbitrage is satisfied. The standard Negishi fixed point argument on the Pareto frontier P(E) in utility space RH establishes therefore the existence of a pseudo-equilibrium, see Negishi (1960) and Chichilnisky and Heal (1984). To complete the proof, observe that ∀h = 1,2,…H, there exists always an allocation in X of strictly lower value than the pseudo-equilibriurn fh* at the price p*. Therefore by Lemma 3, Chapter 4, p. 81 of Arrow and Hahn (1971) the quasi-equilibrium 〈p*,g*〉 is also a competitive equilibrium, completing the proof of existence. Pareto efficiency follows from the fact that the equilibrium is in the Pareto frontier P(E).
The existence of an equilibrium ensures the logical consistency of the concept of markets with Black Swans. The main condition required for existence is limited arbitrage, a condition that has been used to prove existence in the literature (Chichilnisky, 1991, 1994a,b, 1996c,d,e,f, 1998, 2011, 2012a; Chichilnisky and Heal, 1998a), and is extended in this case to markets with Black Swans, where traders have sustainable preferences. The results extend Chichilnisky (2011), which does not include markets with uncertainty.
The notion of an equilibrium price in a market with Black Swans requires further discussion. An equilibrium price is defined here — as is usual — as a continuous linear function on commodities or trades, and this price establishes the economic value of commodities at a market equilibrium. The space of prices is here L∞*, the dual of the space of commodities L∞ that has been characterized (see the Appendix) as consisting of the linear sum of two subspaces, one subspace consisting of prices in L1 that have a ready interpretation, and the second subspace consisting of finitely additive measures on R that require further explanation. Since preferences are sustainable, a price equilibrium will have the same form as a sustainable preference as characterized above and in Chichilnisky (1996a,b), namely a convex combination of a path of prices through time that is an element of L1 and of a purely finitely additive measure; for example, a measure that focuses its weight on rare events. In this context, therefore, a market price may assign two types of economic values: (i) a value to commodities in the various (frequent) states of nature, and in addition (ii) a value to commodities in rare and catastrophic states. The second term (ii) may seem unusual in standard markets, but it seems entirely appropriate for a market equilibrium in economies with Black Swans. It modifies the conventional notion of prices just as is needed to value rare events that are potentially catastrophic, as seems required for markets with Black Swans.
A finitely additive part of the price that assigns value to rare events establishes a connection between sustainable markets and the “Uncertainty Principle” through the “Axiom of Choice” in the foundation of mathematics, which postulates that there exists a universal and consistent fashion to select an element from every set; see Dunford and Schwartz (1958), Yosida (1974), Yosida and Hewitt (1952), Chichilnisky and Heal (1997), Kadane and O’Hagan (1995), Purves and Sudderth (1976), Dubins (1975), and Dubins and Savage (1965). This principle establishes the existence of propositions that cannot be proven to be true or false, the “incompleteness of mathematics.” The Axiom of Choice has been proven by Godel (1940) to be independent from the rest of mathematics, so that statements that require this axiom are neither true nor false by themselves, but their validity depends on the axiomatic foundation that one chooses.
It is possible to illustrate — but not in general construct — a purely finitely additive measure on R, or on any finite open interval (a, b) of R, see examples in Chichilnisky (2010a,b). This issue of constructibility is not unique to markets with Black Swans: it is an issue shared by the proof of the second fundamental theorem of welfare economics, see Debreu (1953), which requires the Hahn-Banach theorem and therefore the Axiom of Choice. The proof of existence of such purely finitely additive functions can be achieved in various ways, but each requires the Axiom of Choice or a related result. To illustrate the problem, consider the function (g(t)) = limt→∞ g(t) that is defined only on a closed strict subspace L′∞ of L∞ consisting of functions that have a limit at infinity. This function is continuous and linear on L′∞. One can use Hahn–Banach’s theorem to extend this function the closed subspace L′∞ ⊂ L∞ to the entire space L∞ preserving the norm. Since the extension is not in L1 it defines a purely finitely additive measure, as shown in the Appendix. However, in a general form Hahn–Banach’s theorem requires the Axiom of Choice, which has been shown to be independent from the rest of the axioms of mathematics (Godel, 1940). Alternatively, one can extend the notion of a limit to encompass all functions in L∞ including those with no standard limit. This can be achieved by defining convergence along a free ultrafilter arising from Stone–Cech compactification of the real line R as in Chichilnisky and Heal (1997). However, the existence of a free ultrafilter requires once again the Axiom of Choice (Godel, 1940). This illustrates why the actual construction of a purely finitely additive measure requires the Axiom of Choice. Since sustainable markets have prices that include purely finitely additive measures, this provides a connection between the Axiom of Choice and sustainable markets. It appears that the consideration of rare events that could be catastrophic conjures up the Axiom of Choice that is independent from the rest of mathematics (Godel, 1940).
Example: A preference that is sensitive to Black Swans but insensitive to frequent risks
Consider W(f) = lim infx∈R(f(x)). This utility is insensitive to the frequent risks and therefore does not satisfy Axiom 2. In addition this map is not linear, failing Axiom 3.
The dual space L∞*: countably additive and purely finitely additive measures
See Yosida (1974), Yosida and Hewitt (1952), Dunford and Schwartz (1958). A measure η is called finitely additive when for any family of pairwise disjoint measurable sets 
. The measure η is called countably additive when for any countable family of pairwise disjoint measurable sets 
. The space of continuous linear functions on L∞ is the “dual” of L∞, and is denoted L∞*. This space has been characterized, e.g. in Yosida (1974) and Yosida and Hewitt (1952). L∞* = L1 + (L∞1 − L1): it consists of L1 functions g that define countably additive measures v on R by the rule 
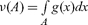where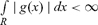 
so that v is absolutely continuous with respect to the Lebesgue measure, plus measures that are not countably additive, also called purely finitely additive measures, forming a subspace denoted L∞1 − L1. While a countable measure can be identified with an L1 function, namely its so called “density,” purely finitely additive measures cannot be identified by such functions.
This research was conducted at the Columbia Consortium for Risk Management (CCRM) directed by the author at Columbia University in New York, and its Program on Information and Resources (PIR). We acknowledge support from Grant No 5222–72 of the US Air Force Office of Research (AFOSR). The initial results on sustainable preferences were presented as an invited address at Stanford University’s 1993 Seminar on Reconsideration of Values, organized by Kenneth Arrow, in 2000 at the Fields Institute for Mathematical Sciences in Toronto Canada, at the 2005 NBER Conference Mathematical Economics: The Legacy of Gerard Debreu at UC Berkeley, at the Department of Economics of the University of Kansas National Bureau of Economic Research General Equilibrium Conference, September 2006, the Department of Statistics of the University of Oslo, Norway, Fall 2007, the Department of Statistics of Columbia University, Fall 2007, the AFOSR in Arlington VA, January 2009, Dayton Ohio 201, and Arlington VA January 2011, and the Colloqium at the Mathematics Department and the Institute for Behavioral Sciences of the University of California at Irvine, May 18, 2011. We thank the above institutions and individuals for supporting the research as well as Eduardo Jose Chichilnisky, Salk Institute, La Jolla, California, Lance Taylor and two anonymous reviewers, for valuable comments and suggestions.
1 Within economies with infinitely many states of nature, for example, the “cone condition” introduced by Chichilnisky and Kalman (1980), also known as “properness,” and frequently to prove existence of market equilibrium with infinitely many states of nature (cf. Yannelis and Zame, 1986; Chichilnisky, 1993), a form of averaging of risks is required that once again underestimates Black Swan events, Chichilnisky (2000, 2002). Chichilnisky (1993) showed that the original “cone condition” is the same as the later condition named “properness.” This condition as shown below in this chapter implies optimizing utility functions which — as in the case of expected utility — are insensitive to rare but catastrophic events.
2 The G-20 Meeting took place in Pittsburgh, USA, 24–25 September 2009. The G-20 Leaders’ Statement can be found at http://www.pittsburghsummit.gov/mediacenter/129639.htm. Here are relevant quotes from the Leaders’ Statement: “As we commit to implement a new, sustainable growth model,weshould encourage workonmeasurement methods so as to better take into account the social and environmental dimensions of economic development.” and “Modernizing the international financial institutions and global development architecture is essential to our efforts to promote global financial stability, foster sustainable development, and lift the lives of the poorest.” These statements substantiate the extent to which sustainable development has become a mainstream international priority.
3 The link between sustainability, poverty, and development is deep and critical. The subject exceeds the scope of this chapter and the reader is referred for example to Chichilnisky and Sheeran (2009) and Chichilnisky (1994).
4 With infinitely many states of nature, compactness requires weaker topologies that can imply insensitivity towards rare events (Yannelis and Zame, 1986). Furthermore, supporting prices that are continuous with the “sup norm” can lead to paradoxical results (Chichilnisky and Kalman, 1980). To resolve this continuity–compactness dilemma and avoid paradoxes we rely on the properties of sustainable preferences that are sensitive to the present and the future, and use the notion of “limited arbitrage” introduced in Chichilnisky (1991, 1994a, 1996c, 1998). Taken together, sustainable preferences and the notion of limited arbitrage, overcome the problems of insensitivity to rare events and unlimited short sales by limiting somewhat the diversity of the traders (Chichilnisky, 1994b), bounding the “gains from trade” that they can achieve trading with each other, while creating sensitivity to frequent and rare events and ensuring existence of solutions. In Proposition 2, we show that limited arbitrage is equivalent to bounded gains from trade, and it ensures the compactness of Pareto utility allocations, as needed for the existence of solutions, based on earlier results of Chichilnisky (1991, 1998) and Chichilnisky and Heal (1984, 1998). To complete the existence result, Theorem 1 proves that, in a sustainable market, limited arbitrage is equivalent to the compactness of the set of Pareto efficient allocations, and Theorem 2 establishes that it is necessary and sufficient for the existence of sustainable as well as efficient competitive market equilibrium. The next section discusses the role of prices in a sustainable market economy. These assign economic value both to instantaneous and long-run consumption, providinga connection with the axiom of choice that is at the foundation of mathematics. It ought to be clarified that a sustainable market equilibrium is shown to exist, but it is a somewhat different concept than what is normally defined as a market equilibrium, since in sustainable markets, market prices take a new role: they represent the value of consumption with frequent risks as well as the value of consumption in Black Swans risks — a concept that differs from currently used market equilibrium prices. Indeed, when sustainable constraints are taken into consideration, new concepts and features of economics arise as demonstrated throughout this entire special volume on the economics of the global environment, see Asheim, Mitra, and Tungodden (2011), Burniaux and Martins (2011), Chipman and Tian (2011), Dutta and Radner (2011), Figuieres and Tidball (2011), Karp and Zhang (2011), Lauwers (2011), Lecocq and Hourcade (2011), and Rezai, Foley, and Taylor (2011).
5 The axioms for sustainable preferences were introduced in Chichilnisky (1996a,b), and similar axioms were introduced for the foundations of preferences under uncertainty, for non-parametric econometrics (Chichilnisky, 2009a,b), for relative likelihoods and the foundations of probability and statistics (Chichilnisky, 2010a,b).
6 The time preference U ranks paths over time u(t)∈ L∞ and Axiom 1 requires U to be continuous and linear. Observe that since the instantaneous utility function u : RN → R is concave and need not be linear, the ranking of consumption paths need not be linear as a function of consumption, x(t).
7 The cones C(Ω) = {{f} ⊂ X : limj→∞f j = U(jj0) for some j0} are also convex and uniform across vectors Ω.
8 This follows from the initial results of Chichilnisky (1996a,b). L∞* − L1 denotes the complement of L1 in L∞*, namely the space of purely finitely additive measures, see also the Appendix.
Arrow, K. (1971) Essays in the Theory of Risk Bearing, Markham Publishing Co., Chicago.
Arrow, K. J., and Hahn, F. (1971) General Competitive Analysis. Holden-Day, San Francisco.
Asheim, G., Mitra, T., and Tungodden, B. (2011) Sustainable Resources: Social Welfare Functions, Economic Theory Special Issue on the Global Environment.
Burniaux, J.-M., and Martins, J.O. (2011) Carbon Leakages: A General Equilibrium View, Economic Theory Special Issue on the Global Environment.
Chichilnisky, G. (1991) Limited Arbitrage is Necessary and Sufficient for the Existence of Competitive Equilibrium With or Without Short Sales, Discussion Paper No. 650, Columbia University Department of Economics, December 1991. Also in Economic Theory 95, 79–;108, 1995.
Chichilnisky, G. (1993) The Cone Condition, Properness and Extremely Desirable Commodities, Economic Theory 3, 177–;182.
Chichilnisky, G. (1994a) Arbitrage and Gains from Trade: A United Perspective on Resource Allocation, American Economic Review 84, 427–;434.
Chichilnisky, G. (1994b) Limited Arbitrage is Necessary and Sufficient for the Existence of a Competitive Equilibrium and the Core, and it Limits Voting Cycles Economics letters 46, 321–;331.
Chichilnisky, G. (1996a) An Axiomatic Approach to Sustainable Development, Social Choice and Welfare 13, 231–;257.
Chichilnisky, G. (1996b) What is Sustainable Development?, Resource Energy Economics 73, 467–;491.
Chichilnisky, G. (1996c) Markets with Endogenous Uncertainty: Theory and Policy, Theory and Decision 41, pp. 99–;131.
Chichilnisky, G. (1996d) Updating Von Neumann Morgenstern Axioms for Choice under Catastrophic Risks, Invited Presentation, Proceedings of a Workshop on Catastrophic Environmental Risks, The Fields Institute for Mathematical Sciences, University of Toronto, Canada, June 9–;11.
Chichilnisky, G. (1996e) Markets and Games: A Simple Equivalence Among the Core, Equilibrium and Limited Arbitrage Metroeconomica 47, 266–280.
Chichilnisky, G. (1996f) Limited Arbitrage is Necessary and Sufficient for the Non-emptiness of the Core Economics letters 52, 177–180.
Chichilnisky, G. (1996g) Financial Innovation in Property Catastrophe Reinsurance: The Convergence of Insurance and Capital Markets Risk Financing Newsletter 13(2), June.
Chichilnisky, G (1997a) What Is Sustainable Development, Land Economics 73, 467–491.
Chichilnisky, G. (1997b) Property Cat Woes Have Financial Solutions, World Reinsurance Report September 1, s-20–;s-24.
Chichilnisky, G. (1998) A Unified Perspective on Resource Allocation: Limited Arbitrage is Necessary and Sufficient for the Existence of a Competitive Equilibrium, the Core and Social Choice, in G. Chichilnisky (Ed.), Topology and Markets, Fields Institute for Research in Mathematical Sciences and the American Mathematical Society, Toronto, Canada.
Chichilnisky, G. (1999) Catastrophe Futures: Financial Markets for Unknown Risks, in G. Chichilnisky (Ed.) Markets, Information, and Uncertainty, Cambridge University Press, pp. 120–140 (with G. Heal).
Chichilnisky, G. (2000) An Axiomatic Approach to Choice Under Uncertainty with Catastrophic Risks, Resource & Energy Economics 22, 221–231.
Chichilnisky, G. (2002) Catastrophic Risk, in AH. EIShaarawi and WW. Piegorsch (Eds.) Encyclopedia of Environmetrics Volume 1, John Wiley & Sons, Ltd, Chichester, pp. 274–279.
Chichilnisky, G. (2006) Catastrophic Risks: The Need for New Tools, Financial Instruments and Institutions, in Privatization of Risk, Social Science Research Council, June.
Chichilnisky, G. (2009a) The Limits of Econometrics: Non Parametric Estimation in Hilbert Spaces, Econometric Theory 25, 1070–1086.
Chichilnisky, G. (2009b) The Topology of Fear, Journal of Mathematical Economics 45, 807–816.
Chichilnisky, G. (2009c) Catastrophic Risks, International Journal of Green Economics 3, 130–141.
Chichilnisky, G. (2009d) Avoiding Extinction: Equal Treatment of the Present and the Future, Economics: The Open-Access, Open-Assessment E-Journal 3, 200932, 1–25.
Chichilnisky, G. (2010a) The Foundations of Statistics with Black Swans, Mathematical Social Sciences 59, 184–192.
Chichilnisky, G. (2010b) The Foundations of Probability with Black Swans, Journal of Probability and Statistics, Article ID 838240.
Chichilnisky, G. (2011) Catastrophic Risks with Finite of Infinite States, International Journal of Ecological Economics & Statistics 23, 3–18.
Chichilnisky, G. (2012a) Sustainable Markets with Short Sales, Journal of Economic Theory 49(2), 293–308.
Chichilnisky, G. (2012b) Economic Theory and the Global Environment, Journal of Economic Theory 49(2) 217–226.
Chichilnisky, G., and Chanel, O. (2009a) The Influence of Fear in Decisions: Experimental Evidence, Journal of Risk and Uncertainty 39(3), 271–298.
Chichilnisky, G., and Chanel, O. (2012) Valuing Life: Experimental Evidence Using Sensitivity to Rare Events, Ecological Economics, March S.
Chichilnisky, G., and Heal, G.M. (1984) Existence of a Competitive Equiibrium in Sobolev Spaces without Bounds on Short Sales, Journal of Economic Theory 59, 364–384. Initially circulated as Chichilnisky, G., and Heal, G.M, Existence of a Competitive Equilibrium in Lp and Sobolev Spaces, IMA Preprint series #79, Institute for Mathematics and its Applications, University of Minnessota, Minneapolis, Minnesota, June 1984.
Chichilnisky, G., and Heal, G.M. (1997) Social choice with infinite populations, Social Choice and Welfare 14, 303–319.
Chichilnisky, G., and Heal, G.M. (1998a) A Unified Treatment of Finite and Infinite Economies: Limited Arbitrage is Necessary and Sufficient for the Existence of Equilibrium and the Core, Economic Theory 12, 163–176.
Chichilnisky, G., and Heal, G.H. (1998b) Global Environmental Risks, in G. Chichilnisky, G.M. Heal, and A. Vercelli (Eds.), Sustainability: Dynamics and Uncertainty, Kluwer Academic Publishers, The Netherlands 23–46.
Chichilnisky, G., and Heal G.M. (1998c) Managing Unknown Risks: The Future of Global Reinsurance, The Journal of Portfolio Management 24, 85–91.
Chichilnisky, G., and Kalman, P. (1980) An Application of Functional Analysis to Models of Efficient Allocation of Economic Resources, Journal of Optimization Theory and Applications 30, 19–32.
Chichilnisky, G., and Sheeran, K. (2009) Saving Kyoto. New Holland Publishers, London.
Chichilnisky, G., and Wu, H.-M. (2006) General Equilibrium with Endogenous Uncertainty and Default, Journal of Mathematical Economics, 42.
Chipman, J., and Tian, G. (2011) Detrimental Externalities Pollution Rights and the “Coase Theorem”, Economic Theory Special Issue on the Global Environment.
Debreu, G. (1953) Valuation Equilibrium and Pareto Optimum, Proceedings of the National Academy of Sciences 40, 588–592.
DeGroot, M. (2004) Optimal Statistical Decisions. Wiley-Interscience, New York.
Dubins, L. (1975) Finitely Additive Conditional Probabilities, Conglomerability and Disintegration, The Annals of Probability 3, 89–99.
Dubins, L., and Savage, L. (1965) Inequalities for Stochastic Processes: How to Gamble if You Must, McGraw Hill, New York.
Dunford, N., and Schwartz, J.T. (1958) Linear Operators, Part I, Interscience, New York.
Dutta, P., and Radner, R. (2011) Capital Growth in a Global Warming Model, Economic Theory Special Issue on the Global Environment.
Figuieres, C., and Tidball, M.(2011) Sustainable Exploitation of a Natural Resource: a Satisfying Use of Chichilnisky’s Criterion, Economic Theory Special Issue on the Global Environment.
Godel, K. (1940) The Consistency of the Continuum Hypothesis. Annals of Mathematical Studies 3, Princeton University Press, Princeton.
Hernstein, I.N., and Milnor, J. (1953) An Axiomatic Approach to Measurable Utility, Econometrica 1, 291–297.
Kadane, J.B., and O’Hagan, A. (1995) Using Finitely Additive Probability: Uniform Distributions of the Natural Numbers, Journal of the American Statistical Association 90, 525–631.
Karp, L., and Zhang, J. (2011) Taxes v. Quantities for a Stock Pollutant with Endogenous Abatement Costs and Asymetric Information, Economic Theory Special Issue on the Global Environment.
Koopmans, T.C. (1960) Stationary Ordinal Utility and Impatience, Econometrica 28, 287–309.
Koopmans, T.C. (1972) Representation of Preferences Orderings Over Time, in B. McGuire and R. Radner (Eds.), Decision and Organization, North Holland Amsterdam.
Lauwers, L. (1993) Infinite Chichilnisky Rules, Economics Letters 4, 349–352.
Lauwers, L. (2011) Intergenerational Equity, Efficiency and Constructability, Economic Theory Special Issue on the Global Environment.
Lecocq, F., and Hourcade, J.C. (2011) Unspoken Ethical Issues in the Climate Affair: Insights from a Theoretical Analysis of the Negotiations, Economic Theory Special Issue on the Global Environment.
Negishi, T. (1960) Welfare Economics and Existence of an Equilibrium for a Competitive Economy, Metroeconomica 12, 92–97.
Ostrom, E. (2011) Nested Externalities and Polycentric Institutions: Must We Wait for Global Solutions to Climate Change before Taking Actions at Other Scales?, Economic Theory Special Issue on the Global Environment.
Posner, R. (2004) Catastrophes: Risk and Response, Oxford University Press, Oxford.
Purves, R.W., and Sudderth, W.D. (1976) Some Finitely Additive Probability, The Annals of Probability 4, 259–276.
Rezai, A., Foley, D., and Taylor, L. (2011) Global Warming and Economic Externalities, Economic Theory Special Issue on the Global Environment. The World Bank, State and Trends of the Carbon Market, Carbon Finance at the World Bank, Annual Publication 2005–2012.
Yannelis, N., and Zame, W. (1986) Equilibria in Banach Lattices without Ordered Preferences, Journal of Mathematical Economics 15, 85–110.
Yosida, K. (1974) Functional Analysis, 4th edition, Springer Verlag, New York and Heidelberg.
Yosida, K., and Hewitt, E. (1952) Finitely Level Independent Measures, Transactions of the American Mathematical Society 72, 46–66.