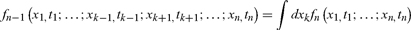
| 8 | Equilibrium vs. market efficiency |
| Joseph L. McCauley |
Rational expectations (Sargent, 1987) confuses stationary markets with efficient markets. We will explain why efficient markets and equilibrium markets are mutually contradictory, why if you have “efficiency” then you cannot have equilibrium (McCauley, 2009). An efficient market admits no equilibrium, so it exhibits no stationary price. In stark contrast, a stationary market would necessarily fluctuate about an equilibrium price, a stationary price. Rational expectations includes contradictory ideas because equilibrium is contradictorily defined in economics (McCauley, 2009). Strange as it seems, assumptions of equilibrium in economics are marked by lack of attention to the precise definition of equilibrium in dynamical systems theory, physics, and the theory of stochastic processes. There’s an historic reason for this.
From an historical standpoint, rational expectations can be seen as the successful attempt to introduce randomness without contradicting the neo-classical economic model (McCann, 1994). Muth (1961: 315) introduced randomness into prices by assuming a fluctuating ad hoc excess demand. He then set the excess demand equal to zero and derived a fluctuating price, which he mis-identified as equilibrium. Prices are stationary in equilibrium, and vanishing excess demand can only imply a stationary price. Muth’s ad hoc definition of excess demand was incorrect, it was not derived from empirical analysis.
In equilibrium, correctly defined, all one-point averages are constant, and all pair correlations depend only on the lag time T, not the time t at which observations begin (McCauley, 2009). Real markets are nonstationary, with very different behavior of one-point averages and pair correlations, as we’ll show below. Muth and his successors did not look carefully enough at their assumptions: we’ll also show that it’s quite easy to devise a very simple trading strategy to suck money systematically out of a hypothetical equilibrium market. That cannot be done in an efficient market.
A Markov process has no memory. The conditional probability density depends only on the present state and the last observed state. In particular, the drift and diffusion coefficients may depend only on the present state and on no state from the past.
An example of a martingale is a drift-free Markov process. More generally, the conditional expectation of the random variable x(t) in a martingale is the last observed state x(t − T), 〈x(t)〉 = x(t − T). This means that the pair correlations obey
〈x(t)x(t−T)〉 = 〈x2 (t − T)〉 = σ2 (t − T)
where σ2(t) is the variance at time t. We will refer to Markov processes and martingales in what follows.
Following Kolmogorov, a stochastic process can be defined in principle by specifying the corresponding infinite hierarchy of n-point densities. To identify a class of process we need at least the two-point density, or the pair correlations. In practice, one generally cannot measure densities (unless scaling holds) but one can sometimes measure pair correlations. We will depend on the latter.
Let (x1,…,xn) represent observed points in a time series at times (t1,…,tn) where tk < tk+1. Finance markets generate time series that reflect a certain class of stochastic process, as we will explain below. As we have stated above, a stochastic process x(t) would be precisely specified/defined by the infinite hierarchy of n-point densities (Gnedenko, 1967; Stratonovich, 1963)
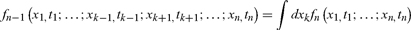 |
(1) |
so that, e.g.,
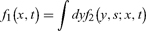 |
(2) |
and
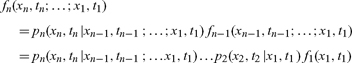 |
(3) |
where pn is the transition density depending on n points. In finance, x(t) = ln S(t)/Sc(t) is the log return where S(t) is the price of the underlying asset (stock, bond, or foreign exchange) at time t. The price Sc(t) locates the peak of the one-point returns density f1(x, t) at time t and so is consensus value, or just “value.” “Value” is simply the price that the largest fraction of agents agree on at any given point of time, the most probable price. There is no assumption of market clearing or equilibrium, this definition of value is not restricted to equilibrium. In particular, it applies to both nonstationary and hypothetical stationary markets (McCauley, 2009).
Could value be known, then we could distinguish undervalued from overvalued. Radio engineers knew in the 1930s that one-point densities cannot be measured, there’s too much scatter in the data. However, certain averages can be reliably measured (Bassler, McCauley, and Gunaratne, 2007: 17297; Bassler, Gunaratne, and McCauley, 2008: 769; McCauley, 2008a: 5188). We know in principle what we mean by the notion of “value” but we cannot expect to be able to measure it. What do we need in order to pin down an underlying class of stochastic dynamics generating the market? Value is therefore of no practical use in trading, whatever traders may believe.
The one-point density defines value, but a one-point density cannot pin down an underlying stochastic process; completely different classes of process can exhibit the same one-point density (Hänggi and Thomas, 1977; McCauley, 2010). Pair correlations provide the lowest level of description of a class of stochastic processes, so we need at least the two-point density f2 or the two-point conditional density p2 in order to have any hope of understanding the underlying dynamics. In practice, the two-point density cannot be extracted from data due to scatter, so we need to measure the pair correlations 〈x(t + T)x(t)〉 from time series analysis.
Muth (1961) introduced and Lucas (1972) propagated the contradictory formulation of rational expectations. Ignoring those historic misleading notions, we can formulate the idea of a hypothetical equilibrium market correctly.
A stationary random process reflects the generalization of equilibrium to a stochastic process. Here, prices fluctuate about an equilibrium price that we can identify as “value.” Value in such a market is time-invariant because the one-point density is time-independent. That is, “value” would be fixed once and for all in a stationary market. We could distinguish over- from under-valued if we could find an equilibrium market and then measure the one-point density.
Adhering to precise definitions in mathematics and physics, the correct definition of equilibrium in a stochastic process is: all averages are time-invariant. So in a stationary process, all densities fn and all transition densities pn of all orders n must be time translationally invariant (McCauley, 2009; Gnedenko, 1967; Stratonovich, 1963):
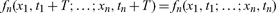 |
(4) |
p2(xn, tn |xn−1, tn−1) =p2(xn,T |xn−1, 0)
as well.
It follows that the normalizable one-point density f1 (x) is t-independent, so that the mean 〈x(t)〉, variance σ2 = 〈x2(t)〉 − 〈x(t)〉2 , and all one-point averages are constants.
The one-point density describes fluctuations about statistical equilibrium. A warning: stationary processes may be Markovian, but time translationally invariant Markov processes are generally not stationary. In a time translationally invariant Markov process a normalizable t-independent one-point density generally doesn’t exist (McCauley, 2009). The Wiener process (known in economics as “white noise”) is the simplest example of a nonequilibrium Markov process.
Under stationarity, time translational invariance of the transition density p2(xn, t + T |xn−1, 0) implies pair correlations
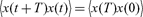 |
(5) |
depending on lag time T alone, independent of starting time t. With no drift this yields if x(0) = 0. In practice, constant mean and variance and a pair correlation depending on time lag alone are the empirical signatures of statistical equilibrium. However, an equilibrium market could not clear pointwise due to fluctuations: only a small fraction of agents (those with prices near the peak of the one-point density) agree on price. In the neo-classical straightjacket every agent agrees on price in equilibrium. Sociologically seen, trying to enforce this notion is the reason for Muth’s historic mistake.
The title of this section refers to the explanation by Merton and Scholes to a trader of what they were trying to do with the Black–Scholes option pricing model, suck nickels out of finance markets as with a vacuum cleaner (The Trillion Dollar Bet, no date). They, too, believed in a contradictory notion of market equilibrium, and failed catastrophically (Dunbar, 2000) because markets do not “return to historic values” in the long run. Recurrence would hold in an equilibrium market, but not in a nonstationary one.
Recurrence is the generalization to nonperiodic systems of the notion of simple periodicity. A system is periodic if an initial state repeats precisely after a definite amount of time τ, which is called the period. Generally, there is no period but there may be recurrence. A state is said to recur if after a finite amount of time the trajectory passes within a specified finite distance of the initial state. The amount of time required increases as you reduce the distance from the initial state and the nearby state, and there is no period. Stationary processes are generally recurrent.
It’s trivial to devise a trading strategy that allows you to beat an equilibrium market (McCauley, 2009). Under stationarity, one knows that the prices will repeatedly fluctuate about equilibrium. When the price drops a standard deviation from value, for example, then buy. Hold until the price hits value plus one standard deviation and then sell. Such fluctuations are systematically guaranteed, you can even calculate the recurrence time (McCauley, 2010) by using Ito’s lemma along with the construction of a suitable martingale. With recurrence guaranteed, a trader could suck money out of an equilibrium market systematically with little or no risk. The trader need only have enough cash to survive without having to sell before the expected price increase appears (bet/cash should always be small). Because you’re only trading on equilibrium fluctuations, the buy/sell strategy can be repeated ad infinitum. It’s clear that an equilibrium market can’t be efficient, if by efficient we mean a market that’s hard or impossible to beat (Mandelbrot, 1966).
Finance markets are nonstationary. Equilibrium is not found either in the historically best-known model (Gaussian returns; Osborne, 1964; Black and Scholes, 1973) or in real data (Bassler et al., 2007, 2008; McCauley, 2008b). What class of model characterizes a finance market?
Here and in all that follows we assume a normal liquid market, a market where the “noise traders” (Black, 1986) trade frequently enough that bid/ask spreads are very small relative to price (McCauley, 2009). A crash is not a normal liquid market. In a crash liquidity dries up. To zeroth order, there are many limit orders to sell with few or no buyers in a market crash. A market crash is certainly not a fluctuation described by fat tails in a one-point returns distribution, a market crash is instead a liquidity drought. That’s what happened to LTCM in 1998, and housing-based financial instruments in September 2007 and in 2008 (McCauley, 2009).
Due to the sparseness of data it’s impossible to model a crash falsifiably. But there are nonmathematical signs that a bubble is about to burst. These signs take the form of unusually risky behavior, as described in McKay (1980) and Kindelberger (1996). Before the stock market crash of 2000 ordinary people quit their jobs, mortgaged their houses a second time and used the cash in “day trading.” Leading up to the derivatives crash of 2007–8, some agents bought houses for the short term to resell for a profit, houses were bought and resold as if they were hot stocks. The market crash of 1929 led to a liquidity crisis. The reason that crashes between 1960 and 2000 did not lead to a liquidity crisis, but the 2007–8 crash did, is described elsewhere (McCauley, 2009).
By the efficient market hypothesis (EMH), we mean a detrended normal liquid market that is in principle impossible to beat systematically. This means that there are no readily available correlations or patterns that can be exploited for profit. A Markovian market would be unbeatable in this sense, because a detrended Markov market has no memory to exploit. A detrended Markov process is very generally nonstationary without time translational invariance, and recurrence of prices cannot be predicted or expected. More generally, a detrended Markov process is a martingale, but the reverse is not necessarily true. Martingales behave Markovian at the level of pair correlations even if the entire process has nonMarkov features, like memory of an initial condition in the distant past (Hänggi and Thomas, 1977; McCauley, 2010). However, that sort of trivial memory cannot be exploited for financial advantage.
To formulate the dynamics of hard-to-beat markets, we assume that the increment autocorrelations vanish, where by increments we mean differences in levels x(t, T) = x(t + T) − x(t), x(t, −T) = x(t) − x(t− T). The statement that trading during an earlier time interval provides no signals for traders in a later nonoverlapping time interval at the level of pair correlations is simply that
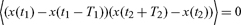 |
(6) |
if there is no time interval overlap, [t1 − T1, t1]∩[t2, t2 + T2] = Ø, where Ø denotes the empty set on the line. This is a very different condition than assuming that the increments are statistically independent, and is much weaker than assuming that the market is Markovian.
Consider any stochastic process x(t) where the differences are uncorrelated, meaning that (6) holds. From this condition we obtain the autocorrelation function for levels (returns). Let t > s, then
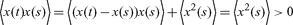 |
(7) |
since x(s) − x(t0) = x(s), so that 〈x(t + T)x(t)〉 is simply the variance in levels x(t) at the earlier time t. This condition is equivalent to a martingale process:
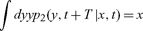 |
(8) |
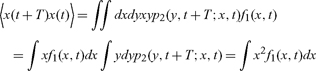 |
(9) |
At the level of pair correlations, a martingale cannot be distinguished from a drift-free Markov process. Note also that (6) can be interpreted as asserting that earlier returns have no correlation with future gains. This condition can’t be assumed, it must be deduced via data analysis.
Next, we emphasize the key point for data analysis and modeling. Combining
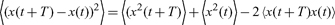 |
(10) |
with (10) we get
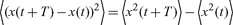 |
(11) |
which depends on both t and T, excepting the rare case where 〈x2〉 is linear in t. Uncorrelated differences are generally nonstationary (this is bad news for cointegration1).
It’s easy to show that, with one rare exception, time-translationally invariant martingales are nonstationary processes. The daily and weekly behavior of this mean square fluctuation has been described in (Bassler et al., 2007: 17297; Bassler et al., 2008: 769) for foreign exchange (FX) markets.
The difference correlations of a stationary process do not vanish,
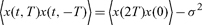 |
(12) |
reflecting pair correlations that can be traded on for profit. Price recurrence is the basis for a successful trading strategy in a hypothetical stationary market. Real markets are martingales, nonstationary processes with nonstationary differences.
A successful mathematics-based trading strategy should carry with it the prediction of the first passage time, which is related to the idea of recurrence. For a martingale without time translational invariance the standard procedure for calculating the first passage time fails. The question of how to formulate the first passage time for a general nonstationary process is hard to answer.
A first passage time is a relaxation of the condition of recurrence, albeit it is related in spirit. Given the present price of a stock, what is the average waiting time for the stock to hit an entirely different price? Clearly, formulating this problem requires as a first step that we know the dynamical model that generates the stock prices. All that we know is that we have the martingale class, with the first difference x(t, T) = x(t + T)− x(t) given as (Bassler et al., 2007)
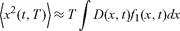 |
(13) |
for T « t but we cannot say which martingale. Martingales are diffusive processes but the diffusion coefficient D(x, t) is constant or t-dependent only for the Wiener process or for transformations on Wiener processes. A constant diffusion coefficient would imply Gaussian returns, but the observed returns are not Gaussian. The observed returns can be fit by an exponential density during a certain time interval of day (McCauley, 2009). Qualitatively, a variable diffusion coefficient (one dependent on both returns and time) describes systematic nonuniformities in traders’ behavior. This is discussed in Seemann, McCauley, and Gunaratne (2011) for the exponential density, e.g.
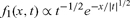 |
(14) |
the diffusion coefficient is
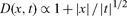 |
(15) |
The t-dependence of (13) has been measured for FX markets (McCauley, 2009; Bassler et al., 2007, 2008; Seeman et al., 2011) but far more data would be required (a 30 years long time series would not be enough) to extract the diffusion coefficient D(x,t).
The exponential model (14,15) with a different Hurst exponent H (H = 1/2 in (14,15)) can be used to fit FX returns over a certain time interval during daily trading. FX returns over longer time intervals do not scale. Scaling with 0 < H < 1 is described, with u = |x|/|t|H, by
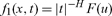 |
(16) |
and
D(x,t) = |t|2H−1D(u)
The financial martingale describes a nonstationary process where the variance grows linearly with the time, so is not approximable by stationarity. But back to the question of recurrence.
By construction, this martingale is nonstationary with nonstationary differences. If we could formulate and solve the problem of first passage time for a martingale without time translational invariance then we could address the question of a profitable trading strategy quantitatively. We might also be able to analyze the following problem: if two stocks appear to be significantly relatively mispriced, then how long should we expect to wait to see the discrepancy disappear? Here’s the fundamental difficulty with trying to formulate and solve all such questions.
The standard method for formulating a first passage time assumes a time-translationally invariant stochastic process, a process where D(x,t) = D(x). In that case the first passage time problem can be reduced to the solution of an ordinary differential equation. If the diffusion coefficient depends inseparably on both x and t, then that method cannot be used. In a word, we do not even understand how to formulate the problem. There is therefore no reliable mathematical prediction to tell us that we should bet on a return to parity of two stocks that are (subjectively) judged to be relatively mispriced. This degree of ignorance does not prevent trading houses from promoting short and long trades based on the idea of mispricing. LTCM’s experience of the Gamblers’ Ruin in October 1997 was based on a misplaced belief in recurrence, that was shown to be wrong when liquidity dried up for Russian bonds (Dunbar, 2007). This chapter does not provide much that’s of interest for banks and traders, except advice on how not to go broke, and on how to avoid causing financial crises.
This contribution is dedicated to the festschrift for my good friend Duncan Foley. Duncan has long been interested in equilibrium vs. nonequilibrium in economics, and in fundamental ideas in economics. I hope that he will enjoy my small contribution to the celebration of his life and teaching. This chapter reflects work done with Gemunu Gunaratne, Kevin Bassler, and Lars Seemann. I’m grateful to Duncan for a very nice endorsement of my 2009 book (McCauley, 2009), and for many interesting and very helpful email exchanges on various aspects of economics and finance. The background required to understand this chapter in depth is developed in my book, which was written for both students and experts.
1 Cointegration is a method for describing how two entirely different time series, like FX rates, and relative price levels in two countries, should behave. The method assumes stationary increments except in special cases, but differences between different financial time series are not stationary (McCauley, 2009).
Bassler, K.E., McCauley, J.L., and Gunaratne, G.H. (2007) Nonstationary Increments, Scaling Distributions, and Variable Diffusion Processes in Financial Markets, PNAS 104, 17297.
Bassler, K.E., Gunaratne, G.H., and McCauley, J.L. (2008) Empirically Based Modeling in Finance and Beyond and Spurious Stylized Facts, Int. Rev. Fin. An. 17, 769.
Black, F. (1986) Noise, J. of Finance 3, 529.
Black, F., and Scholes, M. (1973) The Pricing of Options and Corporate Liabilities, J. Political Economy 81, 637.
Dunbar, N. (2000) Inventing Money, Long-Term Capital Management and the Search for Risk-Free Profits, New York: Wiley.
Gnedenko, B.V. (1967) The Theory of Probability, tr. by B.D. Seckler, New York: Chelsea.
Hänggi, P., and Thomas, H. (1977) Time Evolution, Correlations and Linear Response of Non-Markov Processes, Zeitschr. für Physik B26, 85.
Lucas, R.E. (1972) Expectations and the Neutrality of Money, J. Economic Theory 4, 103.
Mandelbrot, B. (1966) Forecasts of Future Prices, Unbiased Markets and Martingale Models, J. Business 39, 242.
Kindleberger, C.P. (1996) Manias, Panics, and Crashes, A History of Financial Crises, New York: Wiley.
McCann., C.R. Jr (1994) Probability Foundations of Economic Theory, London: Routledge.
McCauley, J.L. (2008a) Time vs. Ensemble Averages for Nonstationary Time Series, Physica A387, 5188.
McCauley, J.L. (2008b) Nonstationarity of Efficient Financial Markets: FX Market Evolution from Stability to Instability, Int. Rev. Fin. An. 17, 820.
McCauley, J.L. (2009) Dynamics of Markets: The New Financial Economics, Cambridge: Cambridge University Press.
McCauley, J.L. (2010) NonMarkov Ito processes with 1-state memory, Physics Procedia 3, 1659.
McKay, C. (1980) Extraordinary Popular Delusions and the Madness of Crowds, New York: Harmony Books.
Muth, J.F. (1961) Rational Expectations and the Theory of Price Movements, Econometrica 29, 315.
Osborne, M.F.M. (1964) Brownian motion in the stock market, in: The Random Character of Stock Market Prices, P. Cootner (ed.), Cambridge MA: MIT Press.
Sargent, T.J. (1987) Macroeconomic Theory, New York: Academic Press.
Seemann, L., McCauley, J.L., and Gunaratne, G.H. (2011) Intraday Volatility and Scaling in High Frequency Foreign Exchange Markets, Int. Rev. Fin. An. 20, 121.
Stratonovich, R.L. (1963) Topics in the Theory of Random Noise, tr. by R. A. Silverman, New York: Gordon & Breach.
The Trillion Dollar Bet (no date), http://www.pbs.org/wgbh/nova/stockmarket/.