6	Much ado about knotting Euler’s Formula for Polyhedra

 

 

What does it say?

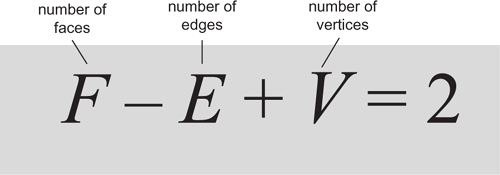
The numbers of faces, edges, and vertices of a solid are not independent, but are related in a simple manner.

Why is that important?

It distinguishes between solids with different topologies using the earliest example of a topological invariant. This paved the way to more general and more powerful techniques, creating a new branch of mathematics.

What did it lead to?

One of the most important and powerful areas of pure mathematics: topology, which studies geometric properties that are unchanged by continuous deformations. Examples include surfaces, knots, and links. Most applications are indirect, but its influence behind the scenes is vital. It helps us understand how enzymes act on DNA in a cell, and why the motion of celestial bodies can be chaotic.