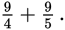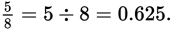
Chapter 10
Consecutive numbers: Numbers of a certain type, following one another without interruption. Numbers may be consecutive in ascending or descending order. The GRE prefers to test consecutive integers (e.g., −2, −1, 0, 1, 2, 3, . . . ), but you may encounter other types of consecutive numbers. For example:
−4, −2, 0, 2, 4, 6, . . . is a series of consecutive even numbers.
−3, 0, 3, 6, 9, . . . is a series of consecutive multiples of 3.
2, 3, 5, 7, 11, . . . is a series of consecutive prime numbers.
Cube: A number raised to the 3rd power. For example 43 = (4)(4)(4) = 64, showing that 64 is the cube of 4.
Decimal: A fraction written in decimal system format. For example, 0.6 is a decimal. To convert a fraction to a decimal, divide the numerator by the denominator. For instance,
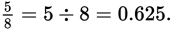
Decimal system: A numbering system based on the powers of 10. The decimal system is the only numbering system used on the GRE. Each figure, or digit, in a decimal number occupies a particular position, from which it derives its place value.
Denominator: The quantity in the bottom of a fraction, representing the whole.
Difference: The result of subtraction.
Digit: One of the numerals 0, 1, 2, 3, 4, 5, 6, 7, 8, or 9. A number can have several digits. For example, the number 542 has three digits: a 5, a 4, and a 2. The number 321,321,000 has nine digits but only four distinct (different) digits: 3, 2, 1, and 0.
Distinct: Different from each other. For example, 12 has three prime factors (2, 2, and 3) but only 2 distinct factors (2 and 3).
Element: One of the members of a set.
Exponent: The number that denotes the power to which another number or variable is raised. The exponent is typically written as a superscript to a number. For example, 53 equals (5)(5)(5). The exponent is also occasionally referred to as a “power.” For example, 53 can be described as “5 to the 3rd power.” The product, 125, is “the 3rd power of 5.” Exponents may be positive or negative integers or fractions, and they may include variables.
Fraction: The division of a part by a whole.
For example,
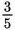is a fraction.
Integer: A number without fractional or decimal parts, including positive and negative whole numbers and zero. All integers are multiples of 1. The following are examples of integers: −5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5.
Number Line: A straight line, extending infinitely in either direction, on which numbers are represented as points. The number line below shows the integers from −3 to 4. Decimals and fractions can also be depicted on a number line, as can irrational numbers, such as
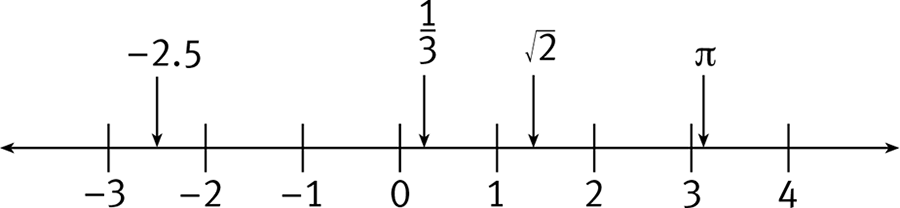
The values of numbers get larger as you move to the right along the number line. Numbers to the right of zero are positive; numbers to the left of zero are negative. Zero is neither positive nor negative. Any positive number is larger than any negative number. For example, −300 < 4.
Numerator: The quantity in the top of a fraction, representing the part.
Operation: A function or process performed on one or more numbers. The four basic arithmetic operations are addition, subtraction, multiplication, and division.
Part: A specified number of the equal sections that compose a whole.
Product: The result of multiplication.
Sequence: Lists that have an infinite number of terms, in order. The terms of a sequence are often indicated by a letter with a subscript indicating the position of the number in the sequence. For instance, a3 denotes the third number in a sequence, while an indicates the nth term in a sequence.
Set: A well-defined collection of items, typically numbers, objects, or events. The bracket symbols { } are normally used to define sets of numbers. For example, {2, 4, 6, 8} is a set of numbers.
Square: The product of a number multiplied by itself. A squared number has been raised to the 2nd power. For example, 42 = (4)(4) = 16, and 16 is the square of 4.
Sum: The result of addition.
Whole: A quantity that is regarded as a complete unit.
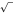square root
There are certain mathematical laws governing the results of the four basic operations: addition, subtraction, multiplication, and division. Although you won’t need to know the names of these laws for the GRE, you’ll benefit from understanding them.
A string of operations must be performed in proper order. The acronym PEMDAS stands for the correct order of operations:
If you have trouble remembering PEMDAS, you can think of the mnemonic “Please Excuse My Dear Aunt Sally.”
Example:
66 (3 − 2) ÷ 11
If you were to perform all the operations sequentially from left to right, without using PEMDAS, you would arrive at an answer of
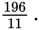But if you perform the operation within the parentheses first, you get 66(1) ÷ 11 = 66 ÷ 11 = 6, which is the correct answer.
Example:
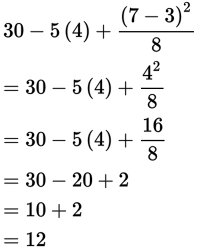
Addition and multiplication are both commutative, which means that switching the order of any two numbers being added or multiplied together does not affect the result.
Example:
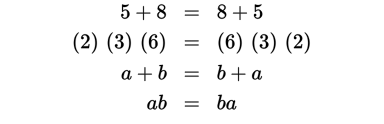
Division and subtraction are not commutative; switching the order of the numbers changes the result. For instance, 3 − 2 ≠ 2 − 3; the left side yields a difference of 1, while the right side yields a difference of −1. Similarly,
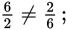the left side equals 3, while the right side equals
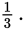
Addition and multiplication are also associative; regrouping the numbers does not affect the result.
Example:
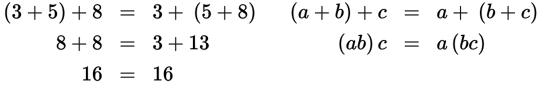
The distributive law of multiplication allows you to “distribute” a factor over numbers that are added or subtracted. You do this by multiplying that factor by each number in the group.
Example:
The law works for the numerator in division as well.
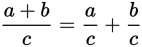
However, when the sum or difference is in the denominator—that is, when you’re dividing by a sum or difference—no distribution is possible.
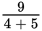is not equal to
