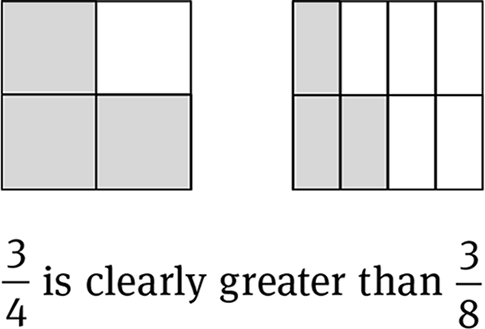
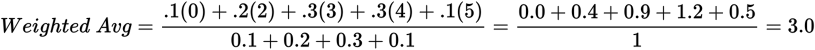The simplest way to understand the meaning of a fraction is to picture the denominator as the number of equal parts into which a whole unit is divided. The numerator represents a certain number of those equal parts.
On the left, the shaded portion is one of two equal parts that make up the whole. On the right, the shaded portion is three of four equal parts that make up the whole.
The fraction bar is interchangeable with a division sign. You can divide the numerator of a fraction by the denominator to get an equivalent decimal. However, the numerator and denominator must each be treated as a single quantity.
Example:
Evaluate
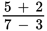
You can’t just rewrite the fraction as 5 + 2 ÷ 7 − 3, because the numerator and the denominator are each considered distinct quantities. Instead, you would rewrite the fraction as (5 + 2) ÷ (7 − 3). The order of operations (remember PEMDAS?) tells us that operations in parentheses must be performed first.
That gives you 7 ÷ 4. Your final answer would be
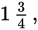or 1.75, depending on the form of the answer choices.
Since multiplying or dividing a number by 1 does not change the number, multiplying the numerator and denominator of a fraction by the same nonzero number doesn’t change the value of the fraction—it’s the same as multiplying the entire fraction by 1.
Example:
Change
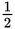into an equivalent fraction with a denominator of 4.
To change the denominator from 2 to 4, you’ll have to multiply it by 2. But to keep the value of the fraction the same, you’ll also have to multiply the numerator by 2.
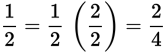
Similarly, dividing the numerator and denominator by the same nonzero number leaves the value of the fraction unchanged.
Example:
Change
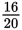into an equivalent fraction with a denominator of 10.
To change the denominator from 20 to 10, you’ll have to divide it by 2. But to keep the value of the fraction the same, you’ll have to divide the numerator by the same number.
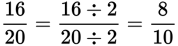
Most fractions on the GRE are in lowest terms. That means that the numerator and denominator have no common factor greater than 1.
For example, the final answer of
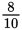that we obtained in the previous example was not in lowest terms, because both 8 and 10 are divisible by 2. In contrast, the fraction
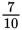is in lowest terms, because there is no factor greater than 1 that 7 and 10 have in common. To convert a fraction to its lowest terms, we use a method called reducing, or canceling. To reduce, simply divide any common factors out of both the numerator and the denominator.
Example:
Reduce
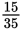to lowest terms.
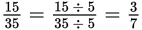(because a 5 cancels out, top and bottom)
Sometimes it may be necessary to repeat the process and keep dividing out common factors until no common factor greater than 1 remains for the numerator and denominator.
Example:
Reduce
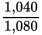to lowest terms.
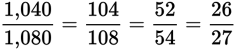
You cannot add or subtract fractions unless they have the same denominator. If they don’t, you’ll have to convert each fraction to an equivalent fraction with the least common denominator. Then add or subtract the numerators (not the denominators!) and, if necessary, reduce the resulting fraction to its lowest terms.
Given two fractions with different denominators, the least common denominator is the least common multiple of the two denominators, that is, the smallest number that is evenly divisible by both denominators.
Example:
What is the least common denominator of
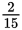and
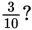
The least common denominator of the two fractions will be the least common multiple of 15 and 10.
Because 15 = (5)(3) and 10 = (5)(2), the least common multiple of the two numbers is (5)(3)(2), or 30. That makes 30 the least common denominator of
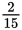and
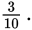
Example:
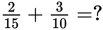
As we saw in the previous example, the least common denominator of the two fractions is 30. Change each fraction to an equivalent fraction with a denominator of 30.
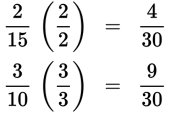
Then add:
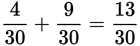
Since 13 and 30 have no common factor greater than 1,
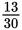is in lowest terms. You can’t reduce it further.
To multiply fractions, multiply the numerators and multiply the denominators.
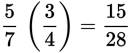
Multiplying numerator by numerator and denominator by denominator is simple. But it’s easy to make careless errors if you have to multiply a string of fractions or work with large numbers. You can minimize those errors by reducing before you multiply.
Example:
Multiply
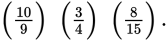
First, cancel a 5 out of the 10 and the 15, a 3 out of the 3 and the 9, and a 4 out of the 8 and the 4:
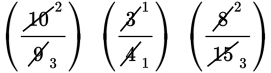
Then multiply numerators together and denominators together:
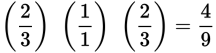
To get the reciprocal of a common fraction, turn the fraction upside-down so that the numerator becomes the denominator, and vice versa. If a fraction has a numerator of 1, the fraction’s reciprocal will be equivalent to an integer.
Example:
What is the reciprocal of
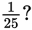
Inverting the fraction gives you the reciprocal,
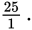But dividing a number by 1 doesn’t change the value of the number.
Since
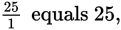the reciprocal of
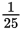equals 25.
To divide fractions, multiply by the reciprocal of the number or fraction that follows the division sign.
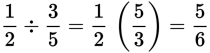
(The operation of division produces the same result as multiplication by the inverse.)
Example:
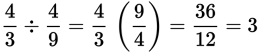
Given two positive fractions with the same denominator, the fraction with the larger numerator will have the larger value.
Example:
Which is greater,
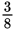or
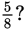
But if you’re given two positive fractions with the same numerator but different denominators, the fraction with the smaller denominator will have the larger value.
Example:
Which is greater,
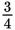or
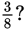
The diagrams below show two wholes of equal size. The one on the left is divided into 4 equal parts, 3 of which are shaded. The one on the right is divided into 8 equal parts, 3 of which are shaded.
If neither the numerators nor the denominators are the same, you have three options. You can turn both fractions into their decimal equivalents. Or you can express both fractions in terms of some common denominator and then see which new equivalent fraction has the largest numerator. Or you can cross multiply the numerator of each fraction by the denominator of the other. The greater result will wind up next to the greater fraction.
Example:
Which is greater,
or
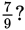
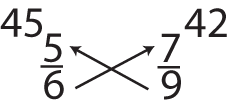
Since
A mixed number consists of an integer and a fraction.
An improper fraction is a fraction whose numerator is greater than its denominator. To convert an improper fraction to a mixed number, divide the numerator by the denominator. The number of “whole” times that the denominator goes into the numerator will be the integer portion of the improper fraction; the remainder will be the numerator of the fractional portion.
Example:
Convert
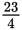to a mixed number.
Dividing 23 by 4 gives you 5 with a remainder of 3, so
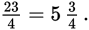
To change a mixed number to a fraction, multiply the integer portion of the mixed number by the denominator and add the numerator. This new number is your numerator. The denominator will not change.
Example:
Convert
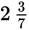to a fraction.
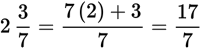
The reciprocal of a fraction between 0 and 1 is greater than both the original fraction and 1.
Example:
The reciprocal of
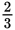is
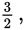which is greater than both 1 and
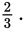
The reciprocal of a fraction between −1 and 0 is less than both the original fraction and −1.
Example:
The reciprocal of
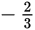is
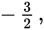or
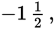which is less than both −1 and
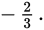
The square of a fraction between 0 and 1 is less than the original fraction.
Example:
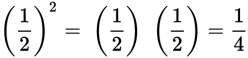
But the square of any fraction between 0 and −1 is greater than the original fraction, because multiplying two negative numbers gives you a positive product and any positive number is greater than any negative number.
Example:
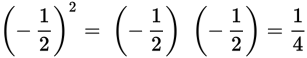
Multiplying any positive number by a fraction between 0 and 1 gives a product smaller than the original number.
Example:
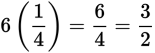
Multiplying any negative number by a fraction between 0 and 1 gives a product greater than the original number.
Example:
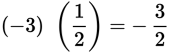
It’s easy to convert decimals to common fractions, and vice versa. Any decimal fraction is equivalent to some common fraction with a power of 10 in the denominator.
To convert a decimal between 0 and 1 to a fraction, determine the place value of the last nonzero digit and set that value as the denominator. Then use all the digits of the decimal number as the numerator, ignoring the decimal point. Finally, if necessary, reduce the fraction to its lowest terms.
Example:
Convert 0.875 to a fraction in lowest terms.
The last nonzero digit is the 5, which is in the thousandths place. So the denominator of the common fraction will be 1,000. The numerator will be 875:
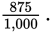
(You can ignore the zero to the left of the decimal point, since there are no nonzero digits to its left; it’s just a “placeholder.”)
Both 875 and 1,000 contain a factor of 25. Canceling it out leaves you with
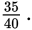Reducing that further by a factor of 5 gives you
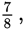which is in lowest terms.
To convert a fraction to a decimal, simply divide the numerator by the denominator.
Example:
What is the decimal equivalent of
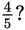
4 ÷ 5 = 0.8
Knowing place values allows you to assess the relative values of decimals.
Example:
Which is greater, 0.254 or 0.3?
Of course, 254 is greater than 3. But
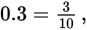which is equivalent to
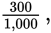while 0.254 is equivalent to only
Since
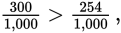0.3 is greater than 0.254.
Here’s the simplest way to compare decimals: add zeros after the last digit to the right of the decimal point in each decimal fraction until all the decimals you’re comparing have the same number of digits. Essentially, what you’re doing is giving all the fractions the same denominator so that you can just compare their numerators.
Example:
Arrange in order from smallest to largest: 0.7, 0.77, 0.07, 0.707, and 0.077.
The numbers 0.707 and 0.077 end at the third place to the right of the decimal point—the thousandths place. Add zeros after the last digit to the right of the decimal point in each of the other fractions until you reach the thousandths place:
Therefore, 0.07 < 0.077 < 0.7 < 0.707 < 0.77.
You should be familiar and comfortable with the practice of “rounding off” numbers. To round off a number to a particular place, look at the digit immediately to the right of that place. If the digit is 0, 1, 2, 3, or 4, don’t change the digit that is in the place to which you are rounding. If it is 5, 6, 7, 8, or 9, change the digit in the place to which you are rounding to the next higher digit. Replace all digits to the right of the place to which you are rounding with zeros.
For example, to round off 235 to the tens place, look at the units place. Since it is occupied by a 5, you’ll round the 3 in the tens place up to a 4, giving you 240. If you had been rounding off 234, you would have rounded down to the existing 3 in the tens place; that would have given you 230.
Example:
Round off 675,978 to the hundreds place.
The 7 in the tens place means that you will have to round the hundreds place up. Since there is a 9 in the hundreds place, you’ll have to change the thousands place as well. Rounding 675,978 to the hundreds place gives you 676,000.
Rounding off large numbers before calculation will allow you to quickly estimate the correct answer.
Estimating can save you valuable time on many GRE problems. But before you estimate, check the answer choices to see how close they are. If they are relatively close together, you’ll have to be more accurate than if they are farther apart.
The word percent means “hundredths,” and the percent sign, %, means
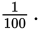For example, 25% means
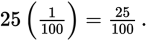(Like the division sign, the percent sign evolved from the fractional relationship; the slanted bar in a percent sign represents a fraction bar.)
Percents measure a part-to-whole relationship with an assumed whole equal to 100. The percent relationship can be expressed as
For example, if
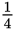of a rectangle is shaded, the percent of the rectangle that is shaded is
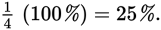
Like fractions, percents express the relationship between a specified part and a whole; more specifically, percents express a relationship of a part out of 100. Thus, 25%,
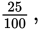and 0.25 are simply different names for the same part-whole relationship.
On the GRE, many fractions and percents appear in word problems. You’ll solve the problems by plugging the numbers you’re given into some variation of one of the three basic formulas:
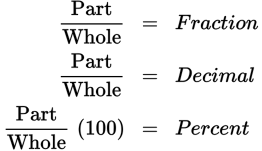
To avoid careless errors, look for the key words is and of. Is (or are) often introduces the part, while of almost invariably introduces the whole.
Since the percent sign means
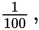100% means
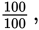or one whole. The key to solving some GRE percent problems is to recognize that all the parts add up to one whole: 100%.
Example:
All 1,000 registered voters in Smithtown are Democrats, Republicans, or independents. If 75% of the registered voters are Democrats and 5% are independents, how many are Republicans?
We calculate that 75% + 5%, or 80% of the 1,000 registered voters, are either Democrats or independents. The three political affiliations together must account for 100% of the voters; thus, the percentage of Republicans must be 100% − 80%, or 20%. Therefore, the number of Republicans must be 20% of 1,000, which is 20% (1,000), or 200.
Multiplying or dividing a number by 100% is just like multiplying or dividing by 1; it doesn’t change the value of the original number.
To change a fraction to its percent equivalent, multiply by 100%.
Example:
What is the percent equivalent of
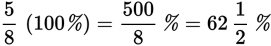
To change a decimal fraction to a percent, you can use the rules for multiplying by powers of 10. Move the decimal point two places to the right and insert a percent sign.
Example:
What is the percent equivalent of 0.17?
To change a percent to its fractional equivalent, divide by 100%.
Example:
What is the common fraction equivalent of 32%?
To convert a percent to its decimal equivalent, use the rules for dividing by powers of 10—just move the decimal point two places to the left.
Example:
What is the decimal equivalent of 32%?
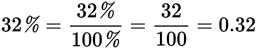
When you divide a percent by another percent, the percent sign “drops out,” just as you would cancel out a common factor.
Example:
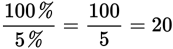
Translation: There are 20 groups of 5% in 100%.
But when you divide a percent by a regular number (not by another percent), the percent sign remains.
Example:
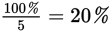
Translation: One-fifth of 100% is 20%.
As you can see, changing percents to fractions, or vice versa, is pretty straightforward. But it does take a second or two that you might spend more profitably doing other computations or setting up another GRE math problem. Familiarity with the following common equivalents will save you time.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
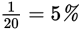
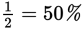
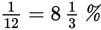
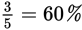
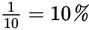
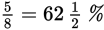
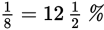
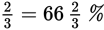
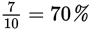
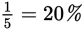
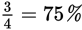
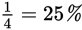
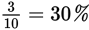
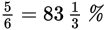
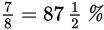
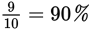
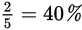
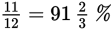
You can solve most percent problems by plugging the given data into the percent formula:
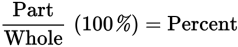
Most percent problems give you two of the three variables and ask for the third.
Example:
Ben spends $30 of his annual gardening budget on seed. If his total annual gardening budget is $150, what percentage of his budget does he spend on seed?
This problem specifies the whole ($150) and the part ($30) and asks for the percentage. Plugging those numbers into the percent formula gives you this:
Ben spends 20% of his annual gardening budget on seed.
When the GRE tests percent increase or decrease, use the formula:
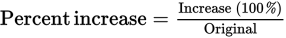
or
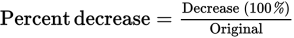
To find the increase or decrease, just take the difference between the original and the new. Note that the “original” is the base from which change occurs. It may or may not be the first number mentioned in the problem.
Example:
Two years ago, 450 seniors graduated from Inman High School. Last year, 600 seniors graduated. By what percent did the number of graduating seniors increase?
The original is the figure from the earlier time (two years ago): 450. The increase is 600 − 450, or 150. So the percent increase is
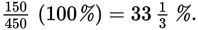
Example:
If the price of a $120 dress is increased by 25%, what is the new selling price?
To find the new whole, you’ll first have to find the amount of increase. The original whole is $120, and the percent increase is 25%. Plugging in, we find that:
The amount of increase is $30, so the new selling price is $120 + $30, or $150.
On some difficult problems, you’ll be asked to find more than one percent or to find a percent of a percent. Be careful: You can’t add percents of different wholes.
Example:
The price of an antique is reduced by 20 percent, and then this price is reduced by 10 percent. If the antique originally cost $200, what is its final price?
The most common mistake in this kind of problem is to reduce the original price by a total of 20% + 10%, or 30%. That would make the final price 70 percent of the original, or 70% ($200) = $140. This is not the correct answer. In this example, the second (10%) price reduction is taken off of the first sale price—the new whole, not the original whole.
To get the correct answer, first find the new whole. You can find it by calculating either $200 − (20% of $200) or 80% ($200). Either way, you will find that the first sale price is $160. That price then has to be reduced by 10%. Either calculate $160 − (10% ($160)) or 90% ($160). In either case, the final price of the antique is $144.
Certain types of percent problems lend themselves readily to the alternative technique of Picking Numbers. These include problems in which no actual values are mentioned, just percents. If you assign values to the percents you are working with, you’ll find the problem less abstract.
You should almost always pick 100 in percent problems, because it’s relatively easy to find percentages of 100.
Example:
The price of a share of company A’s stock fell by 20 percent two weeks ago and by another 25 percent last week to its current price. By what percent of the current price does the share price need to rise in order to return to its original price?
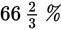
Pick a value for the original price of the stock. Since this is a percent question, picking $100 will make the math easy. The first change in the price of the stock was by 20% of $100, or $20, making the new price $100 − $20 = $80.
The price then fell by another 25%. You know that 25% is the same as
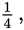and
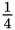of $80 is $20. Therefore, the current price is $80 − $20 = $60. To return to its original price, the stock needs to rise from $60 to $100, that is, by $100 − $60 = $40. Then $40 is what percent of the current price, $60?
Percent problems are often presented as word problems. We have already seen how to identify the percent, the part, and the whole in simple percent word problems. Here are some other terms that you are likely to encounter in more complicated percent word problems:
Profit made on an item is the seller’s price minus the cost to the seller. If a seller buys an item for $10 and sells it for $12, he has made $2 profit. The percent of the selling price that is profit is as follows:
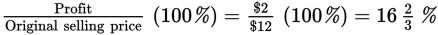
A discount on an item is the original price minus the reduced price. If an item that usually sells for $20 is sold for $15, the discount is $5. A discount is often represented as a percentage of the original price. In this case, the
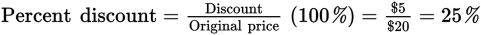
The sale price is the final price after discount or decrease.
Occasionally, percent problems will involve interest. Interest is given as a percent per unit of time, such as 5% per month. The sum of money invested is the principal. The most common type of interest you will see is simple interest. In simple interest, the interest payments received are kept separate from the principal.
Example:
If an investor invests $100 at 20% simple annual interest, how much does she have at the end of three years?
The principal of $100 yields 20% interest every year. Because 20% of $100 is $20, after three years the investor will have three years of interest, or $60, plus the principal, for a total of $160.
In compound interest, the money earned as interest is reinvested. The principal grows after every interest payment received.
Example:
If an investor invests $100 at 20% compounded annually, how much does he have at the end of 3 years?
The first year the investor earns 20% of $100 = $20. So, after one year, he has $100 + $20 = $120.
The second year the investor earns 20% of $120 = $24. So, after two years, he has $120 + $24 = $144.
The third year the investor earns 20% of $144 = $28.80. So, after three years, he has $144 + $28.80 = $172.80.
A ratio is the proportional relationship between two quantities. The ratio, or relationship, between two numbers (for example, 2 and 3) may be expressed with a colon between the two numbers (2:3), in words (“the ratio of 2 to 3”), or as a fraction
To translate a ratio in words to numbers separated by a colon, replace to with a colon.
To translate a ratio in words to a fractional ratio, use whatever follows the word of as the numerator and whatever follows the word to as the denominator. For example, if we had to express the ratio of glazed doughnuts to chocolate doughnuts in a box of doughnuts that contained 5 glazed and 7 chocolate doughnuts, we would do so as
Note that the fraction
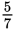does not mean that
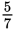of all the doughnuts are glazed doughnuts. There are 5 + 7, or 12 doughnuts altogether, so of the doughnuts,
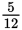are glazed. The
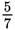ratio merely indicates the proportion of glazed to chocolate doughnuts. For every five glazed doughnuts, there are seven chocolate doughnuts.
Treating ratios as fractions can make computation easier. Like fractions, ratios often require division. And, like fractions, ratios ultimately should be reduced to lowest terms.
Example:
Joe is 16 years old, and Mary is 12 years old. Express the ratio of Joe’s age to Mary’s age in lowest terms.
The ratio of Joe’s age to Mary’s age is
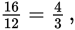or 4:3.
In a part:whole ratio, the “whole” is the entire set (for instance, all the workers in a factory), while the “part” is a certain subset of the whole (for instance, all the female workers in the factory).
In GRE ratio question stems, the word fraction generally indicates a part:whole ratio. “What fraction of the workers are female?” means “What is the ratio of the number of female workers to the total number of workers?”
Example:
The sophomore class at Milford Academy consists of 15 boys and 20 girls. What fraction of the sophomore class is female?
The following three statements are equivalent:
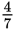of the sophomores are female.Ratios are usually reduced to their simplest form (that is, to lowest terms). If the ratio of men to women in a room is 5:3, you cannot necessarily infer that there are exactly five men and three women.
If you knew the total number of people in the room, in addition to the male-to-female ratio, you could determine the number of men and the number of women in the room. For example, suppose you know that there are 32 people in the room. If the male-to-female ratio is 5 to 3, then the ratio of males to the total is 5:(5 + 3), which is 5:8. You can set up an equation as
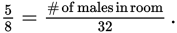Solving, you will find that the number of males in the room is 20.
Example:
The ratio of domestic sales revenues to foreign sales revenues of a certain product is 3:5. What fraction of the total sales revenues comes from domestic sales?
At first, this question may look more complicated than the previous example. You have to convert from a part:part ratio to a part:whole ratio (the ratio of domestic sales revenues to total sales revenues). And you’re not given actual dollar figures for domestic or foreign sales. But since all sales are either foreign or domestic, “total sales revenues” must be the sum of the revenues from domestic and foreign sales. You can convert the given ratio to a part:whole ratio because the sum of the parts equals the whole.
Although it’s impossible to determine dollar amounts for the domestic, foreign, or total sales revenues from the given information, the 3:5 ratio tells you that of every $8 in sales revenues, $3 comes from domestic sales and $5 from foreign sales. Therefore, the ratio of domestic sales revenues to total sales revenues is 3:8, or
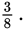
You can convert a part:part ratio to a part:whole ratio (or vice versa) only if there are no missing parts and no overlap among the parts—that is, if the whole is equal to the sum of the parts.
Example:
In a certain bag, the ratio of the number of red marbles to the number of blue marbles is 3:5. If there are only red and blue marbles in the bag, what is the ratio of the number of red marbles to the total number of marbles?
In this case, you can convert a part-to-part ratio (red marbles to blue marbles) to a part-to-whole ratio (red marbles to all marbles) because you know there are only red and blue marbles in the bag. The ratio of red marbles to the total number of marbles is 3:8.
Example:
Of the 25 people in Fran’s apartment building, there are 9 residents who use the roof only for tanning and 8 residents who use the roof only for gardening. The roof is only used by tanners and gardeners.
| Quantity A | Quantity B |
|---|---|
| The ratio of people who use the roof to total residents | 17:25 |
In this question, we do not know if there is any overlap between tanners and gardeners. How many, if any, residents do both activities? Since we don’t know, the relationship cannot be determined from the information given.
Most of the ratios that you’ll see on the GRE have two terms. But it is possible to set up ratios with more than two terms. These ratios express more relationships, and therefore convey more information, than do two-term ratios. However, most of the principles discussed so far with respect to two-term ratios are just as applicable to ratios of more than two terms.
Example:
The ratio of x to y is 5:4. The ratio of y to z is 1:2. What is the ratio of x to z?
We want the y’s in the two ratios to equal each other, because then we can combine the x:y ratio and the y:z ratio to form the x:y:z ratio that we need to answer this question. To make the y’s equal, we can multiply the second ratio by 4. When we do so, we must perform the multiplication on both components of the ratio. Since a ratio is a constant proportion, it can be multiplied or divided by any number without losing its meaning, as long as the multiplication and division are applied to all the components of the ratio. In this case, we find that the new ratio for y to z is 4:8. We can combine this with the first ratio to find a new x to y to z ratio of 5:4:8. Therefore, the ratio of x to z is 5:8.
A rate is a special type of ratio. Instead of relating a part to the whole or to another part, a rate relates one kind of quantity to a completely different kind. When we talk about rates, we usually use the word per, as in “miles per hour,” “cost per item,” etc. Since per means “for one” or “for each,” we express the rates as ratios reduced to a denominator of 1.
The most commonly tested rate on the GRE is speed. This is usually expressed in miles or kilometers per hour. The relationship between speed, distance, and time is given by the formula
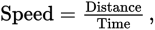which can be rewritten two ways:
and Distance = (Speed)(Time).
Anytime you can find two out of the three elements in this equation, you can find the third.
For example, if a car travels 300 miles in 5 hours, it has averaged
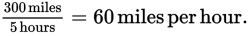(Note that speeds are usually expressed as averages because they are not necessarily constant. In this example, the car moved at an “average speed” of 60 miles per hour, but probably not at a constant speed of 60 miles per hour.)
Likewise, a rearranged version of the formula can be used to solve for missing speed or time.
Example:
How far do you drive if you travel for 5 hours at 60 miles per hour?
Example:
How much time does it take to drive 300 miles at 60 miles per hour?
Speed is not the only rate that appears on the GRE. For instance, you might get a word problem involving liters per minute or cost per unit. All rate problems, however, can be solved using the speed formula and its variants by conceiving of “speed” as “rate” and “distance” as “quantity.”
Example:
How many hours will it take to fill a 500-liter tank at a rate of 2 liters per minute?
Plug the numbers into our rate formula:
Now convert 250 minutes to hours: 250 minutes ÷ 60 minutes per hour =
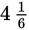hours to fill the tank. (As you can see from this problem, GRE Problem Solving questions test your ability to convert minutes into hours and vice versa. Pay close attention to what units the answer choice must use.)
In some cases, you should use proportions to answer rate questions.
Example:
If 350 widgets cost $20, how much will 1,400 widgets cost at the same rate?
Set up a proportion:
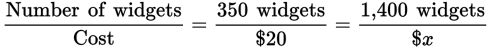
Solving, you will find that x = 80.
So, 1,400 widgets will cost $80 at that rate.
Rates can be added.
Example:
Nelson can mow 200 square meters of lawn per hour. John can mow 100 square meters of lawn per hour. Working simultaneously but independently, how many hours will it take Nelson and John to mow 1,800 square meters of lawn?
Add Nelson’s rate to John’s rate to find the combined rate.
200 meters per hour + 100 meters per hour = 300 meters per hour.
Divide the total lawn area, 1,800 square meters, by the combined rate, 300 square meters per hour, to find the number of required hours, 6.
The work formula can be used to find out how long it takes a number of people working together to complete a task. Let’s say we have three people. The first takes a units of time to complete the job, the second b units of time to complete the job, and the third c units of time. If the time it takes all three working together to complete the job is T, then
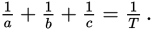
Example:
John can weed the garden in 3 hours. If Mary can weed the garden in 2 hours, how long will it take them to weed the garden at this rate, working independently?
Set John’s time per unit of work as a and Mary’s time per unit of work as b. (There is no need for the variable c, since there are only two people.) Plugging in, you find that
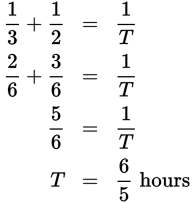
When there are only two people or machines in a combined work problem, we can use a simplified work formula.
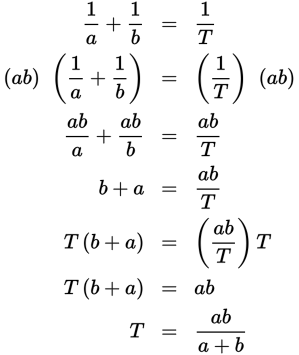
Here, a = the amount of time it takes person a to complete the job, and b = the amount of time it takes person b to complete the job.
Example:
Let’s use the same example from above: John takes 3 hours to weed the garden, and Mary takes 2 hours to weed the same garden. How long will it take them to weed the garden together?
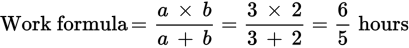
The average of a group of numbers is defined as the sum of the terms divided by the number of terms.
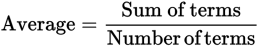
This equation can be rewritten two ways:
Thus, any time you have two out of the three values (average, sum of terms, number of terms), you can find the third.
Example:
Henry buys three items costing $2.00, $1.75, and $1.05. What is the average price (arithmetic mean) of the three items? (Don’t let the phrase arithmetic mean throw you; it’s just another term for average.)
Example:
June pays an average price of $14.50 for 6 articles of clothing. What is the total price of all 6 articles?
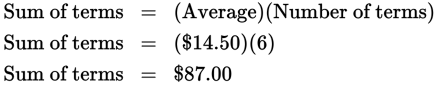
Example:
The total weight of the licorice sticks in a jar is 30 ounces. If the average weight of each licorice stick is 2 ounces, how many licorice sticks are there in the jar?
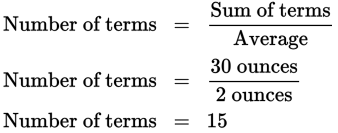
If you’re given the average, the total number of terms, and all but one of the actual numbers, you can find the missing number.
Example:
The average annual rainfall in Boynton for 1976−1979 was 26 inches per year. Boynton received 24 inches of rain in 1976, 30 inches in 1977, and 19 inches in 1978. How many inches of rainfall did Boynton receive in 1979?
You know that total rainfall equals 24 + 30 + 19 + (number of inches of rain in 1979).
You know that the average rainfall was 26 inches per year.
You know that there were 4 years.
So, plug these numbers into any of the three expressions of the average formula to find that Sum of terms = (Average)(Number of terms):
Another way to find a missing number is to understand that the sum of the differences between each term and the mean of the set must equal zero. Plugging in the numbers from the previous problem, for example, we find that:
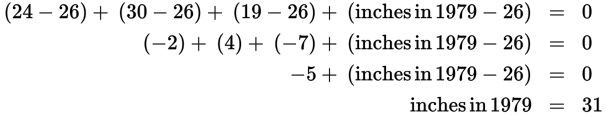
It may be easier to comprehend why this is true by visualizing a balancing, or weighting, process. The combined distance of the numbers above the average from the mean must be balanced with the combined distance of the numbers below the average from the mean.
Example:
The average of 63, 64, 85, and x is 80. What is the value of x?
Think of each value in terms of its position relative to the average, 80.
63 is 17 less than 80.
64 is 16 less than 80.
85 is 5 greater than 80.
So these three terms are a total of 17 + 16 − 5, or 28, less than the average. Therefore, x must be 28 greater than the average to restore the balance at 80. So x = 28 + 80 = 108.
When consecutive numbers are evenly spaced, the average is the middle value. For example, the average of consecutive integers 6, 7, and 8 is 7.
If there is an even number of evenly spaced numbers, there is no single middle value. In that case, the average is midway between (that is, the average of) the middle two values. For example, the average of 5, 10, 15, and 20 is 12.5, midway between the middle values 10 and 15.
Note that not all consecutive numbers are evenly spaced. For instance, consecutive prime numbers arranged in increasing order are not evenly spaced. But you can use the handy technique of finding the middle value whenever you have consecutive integers, consecutive odd or even numbers, consecutive multiples of an integer, or any other consecutive numbers that are evenly spaced.
When there is an equal number of terms in each set, and only when there is an equal number of terms in each set, you can average averages.
For example, suppose there are two bowlers and you must find their average score per game. One has an average score per game of 100, and the other has an average score per game of 200. If both bowlers bowled the same number of games, you can average their averages to find their combined average. Suppose they both bowled 4 games. Their combined average will be equally influenced by both bowlers. Hence, their combined average will be the average of 100 and 200. You can find this quickly by remembering that the quantity above the average and the quantity below the average must be equal. Therefore, the average will be halfway between 100 and 200, which is 150. Or, we could solve using our average formula:
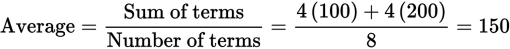
However, if the bowler with the average score of 100 had bowled 4 games and the bowler with the 200 average had bowled 16 games, the combined average would be weighted further toward 200 than toward 100 to reflect the greater influence of the 200 bowler than the 100 bowler upon the total. This is known as a weighted average.
Again, you can solve this by using the concept of a balanced average or by using the average formula.
Since the bowler bowling an average score of 200 bowled
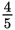of the games, the combined average will be
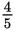of the distance along the number line between 100 and 200, which is 180. Or, you can plug numbers into an average formula to find the following:
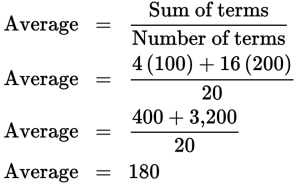
Example:
A teacher surprised her students with a 5 question pop quiz. 10% of the students answered no questions correctly, 20% had 2 right answers, 30% answered 3 questions correctly, 30% had 4 right answers and 10% had a perfect score. What was the weighted average of the number of correct answers?
