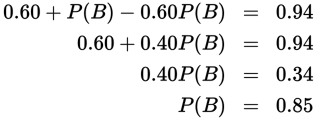
Sets are groups of values that have some common property, such as the negative odd integers greater than −10 or all positive integers that are evenly divisible by 3. The items in sets are called elements or members. If all the elements in a set can be counted, such as “the number of species of birds in North America,” that set is finite. If the elements in a set are limitless (e.g., “all positive numbers that are evenly divisible by 3”), that set is infinite. The set with no elements is called the empty set, which is represented by the symbol Ø. Logically, a set with any members is defined as nonempty. If all the elements of set A are among the elements of set B, then A is a subset of B. By definition, the empty set is a subset of all sets.
An important characteristic of sets is that elements are unique—that is, they are not repeated. For instance, the set of the numbers 1, 1, 2, 2, and 3 is {1, 2, 3}. Additionally, since order does not matter in sets, {1, 2, 3} is the same set as {3, 2, 1}.
A list is like a finite set except that the order of the elements matters and that duplicate members can be included. So 1, 2, 3 and 3, 2, 1 are different lists and 1, 2, 3, 2 is a valid list. Because order does matter in lists, elements can be uniquely identified by their position, such as “first element” or “fifth element.” Notice that sets are usually enclosed within the curly brackets, { and }, but lists are not.
The intersection of two sets is a set that consists of all the elements that are contained in both sets. (You can think of it as the overlap between the sets.) The intersection of sets A and B is written as A ∩ B. The union of two sets is the set of all the elements that are elements of either or both sets and is written as A ∪ B. If sets have no common elements, they are referred to as mutually exclusive, and their intersection is the empty set.
Drawing Venn diagrams is a helpful way to analyze the relationship among sets.
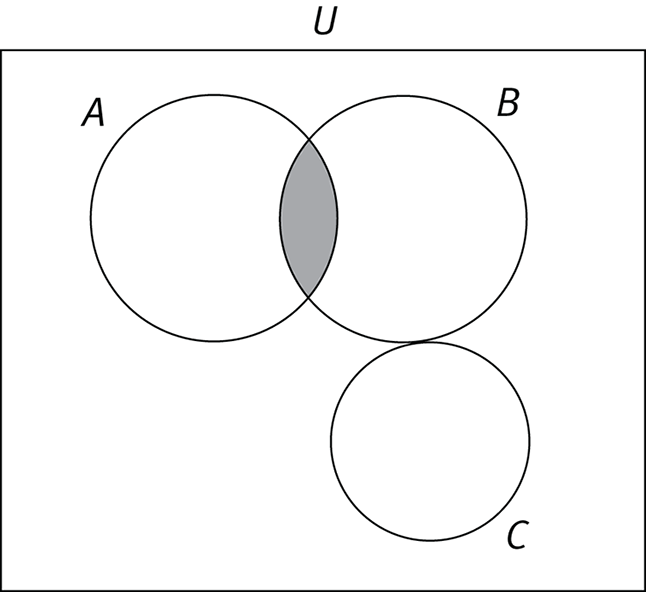
The set of all possible elements that have the characteristics of the sets represented by the circles in a Venn diagram is called a universal set and is represented by U. For instance, U could be the set of all species of birds in the world, A the set of species native to Europe, B those native to Asia, and C those native to Australia. In the diagram above, species from other continents are included within U but are not in any specific subset.
The inclusion-exclusion principle is a basic counting principle for sets. In the Venn diagram above, the shaded area represents A ∩ B (species native to both Europe and Asia), the elements that are within the intersection of A and B. Determining the number of elements in A ∪ B is a bit trickier. Merely adding the number of elements in A plus those in B is not correct because that would count the elements that show up in both sets twice. To find the number of elements in the union of two sets, use this formula:
This formula adjusts for the double-counting of elements that are in both sets. Notice that sets A and C are mutually exclusive, so |A ∩ C| = Ø. For the diagram above, |A ∪ C| = |A| + |C|.
When choices or events occur one after the other and the choices or events are independent of one another, the total number of possibilities is the product of the number of options for each. For example, if a ballot offers 3 candidate choices for Office A, 4 for Office B, and 2 for Office C, the total number of different ways that a voter could fill out the ballot is 3 × 4 × 2 = 24.
Occasionally, a GRE question may require a careful analysis of the number of options for each choice. If a website calls for a 3-letter password but no two letters can be the same, the total possibilities would be 26 × 25 × 24 = 15,600 because the stipulation that no two letters be the same reduces the number of choices for the second and third letters.
In situations where choices are “or” rather than “and,” as long as the two groups are mutually exclusive, add instead of multiplying. A menu has 3 choices for soup and 4 salad options; diners are permitted to select a soup or salad with their dinners. In this situation, the total number of choices available is 3 + 4 = 7.
A combination question asks you how many unordered subgroups can be formed from a larger group.
Some combination questions on the GRE can be solved without any computation just by counting or listing possible combinations.
Example:
Allen, Betty, and Claire must wash the dishes. They decide to work in shifts of two people. How many shifts will it take before all possible combinations have been used?
It is possible, and not time-consuming, to solve this problem by writing a list. Call Allen “A,” Betty “B,” and Claire “C.” There are three (AB, AC, BC) possible combinations.
Some combination questions use numbers that make quick, noncomputational solving difficult. In these cases, use the combination formula
where n is the number of items in the group as a whole and k is the number of items in each subgroup formed. The ! symbol means factorial (for example, 5! = (5)(4)(3)(2)(1) = 120).
Example:
The 4 finalists in a spelling contest win commemorative plaques. If there are 7 entrants in the spelling contest, how many possible groups of finalists are there?
Plug the numbers into the combination formula, such that n is 7 (the number in the large group) and k is 4 (the number of people in each subgroup formed).
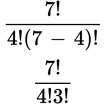
At this stage, it is helpful to reduce these terms. Since 7 factorial contains all the factors of 4 factorial, we can write 7! as (7)(6)(5)(4!) and then cancel the 4! in the numerator and denominator.
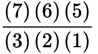
We can reduce further by crossing off the 6 in the numerator and the (3)(2) in the denominator.
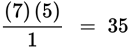
There are 35 potential groups of spelling contest finalists.
When you are asked to find potential combinations from multiple groups, multiply the potential combinations from each group.
Example:
How many groups can be formed consisting of 2 people from room A and 3 people from room B if there are 5 people in room A and 6 people in room B?
Insert the appropriate numbers into the combination formula for each room and then multiply the results. For room A, the number of combinations of 2 in a set of 5 is as follows:
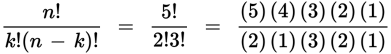
Reducing this, you get
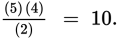For room B, the number of combinations of 3 in a set of 6 is as follows:
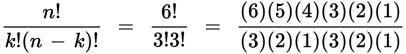
Reducing this, you get
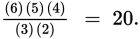
Multiply these to find that there are (10)(20) = 200 possible groups consisting of 2 people from room A and 3 people from room B.
Sometimes the GRE will ask you to find the number of possible subgroups when choosing one item from a set. In this case, the number of possible subgroups will always equal the number of items in the set.
Example:
Restaurant A has 5 appetizers, 20 main courses, and 4 desserts. If a meal consists of 1 appetizer, 1 main course, and 1 dessert, how many different meals can be ordered at restaurant A?
The number of possible outcomes from each set is the number of items in the set. So there are 5 possible appetizers, 20 possible main courses, and 4 possible desserts. The number of different meals that can be ordered is (5)(20)(4) = 400.
Within any group of items or people, there are multiple arrangements, or permutations, possible. For instance, within a group of three items (for example: A, B, C), there are six permutations (ABC, ACB, BAC, BCA, CAB, and CBA).
Permutations differ from combinations in that permutations are ordered. By definition, each combination larger than 1 has multiple permutations. On the GRE, a question asking “How many ways/arrangements/orders/schedules are possible?” generally indicates a permutation problem.
To find permutations, think of each place that needs to be filled in a particular arrangement as a blank space. The first place can be filled with any of the items in the larger group. The second place can be filled with any of the items in the larger group except for the one used to fill the first place. The third place can be filled with any of the items in the group except for the two used to fill the first two places, etc.
Example:
In a spelling contest, the winner will receive a gold medal, the second-place finisher will receive a silver medal, the third-place finisher will receive a bronze medal, and the fourth-place finisher will receive a blue ribbon. If there are 7 entrants in the contest, how many different arrangements of award winners are there?
The gold medal can be won by any of 7 people. The silver medal can be won by any of the remaining 6 people. The bronze medal can be won by any of the remaining 5 people. And the blue ribbon can be won by any of the remaining 4 people. Thus, the number of possible arrangements is (7)(6)(5)(4) = 840.
Probability measures the likelihood that an event will occur. Probability can be represented as a fraction, decimal, or percent. For example, if rain today is just as likely as not, then the probability of rain today can be expressed as
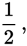0.5, or 50%. You may also see a probability expressed in everyday language: “one chance in a hundred” means the probability is
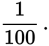Every probability is expressed as a number between 0 and 1 inclusive, with a probability of 0 meaning “no chance” and a probability of 1 meaning “guaranteed to happen.” The higher the probability, the greater the chance that an event will occur.
An event may include more than one outcome. For example, rolling an even number on a 6-sided die is the event that includes only the outcomes 2, 4, and 6. Many GRE probability questions are based on random experiments with a defined number of possible outcomes, such as drawing a random card from a full deck. If all the possible outcomes of the experiment are equally likely to occur, you can use this formula to calculate probability:
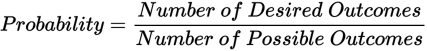
Example:
What is the probability of tossing a fair coin four consecutive times and having the coin land heads up exactly once?
Since a coin is tossed four times and each toss has two possible outcomes, the total number of outcomes, using the multiplication principle, is 2 × 2 × 2 × 2 = 24 = 16. The total number of desired outcomes can be easily counted: HTTT, THTT, TTHT, or TTTH. So there are 4 desired outcomes, and the probability of rolling exactly one head is
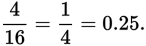
The total of the probabilities of all possible outcomes in an experiment must equal 1. For instance, the probability of a tossed coin landing heads up is
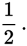The probability of the coin landing tails up is also
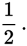There are no other possible outcomes, and
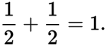By this same logic, if P(E) is the probability that an event will occur, then 1 − P(E) is the probability that the event will not occur. This is a useful fact in many probability questions.
Example:
What is the probability of tossing a fair coin four consecutive times and having the coin land heads up 0, 2, 3, or 4 times?
In the last example, we found that the probability of the coin landing heads up exactly once is 0.25. To find the probability of the coin landing heads up not exactly once, subtract that probability from 1: 1 − 0.25 = 0.75.
In many probability questions involving more than one event, the events are independent; one event does not affect the other. If the first toss of a fair coin results in a tail, the probability of the result of the second toss being a tail is still 0.5. In other cases the results are not independent. If there are 4 red disks and 4 green disks in a bag and 2 disks are withdrawn at random without replacement, the probability for the result of the second draw is dependent on the result of the first draw. If the first disk drawn is red, then only 3 red disks remain out of a total of 7, and the probability of drawing another red disk on the second draw is
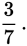If, however, the first draw is green, then 4 of the remaining 7 disks are red, and the probability of drawing red on the second draw is
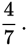
To calculate the probability of two or more independent events occurring, multiply the probabilities of the individual events. For example, the probability of rolling a 3 four consecutive times on a six-sided die would be
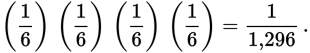
You can also calculate the probability of two or more dependent events occurring by multiplying their individual probabilities, but you must calculate the probability of each dependent event as if the preceding event had resulted in the desired outcome or outcomes.
Example:
A bag contains 10 marbles, 4 of which are blue and 6 of which are red. If 2 marbles are removed without replacement, what is the probability that both marbles removed are red?
The probability that the first marble removed will be red is
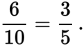The probability that the second marble removed will be red will not be the same, however. There will be fewer marbles overall, so the denominator will be one less. There will also be one fewer red marble. (Note that since we are asking about the odds of picking two red marbles, we are only interested in choosing a second marble if the first was red. Don’t concern yourself with situations in which a blue marble is chosen first.) If the first marble removed is red, the probability that the second marble removed will also be red is
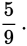So the probability that both marbles removed will be red is
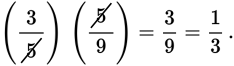
What about the probability of one or another event occurring? On the GRE, you can interpret “the probability of A or B” to mean “the probability of A or B or both,” and the formula for calculating this is similar to the inclusion-exclusion principle for sets described earlier in this chapter:
Example:
Events A and B are independent. P(A) is 0.60 and P(A or B) is 0.94. What is the probability that event B occurs?
Use the formula above: P(A or B) = P(A) + P(B) − P(A and B). Since the events are independent, P(A and B) = P(A) × P(B). Plug in the values given in the problem: 0.60 + P(B) − (0.60 × P(B)) = 0.94, then simplify:
