Answers and Explanations

Quantitative Reasoning 1

  1. C
    Right triangles ABD and CDB share a hypotenuse, segment DB. The shared hypotenuse should clue you to use the Pythagorean theorem. See that w and x are lengths of the legs of right triangle ABD; side AD has length w, side AB has length x. Also, y and z are lengths of the legs of right triangle CDB; side CD has length z, side CB has length y. Where a and b are lengths of the legs of a right triangle, and c is the length of the hypotenuse, a2 + b2 = c2. So here w2 + x2 = length BD2; y2 + z2 also equals length BD2. The quantities are equal, and the answer is (C).
  2. A
    You have x + 4y = 6 and x = 2y, and you want to compare x and y. Let’s start by finding y. Substitute 2y for x in the first equation and get 2y + 4y = 6 or 6y = 6. Divide both sides by 6 and get y = 1. If y = 1 and x = 2y, as the second equation states, x must equal 2. Because 2 is greater than 1, Quantity A is greater.
  3. C
    The problem doesn’t say how many employees work at the firm, so let’s pick a number. Since the problem involves percents, let’s pick 100 as the total number of employees.

    If there are 100 employees working at the firm, then one quarter of them, or 25, are managers. That leaves 75 employees, one-third of which, or 25, are assistants. Consequently, 100 − 25 − 25 = 50 employees are left to be technicians. Now check the quantities. Quantity A, the number of managers, is 25. Quantity B, half the number of technicians, is half of 50, which is also 25. Pick (C) the two quantities are equal.
  4. D

    To make the quantities look as much alike as you can, use FOIL to multiply out Quantity A. You’ll multiply a × b, 1 × b, 1 × a, and 1 × 1 and get ab + a + b + 1. Quantity B also has ab + 1. Quantity A has the additional terms a and b. There is no information given about possible values for a or b. Because a + b could be positive, negative, or zero, a relationship cannot be determined, and the answer is (D).

    You can also use Picking Numbers; let a = 1 and b = 2. Then Quantity A is (1 + 1)(2 + 1) = 6 and Quantity B is (1 × 2) + 1 = 3. In this case, Quantity A is greater. But if you let a = −1 and b = −2, you have Quantity A = (−1 + 1)(−2 + 1) = 0 and Quantity B = (−1 × −2) + 1 = 3. In this case, Quantity B is greater. You have demonstrated that a definite relationship cannot be determined, leading to answer choice (D).

  5. B
    In the two-digit number jk, the value of digit j is twice the value of digit k. You have to compare the value of k in Quantity A with 6 in Quantity B. If you plug in 6 for k, it is not possible to enter “twice the value of the digit k” for the digit j. That is because j can only be a single digit; it cannot be 12. In other words, k has to be something less than 6, so the answer must be (B). The value in Quantity B is greater.
  6. C
    Henry purchased x apples, and Jack purchased 10 apples less than one-third the number of apples Henry purchased. One-third of means the same as one-third times, and the number of apples Henry purchased is x. Thus, this boils down to 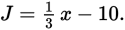You can plug this in for Quantity A. We have 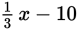in Quantity A and 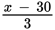in Quantity B. Now you can clear the fraction in Quantity B. Let’s split Quantity B into two fractions: 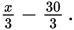Leave the 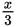alone and cancel the factor of 3 from the numerator and denominator of 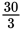and you’re left with 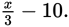What’s 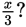It’s one-third of x. So Quantity A equals 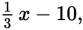while Quantity B also equals 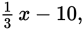and the answer is (C).
  7. A
    The figure shows a circle with diameter 8. The circumference of the circle is therefore 8π. Since the 90° central angle cuts a quarter of the circle, the length of arc QRS must likewise be a quarter of the circumference. Quantity A is therefore one-quarter of 8π, or 2π. Because π is a positive number, 2π must be greater than 2. Pick (A) Quantity A is greater.
  8. D
    You can suspect (D) because there is a range of possible values for the variables. In Quantity A, you have the volume of a rectangular solid with length 5 feet, width 4 feet, and height x feet. The formula is length times width times height, so the volume is 5 times 4 times x, or 20x.  The volume of Quantity B is therefore 10 times 8 times y, or 80y. If 4 < x < 6, then the range of values for Quantity A is 80 < V < 120. If 1 < y < 2, then the range of values for Quantity B is 80 < V < 160. Since the two ranges overlap, it’s possible that the two quantities are equal or that one is greater than the other. So, the correct answer is (D).
  9. B

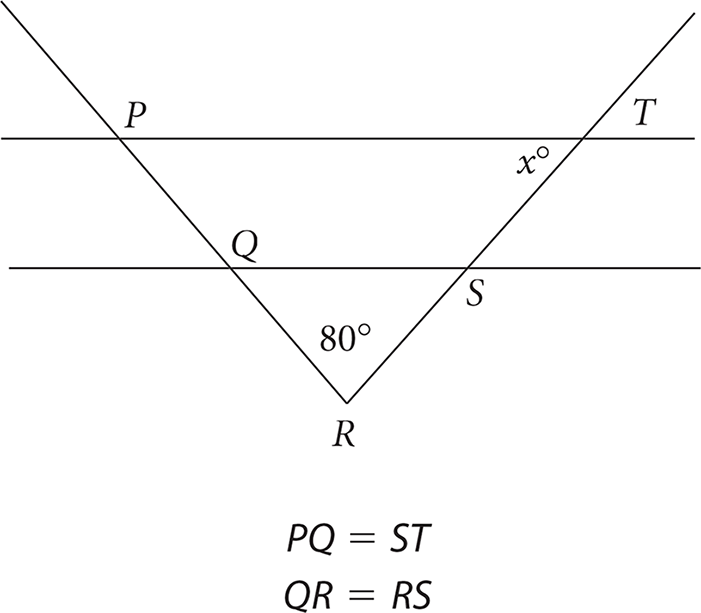
    The goal is to find x, the measure of one of the angles formed by the intersection of ST and PT. Now angle QRS is labeled 80°. You also know PQ and ST have the same length and QR and RS have the same length. If you add PQ and QR, you get PR. If you add ST and RS, you get RT. If you add equals to equals, you get equals, so PQ + QR must be the same as ST + RS, which means that PR and RT are the same. Thus, you have isosceles triangle PRT, and you’re given one angle that has measure 80 and a second angle that has measure x. The angle measuring x is opposite equal side PR. That means the other angle must have the same measure. The sum of the interior angles in a triangle always equals 180°. Thus, x + x + 80 must equal 180, 2x = 100, and x = 50. The answer is (B).

  10. 30
    This is a permutation problem because the order in which the duo is chosen matters. The producer has two slots to fill. For the lead role, there are 6 people to choose from. For the supporting role, there will be 5 people to choose from. So the number of possible duos is 6 × 5 = 30.
  11. E

    The question asks for the number of different dinners Jane could make. Since the order of the selections in the dinner doesn’t matter, this is a combination problem. But it involves three possible combination types: Veg, Meat, Meat; Veg, Veg, Meat; or Veg, Veg, Veg. We must calculate the possibilities for each type of combination and then add the results to find the total number of different combinations possible.

    Let V represent vegetarian and M represent meat.

    Then with V, M, M, she has 5 choices for the vegetarian (she must choose 1) × 4 choices for meat (she must choose 2).

    For V, V, M, she will choose 2 from among 5 for the vegetarian and 1 among 4 for the meat.

    If she goes with V, V, V, the all-vegetarian menu, she will choose a subgroup of 3 from among 5 vegetarian choices.

    If n and k are positive integers where n = k, then the number of different subgroups consisting of k objects that can be selected from a group consisting of n different objects, denoted by nCk, is given by the formula

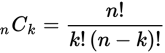
    Here the total number of different possible servings for a plate is (5C1)(4C2) + (5C2)(4C1) + (5C3).

    Now 5C1 represents choosing 1 type of vegetable selection from 5 different types, so 5C1 = 5. (The formula also gives this result.) Now we use the formula to find the next two combinations:

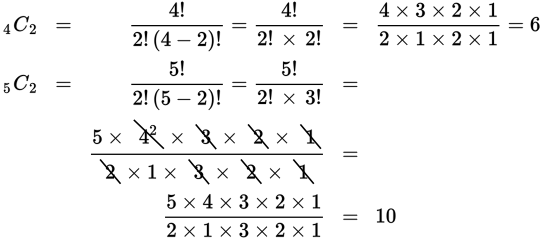
    Here 4C1 corresponds to choosing 1 type of meat selection from 4 different types, so 4C1 = 4. Then we use the formula again:

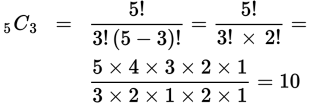
    So the number of different possible dinners of these three items is 5 × 6 + 10 × 4 + 10 = 80, choice (E).

  12. 6
    You could find the number of tasks per hour from one computer, but that would add extra steps, because you want to find out how many computers you need to do a certain number of tasks in three hours. Well, if the computer can do 30 tasks in six hours, it can do 15 tasks in three hours. So, two computers could complete 30 tasks in that time. Three computers could do 45; four could do 60; five could do 75; six could do 90. You can’t get by with five computers because you have to get 80 tasks done, so you’ll need 6 computers.
  13. C

    Picking Numbers is the best strategy, since there are variables in the question and the answer choices. If c = 3, then 2c = 6. There are two integers between 3 and 6, so plug c = 3 into the answer choices to see which one is equal to 2.

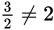
    2. 3 ≠ 2
    3. 3 − 1 = 2
    4. 3 − 2 ≠ 2
    5. 3 + 1 ≠ 2

    The only answer choice that equals 2 when c = 3 is (C), so (C) is correct.

  14. B, D
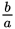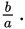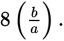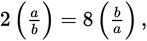    You’re asked to find what could be; that tells you there may be more than one possible value for You’re told the ratio of 2a to b is 8 times the ratio of b to a. That’s awkward to keep track of in English—it’s a little easier to write fractions. The ratio of 2a:b equals So, or 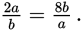Cross multiply to get 2a2 = 8b2, or a2 = 4b2. Multiply each side of the equation by 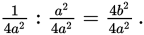This is the same as 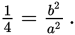Take the square root of both sides of the equation: 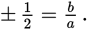The ratio of b to a is 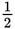or 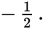So, (B) and (D) are the answers. This problem is also a great candidate for Backsolving, although since this question could have more than one correct answer, you would need to test all answer choices to see which ones work out.
  15. 8
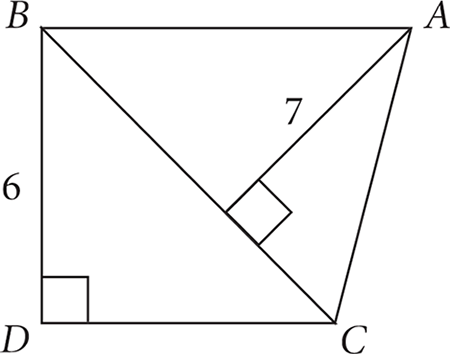
    Right triangle BDC and triangle ABC, where side BC is the common side of the two triangles. A height of 7 is drawn from vertex A to a point on line BC, and side BD from right triangle BDC is equal to 6.

    It is given that the area of triangle ABC is 35, and in the diagram, you’re given a height for triangle ABC. If you use BC as the base of the triangle, the triangle’s height is 7, so you can find the length of BC. The length BC, which is the base of triangle ABC, is also the hypotenuse of right triangle BDC. Given the hypotenuse and the length of leg BD, which is given in the diagram as 6, you’ll be able to find the third leg of the triangle, side DC, which is what you’re looking for.

    Going back to triangle ABC, the area is 35 and the height is 7. The area of a triangle is 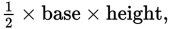so 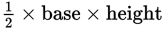is 35. Therefore, 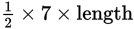BC is 35. That means 7 × length BC is 70, so BC must have length 10. Now look at right triangle BDC. Here is a right triangle with one leg of length 6, the hypotenuse of length 10, and the third side unknown. That’s one of the famous Pythagorean ratios—it’s a 3:4:5 triangle. So DC must have length 2 × 4, or 8.

  16. D
    First, find the value of m. You are told that 3m is 81. Well, 81 is 9 × 9 and 9 is 32. So you have 32 × 32 = 81 or 3 × 3 × 3 × 3 = 81. There are four factors of 3 in 81, so m has the value 4. Now 43 is 4 × 4 × 4 is 64. So (D) is correct. Note that (A) is a trap—that’s the value of m, not m3.
  17. D, E

    The problem states that x is between 0 and 1, so x must be a positive fraction (or decimal) less than 1. We can pick a number to get to the correct answer(s) here because both the question and the answer choices have variables. The decimal 0.5 is in the middle of the given range, so it’s a good starting point.

    (A) Incorrect. Doubling any positive value always produces a greater value, not a lesser value.

    (B) Incorrect. 2 × 0.5 = 1; a smaller fraction could make this statement true, but our correct answer(s) must always be true.

    (C) Incorrect. 2 × 0.5 = 1; a larger fraction could make this statement true, but our correct answer(s) must always be true.

    (D) Correct. 0.52 = 0.25; the square of any number between 0 and 1 (exclusive) will be less than the original number. This example illustrates that property.

    (E) Correct. 0.25 < 1; the square of any number between 0 and 1 (exclusive) will be less than 1. This is an example of that property. So, the correct answers are (D) and (E).

  18. C
    To find how many categories had energy use greater than 150 million kilowatt-hours, you have to find out how many total kilowatt-hours were used in that year using the line graph. You see that 600 million kilowatt-hours were used in 1995. What is the relationship of 150 million kilowatt-hours to 600 million kilowatt-hours? It’s 25% of 600 million kilowatt-hours, so you’re looking for categories with more than 25% of the energy use for 1995. How many categories exceeded 25%? Just two, government and industrial. So your answer is (C).
  19. C
    To find the per capita, or per person, personal energy use in Country Y in 2005, divide the personal energy use by the number of people. Since the question gives you the population—500 million people—you only need to find the personal energy use.

    According to the top graph, total energy use in 2005 was about 675 million kilowatt-hours. According to the bottom graph, personal energy use was about 20% of the total, or 675 × 0.20 = 135 million kilowatt-hours. Divide this number by the population of Country Y in 2005: 135 million kilowatt-hours divided by 500 million people = 0.27 kilowatt-hours per person, or choice (C).
  20. C, D

    Since this is an all-that-apply question, check each choice systematically.

    Choice (A): According to the bottom graph, energy for farm use decreased from 30% to 20% of the total between 1990 and 1995. Since 30 is 50% greater than 20, total energy use would have had to increase by at least 50% to compensate. The top graph shows that it did not, so choice (A) is incorrect.

    Choice (B): According to the bottom graph, energy for farm use decreased from 20% to a little more than 10% of the total between 1995 and 2000. Since 20 is double 10, total energy use would have had to nearly double in order to compensate—that definitely did not happen! Choice (B) is out.

    The bottom graph shows that energy for farm use, as a percentage of the total, increased from 2000 onward. Since total energy use increased every year, total farm energy use must have increased also. Thus, without any calculation, you know that choices (C) and (D) must be correct.