8
Buffett's Approach to Portfolio and Risk Management
“Rule No.1: Never lose money. Rule No.2: Never forget rule No.1.”
—Warren Buffett, Rules That Warren Buffett Lives By
Introduction
Putting all of your eggs (or investments) in one basket is too risky for nearly everyone. The basket could fall, breaking all of the eggs. Similarly, a specific stock could go bankrupt, potentially wiping out all, or a good portion, of the value of your investments. That's really taking the L. Even brand-name stocks such as Kodak, General Motors, Enron, WorldCom, and Lehman Brothers went bankrupt, taking their stock prices to $0. In Chapter 2, we mentioned that most people diversify their investments, or spread them across different assets. It's one of the fundamentals of investing for most people.
A portfolio is a basket of investments, but we'll mostly use the term diversified portfolio in this chapter and for the remainder of the book to describe what your overall, or aggregate, portfolio might look like. But how do you best diversify your investments, known in the investment world as selecting an optimal portfolio? There are several approaches, and—not surprisingly—Buffett has weighed in on the subject. Selecting a portfolio goes hand in hand with risk, since risk and return are two sides of the same coin. We emphasized this point back in Chapter 2, illustrated with the famous coin flipping example, the Saint Petersburg Paradox. And yes, Buffett has weighed in on risk too. In fact, one of his most humorous quotes is on risk. He said, “Rule No. 1: Never lose money. Rule No. 2: Never forget rule No. 1.”
Of course, you can't invest in something, other than an FDIC-insured bank product or a highly rated short-term government bond, and never lose money. But Buffett's quote makes it clear that investors should have a keen focus on risk before investing any money. That mindset merits a Tip.
To further show why it's important not to lose money, consider the following example on the difficulty of recovering from losses. If you start with $100 and lose 10%, you have $90 left. It requires a subsequent return of about 11% to breakeven, getting you back to your original $100 stake. But if you lose 50%, going from $100 to $50, you need a subsequent return of 100% to breakeven. In plain English, the bigger the hole you get into, the harder it is to get out of. Buffett knows this well and hence the reasons for his Rule No. 1 and Rule No. 2.
The Key to Selecting a Well-Diversified Portfolio: Correlation
There are a lot of approaches to selecting a portfolio. You can take a “shotgun” approach and randomly pick a bunch of different investments. That doesn't sound too smart. A lot of people choose to equal weight their portfolios at inception. For example, this may mean if you have $10,000 to invest, you might put $1,000 each into 10 different investments. Behavioral economists actually have a name for this approach, called the 1 over N (1/N) heuristic. A heuristic is a rule of thumb that people use to solve a problem. So if you have 10 choices, you'd put 10% in each option under the 1/N heuristic. If you had 20 choices, you'd put 5% in each choice. The 1/N heuristic isn't bad, but it doesn't look beneath the surface at what drives risk, at least according to one metric that we'll discuss next.
Correlation is a term that measures how two assets move—or don't move—together. Mathematically, it's a number that ranges between positive one and negative one. If two investments have a correlation of –1, when one investment goes up, the other investment always goes down. Similarly, if one investment goes down, the other investment always goes up. In a minute, we'll give you an example with two investments that shows if they have a correlation of –1, it is possible to construct a portfolio with zero risk.
If the correlation between two investments is +1, then one investment is essentially a carbon copy of the other. When one goes up, the other always goes up, and when one goes down, the other always goes down. As you might guess, this type of investment pair provides no meaningful amount of risk reduction. If the correlation between two investments is 0, it means there is no relationship between them. When one goes up, the other may go up, down, or remain unchanged. Two investments that have a correlation of 0 provide good risk reduction properties, but not as good as if it were –1. Let's illustrate this concept with an example.
A (Theoretical) Portfolio with No Risk
To illustrate the power of two investments with negative correlation, suppose there are only two companies in the entire stock market. We like the beach, so let's assume one company sells suntan lotion and the other company sells umbrellas. We know some people purchase umbrellas to shield themselves from the sun, but let's assume most buy them to keep themselves from getting wet on a rainy day.
Suppose on sunny days the suntan lotion company is making a killing. Let's say it's up 30% due to its huge swell of profits. But on rainy days, not too many people are coming to the beach, and the firm loses 10% due to the fixed costs of running the business (e.g., rent and salaries). But on rainy days, it's the umbrella company that's making a killing. Let's say it's making 30% to keep the numbers symmetric. On sunny days, let's also assume it loses 10% due to the costs of running the business and not too many people buying umbrellas, except for the people trying to shield themselves from the sun.
Okay, we're almost ready for the punchline. Let's assume the chance of rain or shine is the same, 50%. If you put all of your money in one company, either the suntan lotion company or the umbrella company, your wealth is entirely dependent on something you have no control over—the weather. You either make 30% or lose 10%. But if you put half your money in the suntan lotion company and half your money in the umbrella company, you are guaranteed a profit on the overall portfolio, rain or shine. Instead of rolling the dice on the weather, you make money when it is sunny with the suntan lotion company, which more than offsets the loss from the umbrella company. When it rains, the profits you make on the umbrella company more than offset the losses from the suntan lotion. So there we have it. A guaranteed profit rain or shine! In this fictional example, the correlation between the suntan lotion and umbrella company is negative one.
The art of selecting an optimal portfolio is to find investments that don't move in synch with each other (low correlation in mathematical terms). In practice, many investments have a positive correlation since they are all part of the same economic boat—the world economy. But intelligent diversification can still meaningfully reduce risk. Not all companies move in lockstep fashion, especially if they are from different industries and located in different countries. Berkshire itself is the combination of many companies that are unrelated, or what economists call a conglomerate. After all, car insurance has little to do with an electric utility, railroad, furniture store, or candy shop. As we know, these are just a handful of Berkshire's many businesses.
Selecting an Optimal Diversified Portfolio: The “Business School” Approach
We'll first cover what business schools teach as the optimal way to select a portfolio, since the purpose of this book is to improve your financial literacy. We'll cover later in the chapter two approaches that Buffett favors. The “business school” approach to selecting an optimal portfolio was developed by a young graduate student named Harry Markowitz, back in the 1950s. Since recent changes to his approach have been merely incremental in nature, it still falls under the umbrella of “Modern Portfolio Theory”—more than 60 years later.
Markowitz's approach relies heavily on the concept of correlation, which we just covered, since selecting investments that have low correlation among each other results in the creation of portfolios with relatively lower amounts of risk. He also realized that people made trade-offs between things when making decisions. For example, you might look cool in an expensive Ferrari, but you probably can't afford it. When purchasing a car, you balance what you want versus what you can afford. When selecting a portfolio, you have to balance its risk with the expected return. We use the term “expected return” since your actual return can only be determined at some point in the future, after you've selected the investments.
Although the past is a very rough guide to the future, in some instances, you can't rely on it. Otherwise, investors would simply pick the stocks that went up the most in the past (e.g., Apple, Amazon.com, Microsoft, and Berkshire). Future competition, new inventions, and the missteps of companies may result in their future returns looking a lot different from their past returns. Buffett has a humorous quote on the topic, citing the Forbes 400, an annual list of the richest people in America. He said, “If history books were the key to riches, the Forbes 400 would consist of librarians.” It's a spin on the standard investments disclaimer, “Past performance is no guarantee of future results.” Let's put Buffett's quote in as a Tip to cement the idea that the future performance of an investment might look a lot different than its past performance.
Markowitz coined the term “efficient portfolio,” which maximizes the expected return of your portfolio, given the risk you are willing to take. Since risk and return are two sides of the same coin, an efficient portfolio is also one that minimizes risk, given an expected return that you want to receive. If you map out all of the possible efficient portfolios for a given set of investments, it results in a curve (technically a parabola) called an efficient frontier. A picture of an efficient frontier is shown in Figure 8.1.
You can view the efficient frontier as the menu of good diversified portfolios. Investments that fall below the efficient frontier are inefficient and are dominated by the good ones. The inefficient ones have less return for the same amount of risk or more risk for the same amount of return. There are a lot of analogies that we can use to explain this concept. Most people can relate to food. The efficient portfolios are similar to a menu of good food items at a Chinese buffet. (We could use any cuisine, but buffet sounds similar to Buffett, and we don't want you to spell Buffett's name incorrectly, so we expect this note to stick in your mind). The bad (or inefficient) food at the Chinese buffet either tastes poorly, isn't fresh, or isn't worthy of making it on the menu. So now we can get to the question next addressed by Markowitz. That is, “What is the optimal diversified portfolio for me?”
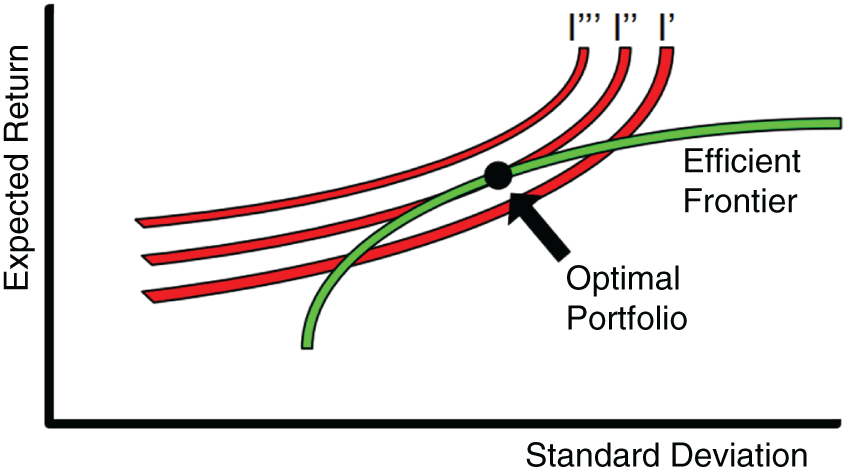
Figure 8.1 Selecting an Optimal Portfolio from the Efficient Frontier
Sticking with our Chinese buffet analogy, even though you might like Chinese food, you probably won't eat everything on the menu. Similarly, Markowitz used a way to measure your willingness to trade off things, specifically, risk and return. The formal term for measuring this trade-off is with something economists call an indifference curve. In a portfolio selection context, it measures your willingness to trade off between two things, risk and return. You might be willing to take on a little more risk if you expected to get a little bit more return. Similarly, you might be willing to take a little bit lesser return if your portfolio had less risk. The optimal diversified portfolio matches the efficient frontier (the menu of good investment combinations) with your indifference curve (the items at the Chinese buffet that you like), which measures your willingness to trade off risk and return. The optimal portfolio is shown in Figure 8.1 as the point of tangency between the two curves, the efficient frontier and your unique indifference curve.
If you find this approach compelling, there is some free software online that can help you select an optimal portfolio. One good website that helps with the portfolio selection problem using the Markowitz approach is:
https://www.portfoliovisualizer.com/optimize-portfolio
.
Most investment firms also have software that can perform something similar for their clients.
Buffett's First Approach to Portfolio Selection: Index Funds
Buffett has two approaches to picking a portfolio. For most people, he suggests an index fund, such as the S&P 500, which consists of 500 large American stocks spread across a range of industries. We've mentioned index funds before and listed their benefits as a prior Tip. It's basically a “set it and forget it” buy-and-hold strategy of a basket of investments that charges minimal fees. We'll focus on stock indexes here since it may be the main holding for a young person, but there are index funds on bonds, real estate, and other assets. If a stock index portfolio has too much risk for you, mixing it with other index funds should lower the overall risk of the portfolio over time.
Besides the low expenses and minimal effort involved, stock index funds have the advantage of owning some of the largest and most successful firms in America, such as Apple, Alphabet (Google), Exxon Mobil, Starbucks, Microsoft, Berkshire Hathaway, Johnson & Johnson, and many others. These large firms are less likely to go bankrupt and many also pay a dividend. The S&P 500 is a value- or market capitalization–weighted index, which means the larger, more valuable stocks, such as Microsoft, have a greater effect on the index's returns than the smaller ones.
Since no one can time when to get in and out of the market with any high degree of certainty, Buffett further advises investors to buy index funds periodically over time. This approach is known as dollar cost averaging. It guarantees that you won't buy near the market high, or the market low. It also relates to how most people typically invest, taking money out of their paychecks and putting it into their retirement plans every couple of weeks or month.
Buffett's Second Approach to Portfolio Selection: Expert Mode
Buffett's second recommended approach is for someone who is a “know something” (as opposed to know nothing) investor. Knowing something is a minimal hurdle, so we'll refer to someone picking their own investments as a person operating in “expert mode,” at least within their circle of competence. By that expression, we mean someone willing to put the time and effort into understanding what a firm does and what it is worth, before investing. This approach also requires following the firm closely to make sure the reasons why you purchased the stock are still valid. For example, in Chapter 6 we talked about companies having a moat that helps them fend off competition. If the moat of a firm is eroding, it might be time to sell. Buffett typically puts a large percentage of his assets in a relatively small group of stocks. Folks on Wall Street often call this a high-conviction or best-ideas approach, which involves putting the bulk of your assets in a relatively small number of investments. It results in highly concentrated portfolios as opposed to a broadly diversified index fund.
For example, Buffett once put roughly 40% of his investors' assets in a single stock, American Express, when the firm ran into problems back in the 1960s. Forty percent is a huge amount to put in any investment, so hopefully you can see how we view Buffett's high-conviction approach to creating a portfolio as falling under the “expert mode.” A few bad decisions in a highly concentrated portfolio could put yourself in a big hole that is hard to recover from.
Buffett has always operated this way and not just during his young, gunslinger days. Large investment managers (i.e., those managing more than $100 million) have to file quarterly reports with the SEC, called Form 13-F, that detail some of their holdings. There are various websites that track this data. Our favorite site that tracks 13-F data is WhaleWisdom.com. A whale in Wall Street jargon refers to a large investor. For example, at the end of 2019 Berkshire Hathaway had more than 67% of its investments in only five stocks: Apple (29.7%), Bank of America (13.5%), Coca-Cola (9.2%), American Express (7.8%), and Wells Fargo (7.2%). These firms are generally regarded as high-quality companies that pay a dividend and have a long operating history. These attributes are some of the ways Buffett aims to control risk, as well as his detailed understanding of each company that he invests in. Notice that in his top holdings there are no recent IPOs, companies that are losing money, that or don't have a long-term history. Buffett thinks six stocks are enough for someone operating a portfolio in “expert” mode.
In a talk Buffett gave to students at the University of Florida, he said, “If you can identify six wonderful businesses, that is all the diversification you need. And you will make a lot of money. And I can guarantee that going into a seventh one instead of putting more money into your first one is gotta be a terrible mistake. Very few people have gotten rich on their seventh best idea. But a lot of people have gotten rich with their best idea. So, I would say for anyone working with normal capital who really knows the businesses they have gone into, six is plenty.” Let's turn the essence of that quote into a Tip.
In his 1993 Letter to Berkshire Shareholders, Buffett expanded on his thoughts on diversification. He said, “We believe that a policy of portfolio concentration may well decrease risk if it raises, as it should, both the intensity with which an investor thinks about a business and the comfort level he must feel with its economic characteristics before buying into it.” Let's also summarize that quote with a Tip.
A Compromise Solution to Portfolio Selection
If you don't have the interest, time, or expertise to follow the Buffett “expert” mode approach to selecting a portfolio, a compromise might be to construct your own diversified “mini index.” One approach that we like is to select the biggest firm, by market capitalization, in each industry. We call it the “terminator portfolio” in homage to a famous cyborg character Arnold Schwarzenegger played a couple of decades ago. These firms, like the Schwarzenegger character, tend to dominate the competition. For example, the portfolio might consist of the largest oil firm in the US, ExxonMobil, the largest consumer firm, Apple, the largest restaurant, McDonald's, the largest bank, J.P. Morgan, and so forth. This “mini index” portfolio would likely return something similar to the S&P 500 since it would account for roughly 80% of the market capitalization weight of the S&P 500. You might also learn something by watching these leading firms closely (i.e., you automatically get an annual report of each stock owned) and may eventually transition into an “expert mode.”
One way to get practice with investing, even if you have no money, is to use a free investment simulator. A simulator allows you to manage a “paper portfolio” of any amount (e.g., $1 million in fictional money) and track the results. There are several investment simulators out there. Our favorite free one can be found at Investopedia.com. Click for the “Simulator” link and proceed from there. You could even set up multiple paper portfolios corresponding to different investment strategies until you find your favorite approach.
How Many Stocks Make a Diversified Portfolio?
Buffett thinks diversification “makes little sense if you know what you are doing.” However, most people aren't comfortable with the notion of a highly concentrated portfolio. This raises the question of “What is adequate diversification?” The answer depends on what is in your portfolio.
For example, a single S&P 500 index fund may be adequate diversification for someone's stock holdings since this single investment holds the equivalent of 500 stocks. So let's tackle the question of what might be adequate diversification for someone picking their own individual stocks and are not quite ready to go into the Buffett expert mode of a highly concentrated portfolio. Fortunately, there have been many studies on the topic. In Chapter 2 we mentioned that one way of measuring risk is by looking at the standard deviation of an asset's returns.
If you have a portfolio with only one stock, decades of academic research find it has a ton of risk, or a standard deviation of roughly 30% in statistical terms. But the good news is that risk is reduced rapidly as you keep adding securities to your portfolio. By the time you have 10 stocks in the portfolio, studies find the risk is cut by about 40%. Once you get to about 30 securities your risk is cut by almost half. Once you get past 100 stocks, there is not much more risk reduction to be had. Plus 100 stocks is a lot to follow. So to answer the question we posed at the top of this section, to have a well-diversified portfolio, 30 is a good round number of how many stocks you need. If you're more adventurous, even 15 to 20 might be enough.
However, we emphasize that the 30 stocks should be spread across a number of different industries (at least 15). Owning 30 tech stocks (or others in the same industry) is not likely to provide much additional risk reduction since the correlation among the securities will probably be high.
The “Business School” Approach to Risk
Buffett takes issue with how business schools usually teach the subject of risk. To better understand Buffett's critique and to enhance your financial literacy, we'll cover the essence of the major theory on risk and return taught in most business schools. It's called the Capital Asset Pricing Model (CAPM), and it's an extension of Markowitz's work. To get there, let's start with a picture that we've labeled as Figure 8.2.
The more stocks you add to the portfolio, the more risk is reduced. Here we are still using standard deviation of the stock's returns (i.e., its volatility) as the measure of risk. As you keep adding more and more stocks to the portfolio, the diversifiable—or company-specific—risk is reduced. Notice that even if you own all the stocks in the market (e.g., an index fund with thousands of stocks), you still can't get rid of the market risk. One easy way to see this is that the market goes up or down on a daily basis. If market risk could be completely diversified away, the market would never go down. But we know that it does, and sometimes by huge amounts.
Academics call market risk by the Greek alphabet letter beta. It's also known as systematic risk, since it's tied to the economic system. Here's the insight that academics believe is important. The only risk worth paying for (i.e., that should give you a meaningful return) is the risk that can't be diversified away, beta. According to the theory, company-specific risk should then be irrelevant when buying a stock, since if you diversify enough, it will disappear.

Figure 8.2 Graph of the “Business School” Approach to Risk
The CAPM says that the expected return on any stock is equal to the risk-free rate of interest plus the product of stock's beta and another item we'll cover in a second. In practice, the risk-free rate of interest is a government bond with a maturity equal to your time horizon (e.g., one year). Any investment worth its salt should beat the risk-free rate of interest, on average; otherwise, no one would invest in it. We've just covered beta, a measure of market risk. Not all stocks have the same beta. The beta for the market as a whole is 1. Some stocks have a beta less than 1. These tend to be large, well-established firms, or companies that operate in less volatile industries, including food, beverages, utilities, and large pharmaceutical firms. But some firms have a beta greater than 1. These often include small firms and firms in more volatile industries, such as technology, biotechnology, banks, autos, and some retail stocks.
Getting back to the CAPM, we have the risk-free rate of interest, beta, and one more factor. This last factor is tied to market psychology. It relates to how much risk investors are willing to take in the market as a whole. It's called the market risk premium and is the difference between the expected return on the stock market and the risk-free rate of interest. To make this concept less abstract, the US stock market historically returns about 10% per year, and the risk-free rate of interest, as represented by a Treasury bill, historically returns about 3% a year, even though today it's close to 0%. This analysis would give a historical market risk premium of about 7% a year. But market psychology is fickle, as we discussed with our Mr. Market and pendulum analogies in our chapter on stocks. Sometimes people are fearful, and the market risk premium might spike to around 10% or more. Other times people are greedy or complacent and the number shrinks to 2% or 3%. In this case, people don't require much more extra return to invest in stocks. The market risk premium number is the same for all stocks in the market and is not tied to its beta.
Putting it all together, the CAPM says the expected return for any stock is equal to the risk-free rate of interest plus the stock's beta, times the market risk premium. It results in a straight-line relationship between expected risk and return as shown in Figure 8.3. In case you're mathematically inclined, we put the full CAPM equation in an endnote.
Summing this section up, in business school they teach that beta (market risk) is the main way of measuring risk. Sometimes they combine it with things that we discussed in Chapter 5, such as size (i.e., large cap vs. small cap), style (i.e., growth vs. value), as well as the recent trend in price, known as momentum.

Figure 8.3 Graph of the Capital Asset Pricing Model
Buffett's Critique of the Business School Approach to Risk
There's a good reason why we discussed beta and the CAPM model, even though you may have found it about as dull as dirt. Buffett has an issue with how they define and teach risk in business schools. We touched upon some of these issues but will now add more detail to his critique. And because he's Buffett, we think he's right. First, back in Chapter 2 we noted Buffett's definition of risk—the possibility of loss or injury. We also noted that he said, over the long run, bonds and cash are riskier than stocks since they often fail to keep up with inflation, especially on an after-tax basis.
But he has more to say on the topic of risk, and we needed to cover specific measures of risk such as standard deviation and beta in more depth in order to address his critique further. Having a concentrated portfolio, and its usual corresponding high levels of standard deviation, doesn't bother Buffett since he thinks standard deviation is a flawed measure of risk. He doesn't give it a second thought.
He thinks beta is flawed too. He couldn't care less about it either. In his 1993 Letter to Berkshire Shareholders, he wrote, “Employing data bases and statistical skills, these academics compute with precision the ‘beta’ of a stock—its relative volatility in the past—and then build arcane investment and capital-allocation theories around this calculation. In their hunger for a single statistic to measure risk, however, they forget a fundamental principle: It is better to be approximately right than precisely wrong.”
This last sentence is a similar comment to our prior tip on “beware of geeks bearing formulas,” but since it's a direct attack on what is taught in business schools, we'll put the essence of his critique as a separate Tip.
Buffett's Approach to Risk
Buffett's approach to risk is to focus on what the company does and how it may be affected by its competition, or what we called the strength of its moat. He thinks it's crazy to say a firm with the same beta as Coca-Cola or Gillette (now owned by Procter and Gamble, P&G) has the same risk as some “fly by night firm” that is new or has shaky financials. This firm, let's called it Beta Inc., likely doesn't have the history and moat of Coke or P&G and therefore shouldn't have the same risk. In his 1993 Letter to Berkshire Shareholders he wrote:
The competitive strengths of a Coke or Gillette are obvious to even the casual observer of business. Yet the beta of their stocks is similar to that of a great many run-of-the-mill companies who possess little or no competitive advantage. Should we conclude from this similarity that the competitive strength of Coke and Gillette gains them nothing when business risk is being measured? Or should we conclude that the risk in owning a piece of a company—its stock—is somehow divorced from the long-term risk inherent in its business operations? We believe neither conclusion makes sense and that equating beta with investment risk also makes no sense.
He goes on to say, “In assessing risk, a beta purist will disdain examining what a company produces, what its competitors are doing, or how much borrowed money the business employs. He may even prefer not to know the company's name. What he treasures is the price history of its stock. In contrast, we'll happily forgo knowing the price history and instead will seek whatever information will further our understanding of the company's business.”
Let's summarize these views on risk with another Tip.
When you want to buy something and it drops in price, you probably think you're getting a good deal. The risk that you overpaid for the product or service you purchased is reduced. Buffett says the same concept should apply to investing. In his 1993 Letter to Berkshire Shareholders, Buffett said, “For example, under beta-based theory, a stock that has dropped very sharply compared to the market—as had The Washington Post when we bought it in 1973—becomes ‘riskier’ at the lower price than it was at the higher price. Would that description have then made any sense to someone who was offered the entire company at a vastly reduced price? In fact, the true investor welcomes volatility.”
That's great advice from the Oracle of Omaha, even though it's hard for many people to follow. Why? When a stock you own falls in price, it decreases your net worth, leaving you poorer. This causes many investors huge anxiety and has them reaching for some antacids. Let's put the last line in Buffett's quote in as a Tip.
Buffett on Gold
Gold is often considered a safe-haven asset. That is, it typically goes up when stocks fall sharply. It often has a negative correlation to stocks, so academics usually like it for its diversification properties. So what does Buffett have to say about gold? Like with Bitcoin, Buffett is not a fan. Buffett doesn't believe gold is a productive asset. By that, we mean the following: A farm produces food. Real estate produces rent or serves as a home. Bonds pay interest, in addition to the principal. Stocks represent ownership in a business and often pay dividends. But gold? It looks nice and can be used for jewelry, but Buffett doesn't think it has much value. In his 2011 Letter to shareholders he wrote:
Today the world's gold stock is about 170,000 metric tons. If all of this gold were melded together, it would form a cube of about 68 feet per side. (Picture it fitting comfortably within a baseball infield.) At $1,750 per ounce—gold's price as I write this—its value would be $9.6 trillion. Call this cube pile A.
Let's now create a pile B costing an equal amount. For that, we could buy all US cropland (400 million acres with output of about $200 billion annually), plus 16 Exxon Mobils (the world's most profitable company, one earning more than $40 billion annually). After these purchases, we would have about $1 trillion left over for walking-around money (no sense feeling strapped after this buying binge). Can you imagine an investor with $9.6 trillion selecting pile A over pile B?
A century from now the 400 million acres of farmland will have produced staggering amounts of corn, wheat, cotton, and other crops—and will continue to produce that valuable bounty, whatever the currency may be. Exxon Mobil will probably have delivered trillions of dollars in dividends to its owners and will also hold assets worth many more trillions (and, remember, you get 16 Exxons). The 170,000 tons of gold will be unchanged in size and still incapable of producing anything. You can fondle the cube, but it will not respond.
It's a long quote, but one worth remembering the next time some doomsayer tells you to put a big chunk of your money in gold. Let's summarize his views on gold with a Tip.
Summarizing Buffett's Views on Risk
Risk isn't an easy topic to grasp on first sitting, but it's one of the most important subjects for your financial and personal well-being. To summarize some of Buffett's views, risk is having an investment that can't outperform inflation on an after-tax basis. It's investing in businesses that you don't understand, that have poor management, have too much debt, have no competitive advantage, or are overvalued.
He laid it out more formally in his 1993 Letter to Berkshire Shareholders. It's sort of a lengthy quote, but hang on a bit longer since you've finally reached the end of this chapter. Plus, it's not an equation like you might find in a textbook on investments. According to Buffett, risk is determined by:
- The certainty with which the long-term economic characteristics of the business can be evaluated;
- The certainty with which management can be evaluated, both as to its ability to realize the full potential of the business and to wisely employ its cash flows;
- The certainty with which management can be counted on to channel the rewards from the business to the shareholders rather than to itself;
- The purchase price of the business;
- The levels of taxation and inflation that will be experienced and that will determine the degree by which an investor's purchasing-power return is reduced from his gross return.
Endnote on CAPM
The main CAPM equation (often called the Security Market Line) is listed below, using IBM as an example.
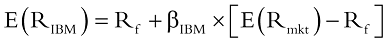
It says the expected return on IBM is equal to the risk-free rate of interest plus the product of the beta for IBM and the market risk premium. The risk-free rate of interest and the market risk premium, theoretically, are the same for all firms, so differences in expected return for different assets essentially boil down to differences in beta, according to CAPM.
References
- Bodie, Zvi, Alex Kane, and Alan J. Marcus. Investments, 10th edition. New York: McGraw-Hill Education, 2013.
- Buffett, Warren. “Letter to Shareholders of Berkshire Hathaway Inc.” Berkshire Hathaway, Inc., 1993. https://www.berkshirehathaway.com/letters/1993.html.
- Buffett, Warren. “Letter to Shareholders of Berkshire Hathaway Inc.” Berkshire Hathaway, Inc., 2011. https://www.berkshirehathaway.com/letters/2011.html.
- Buffett, Warren. “Warren Buffett: Why Stocks Beat Gold and Bonds.” Fortune, February 9, 2012. https://fortune.com/2012/02/09/warren-buffett-why-stocks-beat-gold-and-bonds/.
- Investment Master Class. “Diversification or Concentration? Quotes from Some of the Best Investors.” ValueWalk, January 15, 2017. https://www.valuewalk.com/2017/01/diversification-concentration-quotes-best-investors/.
- Kroll, Luisa, and Kerry A Dolan, eds. “The Forbes 400 2019.” Forbes, October 2, 2019. https://www.forbes.com/forbes-400/.
- LeylandPAM . “Warren Buffett speaks with Florida University.” YouTube Video, 1:27:35, July 2, 2013, https://www.youtube.com/watch?v=2MHIcabnjrA.
- Loiacono, Stephanie. “Rules That Warren Buffett Lives By.” Yahoo! Finance, February 23, 2010. https://web.archive.org/web/20111229015815/http://finance.yahoo.com/news/pf_article_108903.html.
- Markowitz, Harry. “Portfolio Selection.” Journal of Finance 7, no. 1 (1952): 77–91. https://doi.org/10.2307/2975974.
- Markowitz, Harry. Portfolio Selection: Efficient Diversification of Investments. New York: Wiley, 1970.
- Saft, James. “Buffett Champions Conglomerates, Don't Believe Him,” March 4, 2015. http://blogs.reuters.com/james-saft/2015/03/04/buffett-champions-conglomerates-dont-believe-him/.
- Udland, Myles. “Warren Buffett Defends Berkshire's Conglomerate Structure—and Fires a Huge Shot at Private Equity.” Business Insider, February 28, 2015. http://www.businessinsider.com/warren-buffett-on-conglomerates-and-private-equity-2015-2.
- Whitby, Jason. “The Illusion of Diversification: The Myth of the 30 Stock Portfolio.” Investopedia, June 25, 2019. http://www.investopedia.com/articles/stocks/11/illusion-of-diversification.asp.