In previous lessons, we learned how to conduct hypothesis tests that examined the relationship between two variables. Most of these tests simply evaluated the relationship of the means of two variables. However, sometimes we also want to test the variance, or the degree to which observations are spread out within a distribution. In the figure below, we see three samples with identical means (the samples in red, green, and blue) but with very difference variances:

So why would we want to conduct a hypothesis test on variance? Let’s consider an example. Suppose a teacher wants to examine the effectiveness of two reading programs. She randomly assigns her students into two groups, uses a different reading program with each group, and gives her students an achievement test. In deciding which reading program is more effective, it would be helpful to not only look at the mean scores of each of the groups, but also the “spreading out” of the achievement scores. To test hypotheses about variance, we use a statistical tool called the ![]() -distribution.
-distribution.
In this lesson, we will examine the difference between the ![]() -distribution and Student’s
-distribution and Student’s ![]() -distribution, calculate a test statistic with the
-distribution, calculate a test statistic with the ![]() -distribution, and test hypotheses about multiple population variances. In addition, we will look a bit more closely at the limitations of this test.
-distribution, and test hypotheses about multiple population variances. In addition, we will look a bit more closely at the limitations of this test.
The ![]() -distribution is actually a family of distributions. The specific
-distribution is actually a family of distributions. The specific ![]() -distribution for testing two population variances,
-distribution for testing two population variances, ![]() and
and ![]() , is based on two values for degrees of freedom (one for each of the populations). Unlike the normal distribution and the
, is based on two values for degrees of freedom (one for each of the populations). Unlike the normal distribution and the ![]() -distribution,
-distribution, ![]() -distributions are not symmetrical and span only non-negative numbers. (Normal distributions and
-distributions are not symmetrical and span only non-negative numbers. (Normal distributions and ![]() -distributions are symmetric and have both positive and negative values.) In addition, the shapes of
-distributions are symmetric and have both positive and negative values.) In addition, the shapes of ![]() -distributions vary drastically, especially when the value for degrees of freedom is small. These characteristics make determining the critical values for
-distributions vary drastically, especially when the value for degrees of freedom is small. These characteristics make determining the critical values for ![]() -distributions more complicated than for normal distributions and Student’s
-distributions more complicated than for normal distributions and Student’s ![]() -distributions.
-distributions. ![]() -distributions for various degrees of freedom are shown below:
-distributions for various degrees of freedom are shown below:

We use the ![]() -ratio test statistic when testing the hypothesis that there is no difference between population variances. When calculating this ratio, we really just need the variance from each of the samples. It is recommended that the larger sample variance be placed in the numerator of the
-ratio test statistic when testing the hypothesis that there is no difference between population variances. When calculating this ratio, we really just need the variance from each of the samples. It is recommended that the larger sample variance be placed in the numerator of the ![]() -ratio and the smaller sample variance in the denominator. By doing this, the ratio will always be greater than 1.00 and will simplify the hypothesis test.
-ratio and the smaller sample variance in the denominator. By doing this, the ratio will always be greater than 1.00 and will simplify the hypothesis test.
Example: Suppose a teacher administered two different reading programs to two groups of students and collected the following achievement score data:

What is the ![]() -ratio for these data?
-ratio for these data?
![]()
When we test the hypothesis that two variances of populations from which random samples were selected are equal, ![]() (or in other words, that the ratio of the variances
(or in other words, that the ratio of the variances ![]() ), we call this test the
), we call this test the ![]() -Max test. Since we have a null hypothesis of
-Max test. Since we have a null hypothesis of ![]() , our alternative hypothesis would be
, our alternative hypothesis would be ![]() .
.
Establishing the critical values in an ![]() -test is a bit more complicated than when doing so in other hypothesis tests. Most tables contain multiple
-test is a bit more complicated than when doing so in other hypothesis tests. Most tables contain multiple ![]() -distributions, one for each of the following: 1 percent, 5 percent, 10 percent, and 25 percent of the area in the right-hand tail. (Please see the supplemental link for an example of this type of table.) We also need to use the degrees of freedom from each of the samples to determine the critical values.
-distributions, one for each of the following: 1 percent, 5 percent, 10 percent, and 25 percent of the area in the right-hand tail. (Please see the supplemental link for an example of this type of table.) We also need to use the degrees of freedom from each of the samples to determine the critical values.
On the Web
http://www.statsoft.com/textbook/sttable.html#f01 ![]() -distribution tables.
-distribution tables.
Example: Suppose we are trying to determine the critical values for the scenario in the preceding section, and we set the level of significance to 0.02. Because we have a two-tailed test, we assign 0.01 to the area to the right of the positive critical value. Using the ![]() -table for
-table for ![]() , we find the critical value at 2.203, since the numerator has 30 degrees of freedom and the denominator has 40 degrees of freedom.
, we find the critical value at 2.203, since the numerator has 30 degrees of freedom and the denominator has 40 degrees of freedom.
Once we find our critical values and calculate our test statistic, we perform the hypothesis test the same way we do with the hypothesis tests using the normal distribution and Student’s ![]() -distribution.
-distribution.
Example: Using our example from the preceding section, suppose a teacher administered two different reading programs to two different groups of students and was interested if one program produced a greater variance in scores. Perform a hypothesis test to answer her question.
For the example, we calculated an ![]() -ratio of 2.909 and found a critical value of 2.203. Since the observed test statistic exceeds the critical value, we reject the null hypothesis. Therefore, we can conclude that the observed ratio of the variances from the independent samples would have occurred by chance if the population variances were equal less than 2% of the time. We can conclude that the variance of the student achievement scores for the second sample is less than the variance of the scores for the first sample. We can also see that the achievement test means are practically equal, so the difference in the variances of the student achievement scores may help the teacher in her selection of a program.
-ratio of 2.909 and found a critical value of 2.203. Since the observed test statistic exceeds the critical value, we reject the null hypothesis. Therefore, we can conclude that the observed ratio of the variances from the independent samples would have occurred by chance if the population variances were equal less than 2% of the time. We can conclude that the variance of the student achievement scores for the second sample is less than the variance of the scores for the first sample. We can also see that the achievement test means are practically equal, so the difference in the variances of the student achievement scores may help the teacher in her selection of a program.
The test of the null hypothesis, ![]() , using the
, using the ![]() -distribution is only appropriate when it can safely be assumed that the population is normally distributed. If we are testing the equality of standard deviations between two samples, it is important to remember that the
-distribution is only appropriate when it can safely be assumed that the population is normally distributed. If we are testing the equality of standard deviations between two samples, it is important to remember that the ![]() -test is extremely sensitive. Therefore, if the data displays even small departures from the normal distribution, including non-linearity or outliers, the test is unreliable and should not be used. In the next lesson, we will introduce several tests that we can use when the data are not normally distributed.
-test is extremely sensitive. Therefore, if the data displays even small departures from the normal distribution, including non-linearity or outliers, the test is unreliable and should not be used. In the next lesson, we will introduce several tests that we can use when the data are not normally distributed.
We use the ![]() -Max test and the
-Max test and the ![]() -distribution when testing if two variances from independent samples are equal.
-distribution when testing if two variances from independent samples are equal.
The ![]() -distribution differs from the normal distribution and Student’s
-distribution differs from the normal distribution and Student’s ![]() -distribution. Unlike the normal distribution and the
-distribution. Unlike the normal distribution and the ![]() -distribution,
-distribution, ![]() -distributions are not symmetrical and go from 0 to
-distributions are not symmetrical and go from 0 to ![]() , not from
, not from ![]() to
to ![]() as the others do.
as the others do.
When testing the variances from independent samples, we calculate the ![]() -ratio test statistic, which is the ratio of the variances of the independent samples.
-ratio test statistic, which is the ratio of the variances of the independent samples.
When we reject the null hypothesis, ![]() , we conclude that the variances of the two populations are not equal.
, we conclude that the variances of the two populations are not equal.
The test of the null hypothesis, ![]() , using the
, using the ![]() -distribution is only appropriate when it can be safely assumed that the population is normally distributed.
-distribution is only appropriate when it can be safely assumed that the population is normally distributed.

(a) What are the null and alternative hypotheses for this scenario?
(b) What is the critical value with ![]() ?
?
(c) Calculate the ![]() -ratio.
-ratio.
(d) Would you reject or fail to reject the null hypothesis? Explain your reasoning.
(e) Interpret the results and determine what the guidance counselor can conclude from this hypothesis test.
Previously, we have discussed analyses that allow us to test if the means and variances of two populations are equal. Suppose a teacher is testing multiple reading programs to determine the impact on student achievement. There are five different reading programs, and her 31 students are randomly assigned to one of the five programs. The mean achievement scores and variances for the groups are recorded, along with the means and the variances for all the subjects combined.
We could conduct a series of ![]() -tests to determine if all of the sample means came from the same population. However, this would be tedious and has a major flaw, which we will discuss shortly. Instead, we use something called the Analysis of Variance (ANOVA), which allows us to test the hypothesis that multiple population means and variances of scores are equal. Theoretically, we could test hundreds of population means using this procedure.
-tests to determine if all of the sample means came from the same population. However, this would be tedious and has a major flaw, which we will discuss shortly. Instead, we use something called the Analysis of Variance (ANOVA), which allows us to test the hypothesis that multiple population means and variances of scores are equal. Theoretically, we could test hundreds of population means using this procedure.
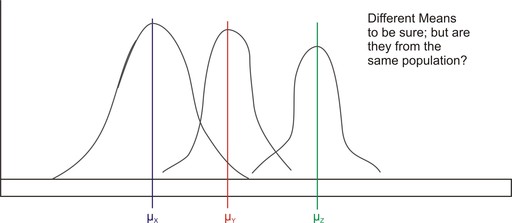
As mentioned, to test whether pairs of sample means differ by more than we would expect due to chance, we could conduct a series of separate ![]() -tests in order to compare all possible pairs of means. This would be tedious, but we could use a computer or a TI-83/84 calculator to compute these quickly and easily. However, there is a major flaw with this reasoning.
-tests in order to compare all possible pairs of means. This would be tedious, but we could use a computer or a TI-83/84 calculator to compute these quickly and easily. However, there is a major flaw with this reasoning.
When more than one ![]() -test is run, each at its own level of significance, the probability of making one or more type I errors multiplies exponentially. Recall that a type I error occurs when we reject the null hypothesis when we should not. The level of significance,
-test is run, each at its own level of significance, the probability of making one or more type I errors multiplies exponentially. Recall that a type I error occurs when we reject the null hypothesis when we should not. The level of significance, ![]() , is the probability of a type I error in a single test. When testing more than one pair of samples, the probability of making at least one type I error is
, is the probability of a type I error in a single test. When testing more than one pair of samples, the probability of making at least one type I error is ![]() , where
, where ![]() is the level of significance for each
is the level of significance for each ![]() -test and
-test and ![]() is the number of independent
is the number of independent ![]() -tests. Using the example from the introduction, if our teacher conducted separate
-tests. Using the example from the introduction, if our teacher conducted separate ![]() -tests to examine the means of the populations, she would have to conduct 10 separate
-tests to examine the means of the populations, she would have to conduct 10 separate ![]() -tests. If she performed these tests with
-tests. If she performed these tests with ![]() , the probability of committing a type I error is not 0.05 as one would initially expect. Instead, it would be 0.40, which is extremely high!
, the probability of committing a type I error is not 0.05 as one would initially expect. Instead, it would be 0.40, which is extremely high!
With the ANOVA method, we are actually analyzing the total variation of the scores, including the variation of the scores within the groups and the variation between the group means. Since we are interested in two different types of variation, we first calculate each type of variation independently and then calculate the ratio between the two. We use the ![]() -distribution as our sampling distribution and set our critical values and test our hypothesis accordingly.
-distribution as our sampling distribution and set our critical values and test our hypothesis accordingly.
When using the ANOVA method, we are testing the null hypothesis that the means and the variances of our samples are equal. When we conduct a hypothesis test, we are testing the probability of obtaining an extreme ![]() -statistic by chance. If we reject the null hypothesis that the means and variances of the samples are equal, and then we are saying that the difference that we see could not have happened just by chance.
-statistic by chance. If we reject the null hypothesis that the means and variances of the samples are equal, and then we are saying that the difference that we see could not have happened just by chance.
To test a hypothesis using the ANOVA method, there are several steps that we need to take. These include:
1. Calculating the mean squares between groups, ![]() . The
. The ![]() is the difference between the means of the various samples. If we hypothesize that the group means are equal, then they must also equal the population mean. Under our null hypothesis, we state that the means of the different samples are all equal and come from the same population, but we understand that there may be fluctuations due to sampling error. When we calculate the
is the difference between the means of the various samples. If we hypothesize that the group means are equal, then they must also equal the population mean. Under our null hypothesis, we state that the means of the different samples are all equal and come from the same population, but we understand that there may be fluctuations due to sampling error. When we calculate the ![]() , we must first determine the
, we must first determine the ![]() , which is the sum of the differences between the individual scores and the mean in each group. To calculate this sum, we use the following formula:
, which is the sum of the differences between the individual scores and the mean in each group. To calculate this sum, we use the following formula:
![]()
where:
![]() is the group number.
is the group number.
![]() is the sample size of group
is the sample size of group ![]() .
.
![]() is the mean of group
is the mean of group ![]() .
.
![]() is the overall mean of all the observations.
is the overall mean of all the observations.
![]() is the total number of groups.
is the total number of groups.
When simplified, the formula becomes:
![]()
where:
![]() is the sum of the observations in group
is the sum of the observations in group ![]() .
.
![]() is the sum of all the observations.
is the sum of all the observations.
![]() is the total number of observations.
is the total number of observations.
Once we calculate this value, we divide by the number of degrees of freedom, ![]() , to arrive at the
, to arrive at the ![]() . That is,
. That is, ![]()
2. Calculating the mean squares within groups, ![]() . The mean squares within groups calculation is also called the pooled estimate of the population variance. Remember that when we square the standard deviation of a sample, we are estimating population variance. Therefore, to calculate this figure, we sum the squared deviations within each group and then divide by the sum of the degrees of freedom for each group.
. The mean squares within groups calculation is also called the pooled estimate of the population variance. Remember that when we square the standard deviation of a sample, we are estimating population variance. Therefore, to calculate this figure, we sum the squared deviations within each group and then divide by the sum of the degrees of freedom for each group.
To calculate the ![]() , we first find the
, we first find the ![]() , which is calculated using the following formula:
, which is calculated using the following formula:
![]()
Simplified, this formula becomes:
![]()
where:
![]() is the sum of the observations in group
is the sum of the observations in group ![]() .
.
Essentially, this formula sums the squares of each observation and then subtracts the total of the observations squared divided by the number of observations. Finally, we divide this value by the total number of degrees of freedom in the scenario, ![]() .
.
![]()
3. Calculating the test statistic. The formula for the test statistic is as follows:
![]()
4. Finding the critical value of the ![]() -distribution. As mentioned above,
-distribution. As mentioned above, ![]() degrees of freedom are associated with
degrees of freedom are associated with ![]() , and
, and ![]() degrees of freedom are associated with
degrees of freedom are associated with ![]() . In a table, the degrees of freedom for
. In a table, the degrees of freedom for ![]() are read across the columns, and the degrees of freedom for
are read across the columns, and the degrees of freedom for ![]() are read across the rows.
are read across the rows.
5. Interpreting the results of the hypothesis test. In ANOVA, the last step is to decide whether to reject the null hypothesis and then provide clarification about what that decision means.
The primary advantage of using the ANOVA method is that it takes all types of variations into account so that we have an accurate analysis. In addition, we can use technological tools, including computer programs, such as SAS, SPSS, and Microsoft Excel, as well as the TI-83/84 graphing calculator, to easily perform the calculations and test our hypothesis. We use these technological tools quite often when using the ANOVA method.
Example: Let’s go back to the example in the introduction with the teacher who is testing multiple reading programs to determine the impact on student achievement. There are five different reading programs, and her 31 students are randomly assigned to one of the five programs. She collects the following data:
Method
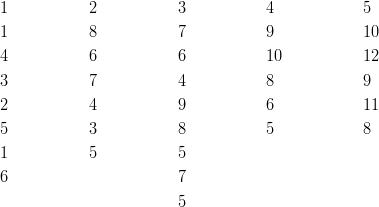
Compare the means of these different groups by calculating the mean squares between groups, and use the standard deviations from our samples to calculate the mean squares within groups and the pooled estimate of the population variance.
To solve for ![]() , it is necessary to calculate several summary statistics from the data above:
, it is necessary to calculate several summary statistics from the data above:
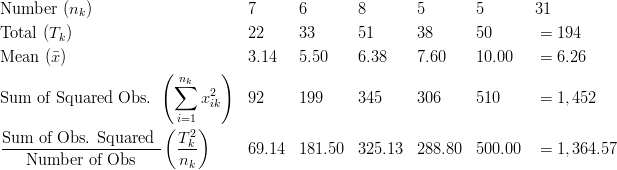
Using this information, we find that the sum of squares between groups is equal to the following:
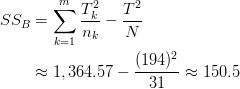
Since there are four degrees of freedom for this calculation (the number of groups minus one), the mean squares between groups is as shown below:
![]()
Next, we calculate the mean squares within groups, ![]() , which is also known as the pooled estimate of the population variance,
, which is also known as the pooled estimate of the population variance, ![]() .
.
To calculate the mean squares within groups, we first use the following formula to calculate ![]() :
:
![]()
Using our summary statistics from above, we can calculate ![]() as shown below:
as shown below:
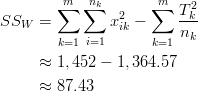
This means that we have the following for ![]() :
:
![]()
Therefore, our ![]() -ratio is as shown below:
-ratio is as shown below:
![]()
We would then analyze this test statistic against our critical value. Using the ![]() -distribution table and
-distribution table and ![]() , we find our critical value equal to 4.140. Since our test statistic of 11.19 exceeds our critical value of 4.140, we reject the null hypothesis. Therefore, we can conclude that not all of the population means of the five programs are equal and that obtaining an
, we find our critical value equal to 4.140. Since our test statistic of 11.19 exceeds our critical value of 4.140, we reject the null hypothesis. Therefore, we can conclude that not all of the population means of the five programs are equal and that obtaining an ![]() -ratio this extreme by chance is highly improbable.
-ratio this extreme by chance is highly improbable.
On the Web
http://preview.tinyurl.com/36j4by6 ![]() -distribution tables with
-distribution tables with ![]() .
.
Technology Note: Calculating a One-Way ANOVA with Excel
Here is the procedure for performing a one-way ANOVA in Excel using this set of data.
Copy and paste the table into an empty Excel worksheet.
Select 'Data Analysis' from the Tools menu and choose 'ANOVA: Single-factor' from the list that appears.
Place the cursor in the 'Input Range' field and select the entire table.
Place the cursor in the 'Output Range' field and click somewhere in a blank cell below the table.
Click 'Labels' only if you have also included the labels in the table. This will cause the names of the predictor variables to be displayed in the table.
Click 'OK', and the results shown below will be displayed.
Anova: Single Factor
Table 5.1
| Groups | Count | Sum | Average | Variance |
| Column 1 | 7 | 22 | 3.142857 | 3.809524 |
| Column 2 | 6 | 33 | 5.5 | 3,5 |
| Column 3 | 8 | 51 | 6.375 | 2.839286 |
| Column 4 | 5 | 38 | 7.6 | 4.3 |
| Column 5 | 6 | 50 | 10 | 2.5 |
Table 5.2
| Source of Variation |
|
|
|
|
|
|
| Between Groups | 150.5033 | 4 | 37.62584 | 11.18893 | 2.05e-05 | 2.742594 |
| Within Groups | 87.43214 | 26 | 3.362775 | |||
| Total | 237.9355 | 30 |
Technology Note: One-Way ANOVA on the TI-83/84 Calculator
Enter raw data from population 1 into L1, population 2 into L2, population 3 into L3, population 4 into L4, and so on.
Now press [STAT], scroll right to TESTS, scroll down to 'ANOVA(', and press [ENTER]. Then enter the lists to produce a command such as 'ANOVA(L1, L2, L3, L4)' and press [ENTER].
When testing multiple independent samples to determine if they come from the same population, we could conduct a series of separate ![]() -tests in order to compare all possible pairs of means. However, a more precise and accurate analysis is the Analysis of Variance (ANOVA).
-tests in order to compare all possible pairs of means. However, a more precise and accurate analysis is the Analysis of Variance (ANOVA).
In ANOVA, we analyze the total variation of the scores, including the variation of the scores within the groups, the variation between the group means, and the total mean of all the groups (also known as the grand mean).
In this analysis, we calculate the ![]() -ratio, which is the total mean of squares between groups divided by the total mean of squares within groups.
-ratio, which is the total mean of squares between groups divided by the total mean of squares within groups.
The total mean of squares within groups is also known as the pooled estimate of the population variance. We find this value by analysis of the standard deviations in each of the samples.
Table 5.3
| Ms. Jones | Mr. Smith | Mrs. White |
| 8 | 23 | 21 |
| 6 | 11 | 21 |
| 4 | 17 | 22 |
| 12 | 16 | 18 |
| 16 | 6 | 14 |
| 17 | 14 | 21 |
| 12 | 15 | 9 |
| 10 | 19 | 11 |
| 11 | 10 | |
| 13 |
(a) State the null hypothesis.
(b) Using the data above, fill out the missing values in the table below.
Table 5.4
| Ms. Jones | Mr. Smith | Mrs. White | Totals | |
|
Number |
8 |
|
||
Total 
|
131 |
|
||
Mean 
|
14.6 |
|
||
Sum of Squared Obs. 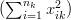
|
|
|||
Sum of Obs. Squared/Number of Obs. 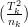
|
|
(c) What is the value of the mean squares between groups, 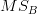 ?
?
(d) What is the value of the mean squares within groups, ![]() ?
?
(e) What is the ![]() -ratio of these two values?
-ratio of these two values?
(f) With ![]() , use the
, use the ![]() -distribution to set a critical value.
-distribution to set a critical value.
(g) What decision would you make regarding the null hypothesis? Why?
In the previous section, we discussed the one-way ANOVA method, which is the procedure for testing the null hypothesis that the population means and variances of a single independent variable are equal. Sometimes, however, we are interested in testing the means and variances of more than one independent variable. Say, for example, that a researcher is interested in determining the effects of different dosages of a dietary supplement on the performance of both males and females on a physical endurance test. The three different dosages of the medicine are low, medium, and high, and the genders are male and female. Analyses of situations with two independent variables, like the one just described, are called two-way ANOVA tests.
Table 5.5
| Dietary Supplement Dosage | Dietary Supplement Dosage | Dietary Supplement Dosage | ||
| Low | Medium | High | Total | |
| Female | 35.6 | 49.4 | 71.8 | 52.3 |
| Male | 55.2 | 92.2 | 110.0 | 85.8 |
| Total | 45.2 | 70.8 | 90.9 |
There are several questions that can be answered by a study like this, such as, "Does the medication improve physical endurance, as measured by the test?" and "Do males and females respond in the same way to the medication?"
While there are similar steps in performing one-way and two-way ANOVA tests, there are also some major differences. In the following sections, we will explore the differences in situations that allow for the one-way or two-way ANOVA methods, the procedure of two-way ANOVA, and the experimental designs associated with this method.
As mentioned in the previous lesson, ANOVA allows us to examine the effect of a single independent variable on a dependent variable (i.e., the effectiveness of a reading program on student achievement). With two-way ANOVA, we are not only able to study the effect of two independent variables (i.e., the effect of dosages and gender on the results of a physical endurance test), but also the interaction between these variables. An example of interaction between the two variables gender and medication is a finding that men and women respond differently to the medication.
We could conduct two separate one-way ANOVA tests to study the effect of two independent variables, but there are several advantages to conducting a two-way ANOVA test.
Efficiency. With simultaneous analysis of two independent variables, the ANOVA test is really carrying out two separate research studies at once.
Control. When including an additional independent variable in the study, we are able to control for that variable. For example, say that we included IQ in the earlier example about the effects of a reading program on student achievement. By including this variable, we are able to determine the effects of various reading programs, the effects of IQ, and the possible interaction between the two.
Interaction. With a two-way ANOVA test, it is possible to investigate the interaction of two or more independent variables. In most real-life scenarios, variables do interact with one another. Therefore, the study of the interaction between independent variables may be just as important as studying the interaction between the independent and dependent variables.
When we perform two separate one-way ANOVA tests, we run the risk of losing these advantages.
There are two kinds of variables in all ANOVA procedures-dependent and independent variables. In one-way ANOVA, we were working with one independent variable and one dependent variable. In two-way ANOVA, there are two independent variables and a single dependent variable. Changes in the dependent variables are assumed to be the result of changes in the independent variables.
In one-way ANOVA, we calculated a ratio that measured the variation between the two variables (dependent and independent). In two-way ANOVA, we need to calculate a ratio that measures not only the variation between the dependent and independent variables, but also the interaction between the two independent variables.
Before, when we performed the one-way ANOVA, we calculated the total variation by determining the variation within groups and the variation between groups. Calculating the total variation in two-way ANOVA is similar, but since we have an additional variable, we need to calculate two more types of variation. Determining the total variation in two-way ANOVA includes calculating: variation within the group (within-cell variation), variation in the dependent variable attributed to one independent variable (variation among the row means), variation in the dependent variable attributed to the other independent variable (variation among the column means), and variation between the independent variables (the interaction effect).
The formulas that we use to calculate these types of variations are very similar to the ones that we used in the one-way ANOVA. For each type of variation, we want to calculate the total sum of squared deviations (also known as the sum of squares) around the grand mean. After we find this total sum of squares, we want to divide it by the number of degrees of freedom to arrive at the mean of squares, which allows us to calculate our final ratio. We could do these calculations by hand, but we have technological tools, such as computer programs like Microsoft Excel and graphing calculators, that can compute these figures much more quickly and accurately than we could manually. In order to perform a two-way ANOVA with a TI-83/84 calculator, you must download a calculator program at the following site: http://www.wku.edu/~david.neal/statistics/advanced/anova2.htm.
The process for determining and evaluating the null hypothesis for the two-way ANOVA is very similar to the same process for the one-way ANOVA. However, for the two-way ANOVA, we have additional hypotheses, due to the additional variables. For two-way ANOVA, we have three null hypotheses:
Let’s take a look at an example of a data set and see how we can interpret the summary tables produced by technological tools to test our hypotheses.
Example: Say that a gym teacher is interested in the effects of the length of an exercise program on the flexibility of male and female students. The teacher randomly selected 48 students (24 males and 24 females) and assigned them to exercise programs of varying lengths (1, 2, or 3 weeks). At the end of the programs, she measured the students' flexibility and recorded the following results. Each cell represents the score of a student:
Table 5.6
| Length of Program | Length of Program | Length of Program | ||
| 1 Week | 2 Weeks | 3 Weeks | ||
| Gender | Females | 32 | 28 | 36 |
| 27 | 31 | 47 | ||
| 22 | 24 | 42 | ||
| 19 | 25 | 35 | ||
| 28 | 26 | 46 | ||
| 23 | 33 | 39 | ||
| 25 | 27 | 43 | ||
| 21 | 25 | 40 | ||
| Males | 18 | 27 | 24 | |
| 22 | 31 | 27 | ||
| 20 | 27 | 33 | ||
| 25 | 25 | 25 | ||
| 16 | 25 | 26 | ||
| 19 | 32 | 30 | ||
| 24 | 26 | 32 | ||
| 31 | 24 | 29 |
Do gender and the length of an exercise program have an effect on the flexibility of students?
Solution:
From these data, we can calculate the following summary statistics:
Table 5.7
| Length of Program | Length of Program | Length of Program | ||||
| 1 Week | 2 Weeks | 3 Weeks | Total | |||
| Gender | Females |
|
8 | 8 | 8 | 24 |
| Mean | 24.6 | 27.4 | 41.0 | 31.0 | ||
| St. Dev. | 4.24 | 3.16 | 4.34 | 8.23 | ||
| Males |
|
8 | 8 | 8 | 24 | |
| Mean | 21.9 | 27.1 | 28.3 | 25.8 | ||
| St. Dev. | 4.76 | 2.90 | 3.28 | 4.56 | ||
| Totals |
|
16 | 16 | 16 | 48 | |
| Mean | 23.3 | 27.3 | 34.6 | 28.4 | ||
| St. Dev. | 4.58 | 2.93 | 7.56 | 7.10 |
As we can see from the tables above, it appears that females have more flexibility than males and that the longer programs are associated with greater flexibility. Also, we can take a look at the standard deviation of each group to get an idea of the variance within groups. This information is helpful, but it is necessary to calculate the test statistic to more fully understand the effects of the independent variables and the interaction between these two variables.
Technology Note: Calculating a Two-Way ANOVA with Excel
Here is the procedure for performing a two-way ANOVA with Excel using this set of data.
Using technological tools, we can generate the following summary table:
Table 5.8
| Source |
|
|
|
|
Critical Value of |
| Rows (gender) | 330.75 | 1 | 330.75 | 22.36 | 4.07 |
| Columns (length) | 1,065.5 | 2 | 532.75 | 36.02 | 3.22 |
| Interaction | 350 | 2 | 175 | 11.83 | 3.22 |
| Within-cell | 621 | 42 | 14.79 | ||
| Total | 2,367.25 |
![]() Statistically significant at
Statistically significant at 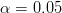 .
.
From this summary table, we can see that all three ![]() -ratios exceed their respective critical values.
-ratios exceed their respective critical values.
This means that we can reject all three null hypotheses and conclude that:
In the population, the mean for males differs from the mean of females.
In the population, the means for the three exercise programs differ.
There is an interaction between the length of the exercise program and the student’s gender.
Technology Note: Two-Way ANOVA on the TI-83/84 Calculator
http://www.wku.edu/~david.neal/statistics/advanced/anova2.html. A program to do a two-way ANOVA on the TI-83/84 Calculator.
Experimental design is the process of taking the time and the effort to organize an experiment so that the data are readily available to answer the questions that are of most interest to the researcher. When conducting an experiment using the ANOVA method, there are several ways that we can design an experiment. The design that we choose depends on the nature of the questions that we are exploring.
In a totally randomized design, the subjects or objects are assigned to treatment groups completely at random. For example, a teacher might randomly assign students into one of three reading programs to examine the effects of the different reading programs on student achievement. Often, the person conducting the experiment will use a computer to randomly assign subjects.
In a randomized block design, subjects or objects are first divided into homogeneous categories before being randomly assigned to a treatment group. For example, if an athletic director was studying the effect of various physical fitness programs on males and females, he would first categorize the randomly selected students into homogeneous categories (males and females) before randomly assigning them to one of the physical fitness programs that he was trying to study.
In ANOVA, we use both randomized design and randomized block design experiments. In one-way ANOVA, we typically use a completely randomized design. By using this design, we can assume that the observed changes are caused by changes in the independent variable. In two-way ANOVA, since we are evaluating the effect of two independent variables, we typically use a randomized block design. Since the subjects are assigned to one group and then another, we are able to evaluate the effects of both variables and the interaction between the two.
With two-way ANOVA, we are not only able to study the effect of two independent variables, but also the interaction between these variables. There are several advantages to conducting a two-way ANOVA, including efficiency, control of variables, and the ability to study the interaction between variables. Determining the total variation in two-way ANOVA includes calculating the following:
Variation within the group (within-cell variation)
Variation in the dependent variable attributed to one independent variable (variation among the row means)
Variation in the dependent variable attributed to the other independent variable (variation among the column means)
Variation between the independent variables (the interaction effect)
It is easier and more accurate to use technological tools, such as computer programs like Microsoft Excel, to calculate the figures needed to evaluate our hypotheses tests.
Table 5.9
| Source |
|
|
|
|
Critical Value of |
| Rows (gender) | 14.832 | 1 | 14.832 | 14.94 | 4.07 |
| Columns (dosage) | 17.120 | 2 | 8.560 | 8.62 | 3.23 |
| Interaction | 2.588 | 2 | 1.294 | 1.30 | 3.23 |
| Within-cell | 41.685 | 42 | 992 | ||
| Total | 76,226 | 47 |
![]()
(a) What are the three hypotheses associated with the two-way ANOVA method?
(b) What are the three null hypotheses for this study?
(c) What are the critical values for each of the three hypotheses? What do these tell us?
(d) Would you reject the null hypotheses? Why or why not?
(e) In your own words, describe what these results tell us about this experiment.
On the Web
http://www.ruf.rice.edu/~lane/stat_sim/two_way/index.html Two-way ANOVA applet that shows how the sums of square total is divided between factors ![]() and
and ![]() , the interaction of
, the interaction of ![]() and
and ![]() , and the error.
, and the error.
http://tinyurl.com/32qaufs Shows partitioning of sums of squares in a one-way analysis of variance.
http://tinyurl.com/djob5t Understanding ANOVA visually. There are no numbers or formulas.
Keywords
ANOVA method
Experimental design
![]() -distribution
-distribution
![]() -Max test
-Max test
![]() -ratio test statistic
-ratio test statistic
Grand mean
Mean squares between groups
Mean squares within groups
Pooled estimate of the population variance
![]()
![]()
Two-way ANOVA