2

La mathématique est une pensée

Cet énoncé n’a aucune évidence. Il a été maintes fois affirmé, d’abord par Platon, qui l’accompagne de toutes sortes de réserves, et maintes fois nié, en particulier par Wittgenstein. Il est sans doute soustrait à toute démonstration. Peut-être est-il le point d’impasse de la mathématisation elle-même, et donc le réel de la mathématique. Mais le réel se déclare plutôt qu’il ne se connaît.

L’obscurité de l’énoncé résulte de ce que semble s’imposer une conception intentionnelle de la pensée : toute pensée, dans cette conception, est pensée d’un objet, qui en détermine l’essence et le style. On pose alors que la mathématique est une pensée dans l’exacte mesure où existent des objets mathématiques, et l’investigation philosophique porte sur la nature et l’origine de ces objets. Or il est clair qu’une telle supposition est problématique : en quel sens les idéalités mathématiques peuvent-elles être déclarées existantes ? Et existantes dans la forme générique de l’objet ? Cette difficulté est examinée tout au long du livre M de la Métaphysique d’Aristote, à propos de ce qu’il nomme les 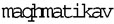, les choses mathématiques, ou corrélats supposés de la science mathématique. La solution d’Aristote est à mon avis définitive, pour autant qu’on aborde la question de la mathématique comme pensée du côté de l’objet ou de l’objectivité. Cette solution s’inscrit entre deux limites.

1. D’une part, il est exclu d’accorder l’être ou l’existence aux objets mathématiques au sens où cet être serait séparé, constituerait un domaine préexistant et autonome de la donation objective. La thèse ici critiquée est attribuée à Platon ; de fait, les réels descendants d’Aristote, c’est-à-dire les empiristes anglo-saxons modernes, appellent « platonisme » la supposition d’une existence séparée et suprasensible des idéalités mathématiques, et font valoir, contre cette supposition, que les objets mathématiques sont construits. Aristote dira alors : les 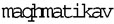ne sont nullement des êtres séparés. Si c’était le cas, il devrait y en avoir une intuition intelligible originaire, que rien n’atteste. Ils ne peuvent donc servir à identifier la mathématique comme pensée singulière. Disons que, pour Aristote, aucune séparation ontologique ne peut garantir la séparation épistémologique ; en particulier, s’agissant de l’écart entre la physique, qui porte sur le sensible, et la mathématique, puisque : « Il est manifestement impossible que les choses mathématiques aient une existence séparée des êtres sensibles » (M, 2, 10).

2. Symétriquement, il est tout aussi impossible que les objets mathématiques soient immanents au sensible. Ce point est traité par Aristote dans le livre B. L’argument principal est que l’immanence d’idéalités indivisibles aux corps sensibles entraînerait l’indivisibilité de ces corps ; ou que l’immanence d’idéalités immobiles entraînerait l’immobilité des corps sensibles. Ce qui répugne à l’expérience. Le fond incontestable de cette thèse est que toute mathématicité immanente soit infecte l’objet mathématique de prédicats sensibles qui lui sont manifestement étrangers, comme la temporalité ou la corruptibilité, soit infecte les corps sensibles de prédicats intelligibles qui leur sont tout aussi étrangers, comme l’éternité ou la transparence conceptuelle.

Au regard du champ de l’expérience, l’objet mathématique n’est donc ni séparé ni inséparable. Il n’est ni transcendant ni immanent. La vérité est qu’il n’a pas d’être à proprement parler. Ou, plus précisément : l’objet mathématique n’existe nulle part en acte. Comme le dira Aristote, ou bien les 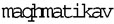n’existent absolument pas, ou bien en tout cas ils n’existent pas d’une manière absolue. Disons que l’objectivité mathématique est un pseudo-être, suspendu entre l’acte pur séparé, dont le nom suprême est Dieu, et les substances sensibles, ou choses réellement existantes. La mathématique n’est ni physique ni métaphysique.

Mais alors, qu’est-ce qu’elle est ? Elle est, en réalité, une activation fictive, là où l’existence en acte fait défaut. L’objectivité mathématique existe en puissance dans le sensible, et y demeure dans la latence définitive de son acte. Ainsi, il est vrai qu’un homme détient en puissance l’un arithmétique, ou qu’un corps détient en puissance telle ou telle forme pure. Ce n’est pas que l’un arithmétique ou la sphère géométrique existent à part, ni qu’ils existent comme tels dans un homme ou une planète. C’est que la pensée peut activer l’un ou la sphère à partir de l’expérience d’un organisme ou d’un objet. Que veut dire activer ? Cela veut dire exactement : traiter comme existant en acte ce qui n’existe qu’en puissance. Traiter comme être un pseudo-être. Traiter comme séparé ce qui ne l’est pas. C’est la définition même d’Aristote : l’arithméticien et le géomètre arrivent, dit-il, à d’excellents résultats « en posant comme séparé ce qui n’est pas séparé ».

Cette fiction a du reste comme conséquence que la norme des mathématiques ne saurait être le vrai, car le vrai ne se laisse pas rejoindre par une fiction. La norme des mathématiques est le beau. Car ce que sépare fictivement le mathématicien, c’est d’abord des relations d’ordre, des symétries, des simplicités conceptuelles transparentes. Or, remarque Aristote, « les formes les plus hautes du beau sont l’ordre, la symétrie, le défini ». Il en résulte que « le beau est l’objet principal des démonstrations mathématiques ».

On peut alors moderniser la conclusion définitive d’Aristote. Il suffit pour cela de se demander : qu’est-ce qui a puissance d’activer l’« être en puissance », ou : qu’est-ce qui a le pouvoir de séparer l’inséparé ? Il est, pour nous modernes, évident que c’est le langage. Comme le remarque Mallarmé dans une citation fameuse, si je dis « une fleur », je la sépare de tout bouquet. Si je dis « soit une sphère », je la sépare de tout objet sphérique. En ce point, mathème et poème sont indiscernables.

On peut alors récapituler la doctrine :

1. La mathématique est la quasi-pensée d’un pseudo-être.

2. Ce pseudo-être est distribué en quasi-objets (par exemple les nombres et les figures, mais aussi bien les structures algébriques, topologiques, etc.).

3. Ces quasi-objets ne sont dotés d’aucune espèce d’existence en acte, n’étant ni transcendants au sensible ni immanents au sensible.

4. Ils sont en fait des créations langagières extirpées fictivement des strates latentes, ou inactivables, ou non séparables, des objets réels.

5. La norme qui régit la fiction séparatrice est la beauté transparente des relations simples qu’elle construit.

6. La mathématique est donc ultimement une esthétique rigoureuse. Elle ne nous dit rien sur l’être-réel, mais elle fictionne à partir de lui une consistance intelligible dont la règle est explicite.

Et enfin :

7. Considérée comme pensée, la mathématique n’est pas pensée de sa pensée. En effet, installée dans sa fiction, elle ne peut qu’y croire. C’est un point sur lequel Lacan insistait à juste titre : le mathématicien est d’abord celui qui croit « dur comme fer » aux mathématiques. La philosophie spontanée du mathématicien est le platonisme, parce que, son acte étant de séparer l’inséparé, il tire de cette activation fictive le spectacle idéel de son résultat. Tout se passe pour lui comme si les objets mathématiques existaient en acte. Plus profondément : la pensée mathématique, comme toute fiction, est un acte. Elle ne peut être que cela, puisqu’il n’y a rien à contempler. Comme le dit Aristote dans une formule très ramassée, dans le cas des mathématiques, 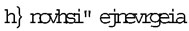, l’intellect est acte. En mathématiques, l’acte qui manque aux objets fait retour du côté du sujet.

Pris dans l’acte d’activation fictive qu’est sa propre pensée, le mathématicien en méconnaît la structure. C’est aussi pourquoi la dimension esthétique est dissimulée sous une prétention cognitive. Le beau est la cause véritable de l’activité mathématique, mais cette cause est, dans le discours mathématique, une cause absente. Elle n’est repérable que par ses effets : « Ce n’est pas une raison parce que les sciences mathématiques ne nomment pas le beau qu’elles n’en traitent pas, car elles en montrent les effets et les rapports. » Il revient au philosophe de nommer la cause réelle de l’acte mathématique, et donc de penser la pensée mathématique selon sa véritable destination.

Cette conception est à mon avis aujourd’hui encore dominante, comme il apparaît à quatre symptômes majeurs :

a) La critique de ce qui est supposé sous le nom de « platonisme » est à peu près consensuelle dans toutes les conceptions contemporaines de la mathématique. De même qu’on y repère les raisons pour lesquelles les mathématiciens sont des platoniciens spontanés, ou « naïfs ».

b) Le caractère construit et langagier des entités ou structures mathématiques est presque universellement admis.

c) Si même l’esthétique n’est pas toujours convoquée comme telle, beaucoup de thèmes courants y sont homogènes. Ainsi, l’absentement de la catégorie de vérité ; la tendance au relativisme (il y aurait plusieurs mathématiques différentes, et en définitive ce serait affaire de goût) ; et enfin l’approche logique des architectures mathématiques, qui les traite comme de grandes formes dont le protocole de construction serait décisif, et dont le référent, ou l’être propre, soit la détermination en pensée de ce qui est pensé, reste inassignable. Conformément à l’orientation d’Aristote, qui reconnaît expressément aux mathématiques une suréminence formelle, ce qu’il appelle une antériorité logique, mais cela pour mieux leur dénier l’antériorité substantielle, ou ontologique. Car, dit-il : « L’antériorité substantielle est le partage des êtres qui, séparés, l’emportent par la faculté de l’existence séparée. » La séparation purement fictive de l’objet mathématique est donc, en dignité ontologique, inférieure à la séparation réelle des choses. A contrario, la transparence logique des mathématiques est esthétiquement supérieure à la substantialité séparée des choses. Ce qui est intégralement reproduit aujourd’hui dans la distinction canonique, elle-même intralangagière, entre les sciences formelles et les sciences empiriques.

d) L’incontestable suprématie, aujourd’hui, de la vision constructiviste, voire intuitionniste, sur la vision formaliste et unifiée du fondement, comme sur l’évidence de la logique classique. Le grand édifice entrepris par Bourbaki était dans une esthétique globale qu’on pourrait dire arborescente. Sur le solide tronc de la logique et d’une théorie homogène des ensembles, poussaient les branches symétriques de l’algèbre et de la topologie, qui se recroisaient en hauteur jusqu’aux structures « concrètes » les plus fines, lesquelles composaient une disposition ramifiée du feuillage. Aujourd’hui, on part plutôt de concrétions déjà complexes, et il s’agit de les plier ou de les déplier selon leur singularité, de trouver le principe de leur déconstruction-reconstruction, sans se soucier d’un plan d’ensemble ou d’un fondement décidé. L’axiomatique est délaissée au profit d’une appréhension mouvante des complexités et des corrélations surprenantes. Le rhizome de Deleuze l’emporte sur l’arbre de Descartes. L’hétérogène donne plus à penser que l’homogène. Une logique intuitionniste ou modale est plus appropriée à cette orientation descriptive que ne l’est la raideur, excluant le tiers, de la logique classique.

La question est donc : quant à la mathématique comme pensée, sommes-nous voués à une version langagière de l’aristotélisme ?

Ce n’est pas ma conviction. L’injonction de la mathématique contemporaine me semble être bien plutôt de relever le platonisme, et d’abord d’en faire comprendre le véritable ressort, entièrement occulté par l’exégèse d’Aristote.

Cependant, au point où nous en sommes, je n’emprunterai pas directement la voie de ce qu’on pourrait appeler la rectification platonicienne. La question dont je voudrais esquisser le traitement est limitée. Puisqu’il s’agit en définitive, posant que la mathématique est une pensée, d’en venir à la pensée de cette pensée, il est pertinent de pointer les moments où la mathématique semble convoquée à se penser elle-même, à dire ce qu’elle est. Ces moments, on le sait, reçoivent le nom conventionnel de « crises », voire de « crises des fondements ».

Ainsi de la crise des irrationnels dans la mathématique dite pythagoricienne, ou de la crise liée aux « paradoxes » de la théorie des ensembles à la fin du siècle dernier, puis aux divers théorèmes de limitation des formalismes découverts dans les années trente. Il y a eu aussi une crise autour du maniement anarchique des infiniment petits au début du XVIII^e siècle, et une autre relative à la géométrie, avec la découverte du caractère indécidable du postulat d’Euclide sur les parallèles.

On a discuté la question de savoir si ces crises étaient intérieures à la mathématique, ou plutôt strictement philosophiques, en important dans le débat entre mathématiciens des options de pensée liées à l’existence de ce que Louis Althusser appelait la « philosophie spontanée des savants ». Althusser soutenait qu’il n’y avait dans les sciences aucune espèce de crise. Il y avait certes des discontinuités, de brusques remaniements qualitatifs. Ces moments étaient de progrès et de création, nullement d’impasse ou de crise. Mais, à l’occasion de ces ruptures, s’engageaient inéluctablement, y compris dans les milieux scientifiques concernés, des luttes de tendances philosophiques, dont l’enjeu était en réalité de redisposer la façon dont les courants philosophiques se servent des sciences pour leurs fins propres, lesquelles, en dernier ressort, sont politiques.

Nous partirons du constat suivant : il y a des moments singuliers où la mathématique semble requise, au regard de ses propres buts, de penser sa pensée. En quoi consiste cette opération ? Tout se joue en fait autour de quelques énoncés sur lesquels la pensée mathématique bute, comme s’ils étaient dans son propre champ la signature de l’impossible.

Ces énoncés sont clairement de trois types :

– Soit il s’agit d’une contradiction formelle, tirée déductivement d’un ensemble de présupposés dont cependant l’évidence et la cohésion semblaient indubitables. C’est la butée sur le paradoxe. Ainsi de la théorie formelle des classes, dans le style de Frege, qui achoppe sur le paradoxe de Russell. L’évidence ici contrainte à l’impossible est celle qui assigne à une propriété quelconque l’ensemble des termes qui possèdent cette propriété. Rien de plus clair que cette doctrine de l’extension d’un concept ; et cependant, comme une épreuve réelle, vient le cas qui affecte cette évidence d’une inconsistance intrinsèque.

– Le deuxième cas est celui où une théorie établie se voit, en un point, diagonalisée par une exception, ou un excès, qui contraint à ne tenir cette théorie, qu’on croyait absolument générale, que pour régionale, voire tout à fait particulière ou restreinte. Ainsi de la démonstration de ce que la diagonale d’un carré est incommensurable à son côté, si on entend par mesure un nombre rationnel. L’évidence de l’assignation à tout rapport saisissable d’une paire de nombres entiers assurait pour les pythagoriciens la réciprocité de l’être et du nombre. Elle est ruinée démonstrativement par un rapport géométrique en excès sur toute paire de nombres entiers qu’on prétendrait lui assigner comme mesure. Il faut donc repenser la pensée où se déployait la numéricité essentielle de l’être, et donc repenser la pensée mathématique comme telle.

– Enfin, le troisième cas est celui où un énoncé inaperçu est isolé comme condition de résultats tenus pour certains, alors que, pris en lui-même, cet énoncé semble insupportable au regard des normes partagées quant aux constructions de la pensée mathématique. Ainsi de l’axiome du choix. Les grands analystes français de la fin du siècle dernier en faisaient implicitement usage dans leurs propres démonstrations ; mais son explicitation formelle leur parut excéder absolument ce qu’ils acceptaient quant au maniement de l’infini ; et surtout, ils y virent une transgression illégitime de la vision constructive qu’ils se faisaient des opérations de la pensée mathématicienne. L’axiome du choix revient en effet à admettre un ensemble infini absolument indéterminé, dont l’existence est affirmée, alors qu’il est langagièrement indéfinissable et, dans la procédure, inconstructible.

On peut donc soutenir que la pensée mathématique revient sur elle-même sous la contrainte d’une butée réelle, ou du surgissement nécessaire, dans son champ, d’un point d’impossible. Cette butée est de l’ordre du paradoxe, qui fait venir l’inconsistance ; de la diagonale, qui fait venir l’excès ; ou du pointage d’un énoncé latent, qui fait venir l’indéfini et l’inconstructible.

Quelle est alors la nature de cette torsion sur elle-même de la mathématique, sous l’injonction de sa butée intérieure ?

Ce qui monte à la surface concerne ce qui, de l’ordre de la pensée mathématique, relève de l’acte, ou de la décision ; et dans le même mouvement, il faut prendre position, puisqu’on est, si je puis dire, au pied de l’acte, sur la norme de la décision qu’il accomplit.

Or, dans tous les cas, dans cette obligation de décider, c’est de l’être qu’il s’agit ; ou du mode sur lequel la mathématique assume pour son propre compte l’énoncé de Parménide : « Le même, lui, est à la fois penser et être. »

Reprenons nos exemples. Pour les Grecs, sous l’injonction de l’incommensurable réel, c’est à la décision d’un autre nouage de l’être et du nombre, du géométrique et de l’arithmétique, que la pensée est astreinte, décision dont le nom propre est Eudoxe. Face au paradoxe de Russell, c’est à une restriction des pouvoirs de la langue sur la détermination du multiple pur qu’il faut se résoudre, décision dont le nom propre est Zermelo. Et quant à l’axiome du choix, c’est à une abrupte décision sur l’infini actuel indéterminé qu’il appelle la pensée, décision qui du reste divise durablement les mathématiciens.

Dans tous les cas, il s’agit de décider en quel sens, et selon la disposition immanente de quelles limites, la pensée mathématique est coextensive à l’être dont sa consistance se soutient.

Nous dirons donc qu’au moment où la mathématique bute sur le paradoxe et l’inconsistance, la diagonale et l’excès, ou encore sur une condition indéfinie, elle en vient à penser ce qui, dans sa pensée, est de l’ordre d’une décision ontologique. Il s’agit proprement d’un acte, qui engage durablement le réel d’être dont elle assumera d’établir les connexions et les configurations. Mais, confrontée ainsi à sa dimension décisoire, la mathématique ne peut qu’être en proie à la question de sa norme, et plus particulièrement : de la norme de ce que la pensée est en état de soutenir comme assertion d’existence. Faut-il faire venir à l’existence des nombres dont le principe n’est plus la composition d’unités ? Faut-il admettre qu’existent des ensembles infinis actuels non dénombrables ? Dans quelles conditions peut-on garantir qu’un concept bien formé admet une extension identifiable ? Comment se nouent l’assertion d’existence et le protocole de construction ? Peut-on admettre qu’existe une configuration intelligible dont il soit impossible d’exhiber un seul cas ? On va trancher ces questions selon une norme immanente qui ne constitue pas la pensée, mais l’oriente.

Nous appellerons orientation dans la pensée ce qui règle dans cette pensée les assertions d’existence. Soit ce qui, formellement, autorise l’inscription d’un quantificateur existentiel en tête d’une formule qui fixe les propriétés qu’on suppose à une région d’être. Ou ce qui, ontologiquement, fixe l’univers de la présentation pure du pensable.

Une orientation dans la pensée s’étend non seulement aux assertions fondatrices, ou aux axiomes, mais aussi aux protocoles démonstratifs, dès que leur enjeu est existentiel. Admettra-t-on, par exemple, qu’on puisse affirmer une existence de cela seul que l’hypothèse d’inexistence conduit à une impasse logique ? C’est le ressort du raisonnement par l’absurde. L’admettre ou non relève, exemplairement, de l’orientation dans la pensée, classique si on l’admet, intuitionniste si on ne l’admet pas. La décision porte alors sur ce que la pensée détermine en elle-même comme voie d’accès à ce qu’elle déclare exister. L’acheminement vers l’existence oriente le cheminement discursif.

Il est à mon sens erroné de dire que deux orientations différentes prescrivent deux mathématiques différentes, soit deux pensées différentes. C’est à l’intérieur d’une pensée unique que s’affrontent les orientations. Aucun mathématicien classique n’a jamais mis en doute la mathématicité reconnaissable de la mathématique intuitionniste. Dans tous les cas, il s’agit de l’identité foncière de la pensée et de l’être. Mais l’existence, qui est à la fois ce que la pensée déclare et ce dont l’être garantit la consistance, est prise selon des orientations différentes. C’est qu’on peut appeler existence ce à propos de quoi décision et rencontre, acte et découverte sont indiscernables. Les orientations dans la pensée visent de façon singulière les conditions de cette indiscernabilité.

On dira donc qu’il y a des moments où la mathématique, butant sur un énoncé qui atteste en un point la venue de l’impossible, se retourne sur les décisions qui l’orientent. Elle saisit alors sa propre pensée, non plus selon son unité démonstrative, mais selon la diversité immanente des orientations dans la pensée. La mathématique pense son unité comme intérieurement exposée à la multiplicité des orientations dans la pensée. Une « crise » de la mathématique est un moment où elle est astreinte à penser sa pensée comme multiplicité immanente de sa propre unité.

C’est en ce point, je crois, et en ce point seulement, que la mathématique, c’est-à-dire l’ontologie, fonctionne comme condition de la philosophie. Disons ceci : la mathématique se rapporte à sa propre pensée selon son orientation. Il revient à la philosophie de poursuivre ce geste, par une théorie générale des orientations dans la pensée. Que toute pensée ne puisse penser son unité que comme exposition à la multiplicité de ce qui l’oriente, c’est là ce dont la mathématique elle-même ne peut rendre compte, mais c’est aussi ce qu’elle manifeste exemplairement. Le rapport complet de la pensée mathématique à sa propre pensée suppose que la philosophie, sous condition des mathématiques, traite la question : qu’est-ce qu’une orientation dans la pensée ? Et plus encore : qu’est-ce qui impose que l’identité de l’être et de la pensée s’effectue selon une multiplicité immanente d’orientations ? Pourquoi faut-il toujours décider quant à ce qui existe ? Car tout le point est que l’existence n’est nullement la donation première. L’existence est précisément l’être même, pour autant que la pensée le décide. Et cette décision oriente essentiellement la pensée.

Il faudrait donc disposer d’une théorie des orientations dans la pensée, comme territoire réel de ce qui peut activer la pensée de la mathématique comme pensée. J’ai, pour mon propre compte, proposé de ce point un traitement sommaire dans L’Être et l’Événement, et je ne peux ici revenir sur sa substructure technique. On y repère trois orientations majeures, identifiables simultanément dans les moments de crise de la mathématique, et dans les remaniements conceptuels de la philosophie. Ces orientations sont l’orientation constructiviste, l’orientation transcendante, l’orientation générique.

La première norme l’existence par des constructions explicites et, en définitive, subordonne le jugement d’existence à des protocoles langagiers finis et contrôlables. Disons que toute existence se soutient d’un algorithme, qui permet d’atteindre effectivement un cas de ce dont il s’agit.

La deuxième, la transcendante, norme l’existence par l’admission de ce qu’on peut appeler une surexistence, ou un point de bouclage hiérarchique qui dispose en deçà de lui-même l’univers de tout ce qui existe. Disons que, cette fois, toute existence s’inscrit dans une totalité qui lui assigne une place.

La troisième pose que l’existence est sans norme, sinon la consistance discursive. Elle privilégie les zones indéfinies, les multiples soustraits à toute récollection prédicative, les points d’excès et les donations soustractives. Disons que toute existence est prise dans une errance qui fait diagonale pour les montages supposés la surprendre.

Il est assez clair que ces trois orientations sont, métaphoriquement, de nature politique. Poser que l’existence doit se montrer selon un algorithme constructif, ou qu’elle est prédisposée dans un Tout, ou qu’elle est une singularité diagonale, cela oriente la pensée selon une acception chaque fois particulière de ce qui est, « ce qui est » étant ici pensé à partir de la décision d’existence. Soit ce qui est est ce dont il y a un cas ; soit ce qui est est une place dans un Tout ; soit ce qui est est ce qui se soustrait à ce qui est. On pourrait dire : politique des particularités empiriques, politique de la totalité transcendante, politique des singularités soustraites. Disons, pour faire court : les démocraties parlementaires, Staline, et, sans doute, ce qui se déclare un peu à tâtons aujourd’hui, une politique générique, une politique de l’existence comme soustraction à l’État, ou de ce qui existe seulement de n’être pas calculable.

Il est magnifique que ces trois orientations soient mathématiquement lisibles, à seulement s’en tenir à la théorie des ensembles. La doctrine des ensembles constructibles de Gödel donne une solide assise à la première, la théorie des grands cardinaux à la seconde, la théorie des ensembles génériques à la troisième.

Mais bien d’autres exemples plus récents nous montreraient comment toute avancée mathématique finit par exposer, dans l’unicité contingente de son mouvement, les trois orientations. Tout mouvement réel est aussitôt la présentation, au point d’être qui y convoque la pensée, des trois orientations. Tout mouvement réel confronte la triplicité formelle des décisions d’existence.

On en retiendra ce point, qui est d’un grand secours dans toutes les situations concrètes : aucune querelle sérieuse entre dispositifs de pensée n’oppose des interprétations à propos d’une existence par tous reconnue. C’est l’inverse qui est vrai : c’est sur l’existence même que l’accord ne se fait pas, car c’est là ce qui fut décidé. Toute pensée est polémique. Mais il ne s’agit nullement d’un conflit des interprétations. Il s’agit d’un conflit des jugements d’existence. C’est pourquoi aucun conflit véritable dans la pensée n’admet de solution ; le consensus est l’ennemi de la pensée, car il prétend que nous partageons l’existence. Mais l’existence est justement, au plus intime de la pensée, l’impartageable.

La mathématique a cette vertu de ne présenter aucune interprétation. Le réel ne s’y montre pas selon le relief des interprétations disparates. Il s’y démontre comme dépourvu de sens. De là que, quand la mathématique se retourne sur sa propre pensée, c’est à nu qu’elle expose les conflits d’existence, et elle nous donne à penser que toute saisie de l’être suppose, quant à l’existence, une décision qui, sans garantie ni arbitrage, oriente décisivement la pensée.

L’éloge par Lautréamont des « mathématiques sévères » est bien ajusté. Ce qu’il y a de sévère n’est pas tant le formalisme, ou l’enchaînement démonstratif, que la mise à nu d’une maxime de pensée qu’on pourrait formuler ainsi : c’est quand tu décides ce qui existe que tu noues ta pensée à l’être. Mais tu es alors, inconscient de l’être, sous l’impératif d’une orientation.