which can be rewritten two ways:
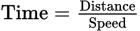and Distance = (Speed)(Time).A rate is a special type of ratio. Instead of relating a part to the whole or to another part, a rate relates one kind of quantity to a completely different kind. When we talk about rates, we usually use the word per, as in “miles per hour,” “cost per item,” etc. Since per means “for one” or “for each,” we express the rates as ratios reduced to a denominator of 1.
The most commonly tested rate on the GRE is speed. This is usually expressed in miles or kilometers per hour. The relationship between speed, distance, and time is given by the formula
which can be rewritten two ways:
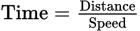and Distance = (Speed)(Time).
Anytime you can find two out of the three elements in this equation, you can find the third.
For example, if a car travels 300 miles in 5 hours, it has averaged
(Note that speeds are usually expressed as averages because they are not necessarily constant. In this example, the car moved at an “average speed” of 60 miles per hour, but probably not at a constant speed of 60 miles per hour.)
Likewise, a rearranged version of the formula can be used to solve for missing speed or time.
Example:
How far do you drive if you travel for 5 hours at 60 miles per hour?
Example:
How much time does it take to drive 300 miles at 60 miles per hour?
Speed is not the only rate that appears on the GRE. For instance, you might get a word problem involving liters per minute or cost per unit. All rate problems, however, can be solved using the speed formula and its variants by conceiving of “speed” as “rate” and “distance” as “quantity.”
Example:
How many hours will it take to fill a 500-liter tank at a rate of 2 liters per minute?
Plug the numbers into our rate formula:
Now convert 250 minutes to hours: 250 minutes ÷ 60 minutes per hour =
hours to fill the tank. (As you can see from this problem, GRE Problem Solving questions test your ability to convert minutes into hours and vice versa. Pay close attention to what units the answer choice must use.)
In some cases, you should use proportions to answer rate questions.
Example:
If 350 widgets cost $20, how much will 1,400 widgets cost at the same rate?
Set up a proportion:
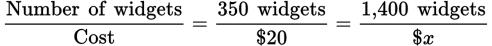
Solving, you will find that x = 80.
So, 1,400 widgets will cost $80 at that rate.
Rates can be added.
Example:
Nelson can mow 200 square meters of lawn per hour. John can mow 100 square meters of lawn per hour. Working simultaneously but independently, how many hours will it take Nelson and John to mow 1,800 square meters of lawn?
Add Nelson’s rate to John’s rate to find the combined rate.
200 m2 per hour + 100 m2 per hour = 300 m2 per hour.
Divide the total lawn area, 1,800 square meters, by the combined rate, 300 square meters per hour, to find the number of required hours, 6.
Proportions can be used to find out how long it takes a number of people (or machines) working together to complete a task. Let’s say we have three people. The first takes a units of time to complete the job. In other words, this person’s rate of work is 1 job per a units of time, or
. The second person takes b units of time to complete the job, and the third c units of time. You can add their rates to find the rate at which they complete the job when they work together. Thus, 
, where T is the time it takes all three people to do the job.
Example:
John can weed the garden in 3 hours. If Mark can weed the garden in 2 hours, how long will it take them to weed the garden at this rate, working independently?
Referring to the formula above, call John’s time per unit of work a and Mark’s time per unit of work b. (There is no need for the variable c, since there are only two people.) Plugging in, you find that
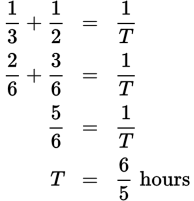
Many students prefer to memorize the following combined work formula, derived from the formula above, for situations in which two people are working together. As above, T is the total amount of time it takes the two people working together to do the job, a is the time it would take one working alone to complete the task, and b the time for the other working alone to complete the task.
This formula is especially handy when the question gives you the times it would take each person to do the job and those times are easy numbers to work with. Let’s take another look at the above example.
Example:
John takes 3 hours to weed the garden, and Mark takes 2 hours to weed the same garden. How long will it take them to weed the garden together?
If there are three entities doing a job together and you are given the times it would take each to do the job alone, you can use an extension of the above formula for this situation.
However, this formula involves so many calculations that adding the rates—using the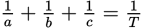 
formula—is often more efficient.
Example:
Our gardeners have decided they are tired of weeding and have purchased three robots that are advertised as being good at gardening. Unfortunately, the robots malfunction a lot. Robot A takes 4 hours, robot B takes 6 hours, and robot C takes 10 hours to weed the garden. How long will it take these robots to weed the garden together?
Solving by adding the rates:
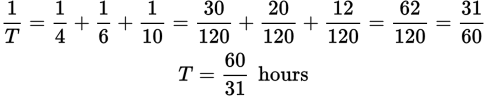
Solving by using the formula:
Whichever way you calculate it, the three robots take just under 2 hours to weed the garden. John and Mark could have done the job faster themselves.
Be familiar with both arrangements of the combined work formula so you can efficiently solve any question, whether the rates or the times are easier to work with.
The average of a group of numbers is defined as the sum of the terms divided by the number of terms.
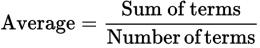
This equation can be rewritten two ways:
Thus, any time you have two out of the three values (average, sum of terms, number of terms), you can find the third.
Example:
Henry buys three items costing $2.00, $1.75, and $1.05. What is the average price (arithmetic mean) of the three items? (Don’t let the phrase arithmetic mean throw you; it’s just another term for average.)
Example:
June pays an average price of $14.50 for 6 articles of clothing. What is the total price of all 6 articles?
Example:
The total weight of the licorice sticks in a jar is 30 ounces. If the average weight of each licorice stick is 2 ounces, how many licorice sticks are there in the jar?
If you’re given the average, the total number of terms, and all but one of the actual numbers, you can find the missing number.
Example:
The average annual rainfall in Boynton for 1976−1979 was 26 inches per year. Boynton received 24 inches of rain in 1976, 30 inches in 1977, and 19 inches in 1978. How many inches of rainfall did Boynton receive in 1979?
You know that total rainfall equals 24 + 30 + 19 + (number of inches of rain in 1979).
You know that the average rainfall was 26 inches per year.
You know that there were 4 years.
So, plug these numbers into any of the three expressions of the average formula to find that Sum of terms = (Average)(Number of terms):
Another way to find a missing number is to understand that the sum of the differences between each term and the mean of the set must equal zero. Plugging in the numbers from the previous problem, for example, we find:
It may be easier to comprehend why this is true by visualizing a balancing, or weighting, process. The combined distance of the numbers above the average from the mean must be balanced with the combined distance of the numbers below the average from the mean.
Example:
The average of 63, 64, 85, and x is 80. What is the value of x?
Think of each value in terms of its position relative to the average, 80.
63 is 17 less than 80.
64 is 16 less than 80.
85 is 5 greater than 80.
So these three terms are a total of 17 + 16 − 5, or 28, less than the average. Therefore, x must be 28 greater than the average to restore the balance at 80. So x = 28 + 80 = 108.
When consecutive numbers are evenly spaced, the average is the middle value. For example, the average of consecutive integers 6, 7, and 8 is 7.
If there is an even number of evenly spaced numbers, there is no single middle value. In that case, the average is midway between (that is, the average of) the middle two values. For example, the average of 5, 10, 15, and 20 is 12.5, midway between the middle values 10 and 15.
Note that not all consecutive numbers are evenly spaced. For instance, consecutive prime numbers arranged in increasing order are not evenly spaced. But you can use the handy technique of finding the middle value whenever you have consecutive integers, consecutive odd or even numbers, consecutive multiples of an integer, or any other consecutive numbers that are evenly spaced.
When there is an equal number of terms in each set, and only when there is an equal number of terms in each set, you can average averages.
For example, suppose there are two bowlers and you must find their average score per game. One has an average score per game of 100, and the other has an average score per game of 200. If both bowlers bowled the same number of games, you can average their averages to find their combined average. Suppose they both bowled 4 games. Their combined average will be equally influenced by both bowlers. Hence, their combined average will be the average of 100 and 200. You can find this quickly by remembering that the quantity above the average and the quantity below the average must be equal. Therefore, the average will be halfway between 100 and 200, which is 150. Or, we could solve using our average formula:
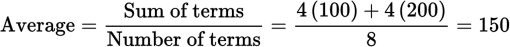
However, if the bowler with the average score of 100 had bowled 4 games and the bowler with the 200 average had bowled 16 games, the combined average would be weighted further toward 200 than toward 100 to reflect the greater influence of the 200 bowler than the 100 bowler upon the total. This is known as a weighted average.
Again, you can solve this by using the concept of a balanced average or by using the average formula.
Since the bowler bowling an average score of 200 bowled
of the games, the combined average will be
of the distance along the number line between 100 and 200, which is 180. Or, you can plug numbers into an average formula to find the following:
Example:
A teacher surprised her students with a 5-question pop quiz. On the quiz, 10% of the students answered no questions correctly, 20% had 2 right answers, 30% answered 3 questions correctly, 30% had 4 right answers, and 10% had a perfect score. What was the weighted average of the number of correct answers?
