Problem Solving Practice Set Answers and Explanations

  1. E

    The other variables all build upon u, so use the Picking Numbers strategy: pick a small number for u and find the values for r, s, and t. For instance, if u = 1, then t = 2u, so t = 2; s = 5t, so s = 10; and r = 3s, so r = 30.

    So, 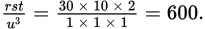The correct answer is (E).

  2. 100

    Since ℓ1 and ℓ2 are parallel, the rules for angles created when parallel lines are cut by a transversal apply. If ∠a has a measure of 40°, then ∠z is also 40°. Because the sum of angles that make up a straight line is 180°, angles d and w are each 180° − 40° =  140°. Furthermore, since vertical (opposite) angles are equal, ∠y is 140° and ∠c is 40°. Thus, d + w − (y + c) =  140 + 140 − (140 + 40) = 280 − 180 = 100.

  3. C
    The question asks for the number of sea lions, and there are fewer sea lions than penguins, so starting small is a good idea. Backsolving works well here. Start with (B). If there are 36 sea lions, then there are 36 + 84 = 120 penguins, and the ratio of sea lions to penguins is This ratio is less than so the answer must be larger. Try (D). If there are 72 sea lions, then there are 72 + 84 = 156 penguins, and the ratio of sea lions to penguins is Since this ratio is too large, the correct answer must be (C).
  4. B, E

    The question asks which numbers have more than two distinct prime factors. Start with 20 and break it down into prime factors: 2 × 2 × 5. Since 20 has only 2 distinct prime factors (2 and 5), (A) can be eliminated. Next, notice that 100 is just 20 × 5, so it has the same two distinct prime factors as 20. (C) can therefore be eliminated. Similarly, 200 is just 100 × 2, so 200 also has the same two distinct prime factors as 20 and 100. Eliminate (D). Now break down 30 into prime factors: 2 × 3 × 5. There are three distinct prime factors here, so (B) is one of the correct answers. Since 210 is 30 × 7, it has four distinct prime factors (2 × 3 × 5 × 7), so (E) is also one of the correct answers.

  5. C

    Each square shares at least one side with another square. That means all of the squares have the same side length. Segment AB would pass through two of the squares, creating two isosceles right triangles in each square. Since each square is the same size, the hypotenuse of each of those triangles would be 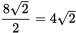 units. Recall that with isosceles right triangles, the ratio of the side lengths is , with 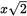representing the hypotenuse. That means the actual hypotenuse of   corresponds to 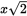, and , representing one side of a square, is 4. There are 10 sides around the perimeter of the figure, so the entire figure has a perimeter of 10 × 4 = 40 units. (C) is the correct answer.

  6. D

    It helps to mark up the figure as you work, so start by redrawing it on your scratch sheet. The area of a rectangle is length × width. The length is the sum of the three top segments: BE + EG + CG = 1.5 + 2 + 1.5 = 5. The width of the rectangle would be the height of triangle AFD less the height of triangle EFG. With an area of x and a base of 2, you can solve for the height of EFG: (2)(h) = x. The height of EFG would be x.

    The height of AFD can be solved by recognizing that triangles EFG and AFD are similar. They share their top angle, and sides AF and DF cut through the parallel lines of the rectangle, creating two sets of corresponding angles. Similar triangles have proportional sides. The base of EFG is 2 and the base of AFD is 5, so the proportion is 2:5. The heights would be in the same proportion: , where h is the height of AFD.  Cross multiply to get 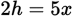. Divide by 2 to solve for h: .

    That means the width of the rectangle would be 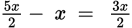. That makes the area of the rectangle  , making (D) the correct answer. 

  7. B

    This question can be deftly handled using the balance approach. The last score was 25, which is 4 points above the final average. That means the previous games must have been a total of 4 points below the final average. The average for each previous game was 20, which is 1 point below the final average. It would take 4 games at 1 point below average to balance out the 4 points above average achieved on the last game. That makes (B) the correct answer. 

    This can also be solved algebraically. Let g represent the number of games she played before last night’s game. If she averaged 20 points per game by then, she scored a total of 20g points. After last night’s game, she played one more game for a total of g + 1 games. She also scored 25 additional points for a total of 20g + 25 points. Her new average is 21, which is found by dividing her current total points by the total number of games she has played:

    Cross multiply to get 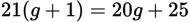. Distribute the 21 to get . From there, isolate g to get g = 4. That means she played 4 games before last night’s game.

  8. C

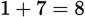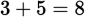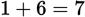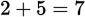    The total number of possible outcomes is the number of possible outcomes from Set A (3) multiplied by the number of possible outcomes from Set B (3). That’s a total of 9 possible outcomes; 5 of those are even ( ; ; ; ; ) and only 2 are prime ( ; ). So, the probability of getting an even result is 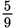, while the probability of getting a prime result is . Subtract those figures to figure out how much greater the probability is of getting an even result: 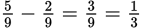. (C) is the correct answer.

    Note that (D) is a trap for those who only look at the possible sums. There are five distinct sums that are possible: 6, 7, 8, 9, 10. However, there is only one way that a sum of 6 can result (1 + 5), while there are two ways that a sum of 7 can result (1 + 6 and 2 + 5). Thus, the probability of getting each sum is not the same. Each individual outcome of selecting a number from each set must be considered.

  9. C

    With smaller numbers, it would be straightforward to simply list out all of the positive factors and count how many were odd. With 768, however, that would be overly time-consuming. Remember, though, that any non-prime number greater than 1 can be expressed as the product of prime factors, and finding prime factors is more manageable, even with large numbers.

    A prime factor tree would show that the prime factorization of 768 consists of eight 2s and a 3. Since multiplying the 3 by any combination of 2s would result in an even factor, 3 itself is the only positive odd factor that can be generated through prime factorization. (B), however, is a trap for those who forget that 1 is a factor of every number. 768 thus has two positive odd factors, 1 and 3, and (C) is the correct answer.

  10. B

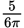    The distance covered in a full lap around the circle would be equal to the circumference of that circle. The circumference of a circle is equal to . With a radius of , the circumference of the circular path is .

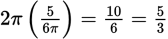    If Evan ran t times around the path, the total distance run would be . Evan ran a total of 5 km, so . Divide both sides by to get t = 3, which means Evan ran 3 times around the path. (B) is the correct answer.