Quantitative Reasoning Practice Set 2 Answers and Explanations

  1. A
    This question requires no computation but only a general understanding of how averages work and what the word “median” means. The median of a group of numbers is the “middle number”; it is the value above which half of the numbers in the group fall and below which the other half fall. If you have an even number of values, the median is the average of the two “middle” numbers; if you have an odd number of values, the median is one of the values. Here, in Quantity B, the median is 101. In Quantity A, if the numbers were 100, 101, and 102, then the average would also be 101, but because the third number, 103, is greater than 102, then the average must be greater than 101. Quantity A is greater than 101, and Quantity B equals 101; Quantity A is larger.
  2. A
    Start with the information you are given. You know that the length of the chord is 15. What does that mean? Well, because you don’t know exactly where A and B are, it doesn’t mean too much, but it does tell you that the distance between two points on the circle is 15. That tells you that the diameter must be at least 15. If the diameter were less than 15, then you couldn’t have a chord that was equal to 15, because the diameter is always the longest chord in a circle. The diameter of the circle is 15 or greater, so the circumference must be at least 15π. That means that Quantity A must be larger than Quantity B.
  3. C

    The equation in the centered information looks complicated, but we’ll take it one step at a time. Because Quantity A has only h in it, solve the equation for h, leaving h on one side of the equal sign and r on the other side. First, substitute the value for x into the equation; then solve for h in terms of r.

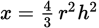
    Substitute 1 for x.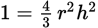
    Divide both sides by
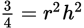
    Take the positive square root of both sides, using the information that r and h are positive.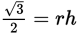
    Divide both sides by r to get h alone.
    The two quantities are equal.
  4. C

    Draw an xy-plane and label the points given to help solve this problem. You know where points B and C are; they’re on the x-axis. You don’t know where A is, however, which may make you think that the answer is choice (D). But you’re given more information: you know that the triangle has an area of 18. The area of any triangle is one-half the product of the base and the height. Make side BC the base of the triangle; you know the coordinates of both points, so you can find their distance apart, which is the length of that side. C is at the origin, the point (0,0); B is at the point (6,0). The distance between them is the distance from 0 to 6 along the x-axis, or just 6. So that’s the base. What about the height? Because you know that the area is 18, you can plug what you know into the area formula.

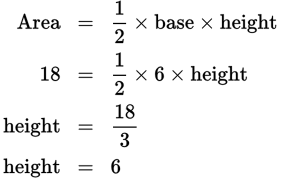
    That’s the other dimension of the triangle. The height is the distance between the x-axis and point A. Now you know that A must be somewhere in the first quadrant, since both the x- and y-coordinates are positive. Don’t worry about the x-coordinate of the point, because that’s not what’s being compared; you care only about the value of y. You know that the distance from the x-axis to the point is 6, because that’s the height of the triangle, and that y must be positive. Therefore, the y-coordinate of the point must be 6. That’s what the y-coordinate is: a measure of the point’s vertical distance from the x-axis. (Note that if you hadn’t been told that y was positive, there would be two possible values for y: 6 and −6. A point that’s 6 units below the x-axis would also give a triangle with height 6.) You still don’t know the x-coordinate of the point, and in fact you can’t figure that out, but you don’t care. You know that y is 6; therefore, the two quantities are equal.

  5. D

    With symbolism problems like this, it sometimes helps to put the definition of the symbol into words. For this symbol, you can say something like “x Φ y means take the sum of the two numbers and divide that by the difference of the two numbers.” One good way to do this problem is to Pick Numbers. You know that p is positive and q is negative. So suppose p is 1 and q is −1. Figure out what p Φ q is first. You start by taking the sum of the numbers, or 1 + (−1) = 0. That’s the numerator of the fraction, and you don’t really need to go any further than that. Whatever their difference is, because the numerator is 0, the whole fraction must equal 0. (The difference can’t be 0 also, since p ≠ q.) So that’s p Φ q. Now what about q Φ p? Well, that’s going to have the same numerator as p Φ q: 0. The only thing that changes when you reverse the order of the numbers is the denominator of the fraction. So q Φ p has a numerator of 0, and that fraction must equal 0 as well.

    So you’ve found a case where the quantities are equal. Try another set of values and see whether the quantities are always equal. If p = 1 and q = −2, then the sum of the numbers is 1 + (−2) or −1. So that’s the numerator of the fraction in each quantity. Now for the denominator of p Φ q, you need p − q = 1 − (−2) = 1 + 2 = 3. Then the value of p Φ q is 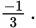The denominator of q Φ p is q − p = −2 − 1 = −3. In that case, the value of q Φ p is 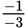or The relationship between quantities is different; therefore, the answer is (D).

  6. D

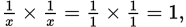    Picking Numbers will help you solve this problem. For and so Quantity A is larger. For and so Quantity B is larger. The relationship between quantities is different; therefore, the answer is (D).

  7. B

    The sum of the interior angles of a triangle is 180°. One of the angles of the large triangle formed by the outside perimeter is a right angle, or 90° angle. The remaining 90° must come from the sum of x, y, and the angle adjacent to y. Therefore, the sum of x and y alone must be less than 90°. Quantity B is greater, making the answer (B).

  8. A

    You could solve this system of equations by substitution or combination. To use combination, multiply all the terms of t − s = −4 by 4 to get −4s + 4t = −16. Now add this result to the other equation:

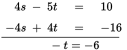
    So t = 6. Plug this value into the second equation: 6 − s = −4, to get s = 10. Thus, Quantity A is greater, and (A) is correct.

  9. D
    Divide both sides of the inequality by 6. You’re left with (10)n > 10,001. The number 10,001 can also be written as 104 + 1, so you know that (10)n > 104 + 1. Therefore, Quantity A, n, must be 5 or greater. Quantity B is 6. Because n could be less than, equal to, or greater than 6, you need more information.
  10. B
    Try to set the quantities equal. Could the tens digit of y be 4? If it is, and the thousands digit is 2.5 times the units digit, then the thousands digit must be  . . . 10? That can’t be right. A digit must be one of the integers 0–9; 10 isn’t a digit. Therefore, 4 is too big to be the tens digit of y. In fact, the only possible value for the tens digit of y is 2. Quantity B is greater than Quantity A.
  11. D
    To find the average, add the quantities together and divide by 4: (2x + 3) + (5x − 4) + (6x − 6) + (3x − 1) = 16x − 8 and The correct choice is (D).
  12. E
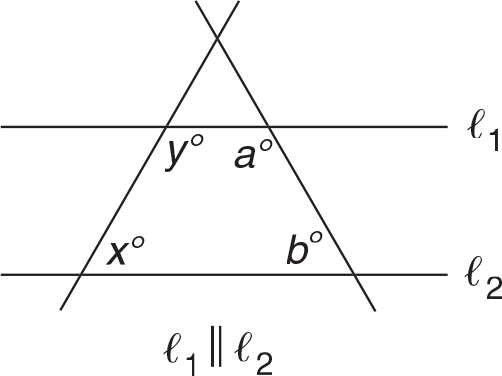
    Parallel lines l1 and l2 are cut by two transversal lines, intersecting at a point above l1, forming a triangle. Four angles, x, y, a, and b degrees, are formed inside the transversal lines and between l1 and l2. Angle y is formed by the intersection of l1 and the transversal line on the left, angle x is formed by the intersection of l2 and the transversal line on the left, angle a is formed by the intersection of l1 and the transversal line on the right, and angle b is formed by the intersection of l2 and the transversal line on the right.

    When a transversal cuts a pair of parallel lines, in this case ℓ1 and ℓ2, the angles are always supplementary and their sum is 180. So, the sum (x + y) is equal to the sum (a + b). The exact values of the individual angle measures cannot be determined from the figure. The answer is (E).

  13. D
    First, find the value of x, using the fact that there are 180° in a straight line. Set the sum of the angle measures equal to 180: 5x + 4x + 3x = 180, 12x = 180, and x = 15. Angle SRU equals 4x + 5x = 9x, which is 135°. Choice (D) is correct.
  14. B, C, D, E
    You know that the ratio of oranges to apples is 9 to 10 and that there are at least 200 apples. The ratio tells you that there are more apples than oranges. At the minimum, there must be 180 oranges to satisfy the proportion 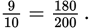There could be more than 200 apples, so any number of oranges greater than 180 for which the ratio 9:10 applies is also correct. All of the choices are multiples of 9, so the correct choices are (B), (C), (D), and (E).
  15. C, D, E

    The area of the shaded region is the area of the square minus the area of the portion of the circle that is inside the square. The area of a square is its side squared. The area of square ABCD is 42 = 4 × 4, which is 16. Now find the area of the portion of the circle that is inside the square. Because the diameter of the circle is a side of the square, you know that exactly one-half of the circle’s area is inside the square. Also, because the diameter of the circle is twice the radius, the radius of the circle is or 2. The area of a circle with a radius r is πr2. The area of the complete circle in this question is π(22), which is 4π. So half the area of this circle is 2π. Thus, the area of the shaded region is 16 − 2π.

    That means that 16 − 4π and 16 − 16π are less than 16 − 2π, so they cannot be correct choices. However, the sum of 16 and any positive number is greater than 16 and also greater than 16 − 2π. So, the correct choices are (C), (D), and (E).

  16. 8

    Simplify each inequality to restate them in terms of x and y. Divide all the terms of −30 ≤ 6x ≤ 60 by 6 to get −5 ≤ x ≤ 10. To simplify 40 ≥  2y + 4  ≥  8, subtract 4 from each term to get 36 ≥ 2y ≥ 4. Then, divide through by 2 to see that 18 ≥ y ≥ 2. The maximum value of x − y will be the greatest possible value of x minus the least possible value of y. This is 10 − 2, so the correct answer is 8.

  17. D

    Although there are 6 numbers on the die, when it comes to evens and odds, there are only two outcomes of a roll. Thus, for three rolls, there are 2 × 2 × 2 = 8 equally possible outcomes: EEE, EEO, EOE, EOO, OOO, OOE, OEO, and OEE. Three of these, EOO, OOE, and OEO, result in exactly one even number.  Use the probability formula  to determine the probability, which is . The decimal equivalent  is 0.375, so (D) is correct.

  18. B

    The first graph shows the beginning and ending prices. Start by “eyeballing” the two bars for each of the five funds. Fund E was flat, so eliminate that one. Fund D had a slight increase, but, since the question asks for the greatest percent increase and Fund D had a relatively high beginning price, it does not have the greatest percent increase.

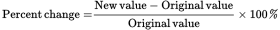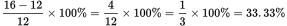    You might be able to infer that Fund B had the greatest percent increase since its starting value was less than those of Fund A and Fund C, but here are the calculations to confirm that. Use the percent change formula to compare the increases of these three funds: . Fund A had an original price of $24 and a new price of $28, so the percent change was . For Fund B:  . For Fund C: 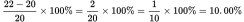 . So, Fund B had the greatest percentage increase, and (B) is correct.

  19. 50,000

    Extract the per share prices of the two funds from the first chart and multiply each by the number of shares shown on the second chart. For Fund C, that is $20/share × 1,000 shares = $20,000. For Fund E, the value is $50/share × 600 shares = $30,000. Thus, the total is $20,000 + $30,000 = $50,000.

  20. A

    The dollar value increase of each fund is the price increase per share times the number of shares held. For Fund A, that was ($28 − $24)(600) = ($4)(600) = $2,400. Fund B increased by ($16 − $12)(500) = ($4)(500) = $2,000. The increase in Fund C was ($22 − $20)(1000) = ($2)(1000) = $2,000. The value of the investment in Fund D increased by ($42 − $40)(300) = ($2)(300) = $600. Fund E’s price did not increase, so the correct choice is (A).