Counting Methods and Probability Practice  SET Answers and Explanations

  1. Basic

  2. 120
    Since the books are just being put in a suitcase, order doesn’t matter, and the combinations formula can be used.
  3. 360
    Here, order does matter since the candles are distinctly colored and being placed into slots on the candelabras. There are 6 possible candles for the first slot, 5 for the second, 4 for the third, and 3 for the 4th. To find the total number of possibilities, multiply each of the possibilities for the four slots together (6 x 5 x 4 x 3) to get 360.
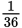
  4. There are 6 equally likely outcomes for one roll of a fair die. One of these outcomes is 6, so the probability of rolling a 6 is . The question asks for the probability of rolling a 6 on the first roll and the probability of rolling a 6 on the second roll. These events are independent, so multiply the two probabilities:  .
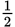
  5. A roll of 2 or 4 or 6 would meet the criterion in the question. These are mutually exclusive outcomes, so add their probabilities:  .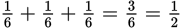
  6. 18
    The number of options Pablo has for the beverage is simply 3, because he can only select one item of the 3 that are available to him. To calculate the number of options for the grain bars, use the combinations formula, because the order in which Pablo selects the 2 grain bars does not matter:  . Since Pablo gets to choose a beverage and two grain bars, and for each of the 3 beverages he can choose from 6 different options of grain bars, multiply the two numbers of choices: 3 × 6 = 18.

  7. Intermediate

  8. 9
    The formula based on the inclusion-exclusion principle for sets states that 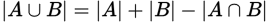  . Substitute the numbers given in the question:   .
  9. There are two possible outcomes for each flip of the coin: heads or tails. You might be tempted to think that the total number of possible outcomes for 4 consecutive flips would be 4 × 2 = 8, but remember that the coin is flipped once and then a second time and then a third time and then a fourth time, so the total number of possible outcomes is actually 24 = 16. If only one head is the result, that could occur on any one of the 4 flips, so there are 4 desired outcomes. The probability is thus  .
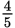
  10. The most efficient way to approach this question is to determine the probability that Latisha will not draw a blue marble in 3 attempts and subtract that from 1 to get the probability that she will. There are 6 total marbles, of which 4 are not blue, so the probability that Latisha will not draw a blue marble on the first attempt is 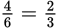 . For the second attempt there will only be 5 marbles remaining, 3 of which are not blue, so the probability of not drawing a blue marble on the second attempt is  . By the time Latisha tries a third time, there will be 2 blue marbles among the 4 that are left, so the probability of drawing a marble that is not blue is 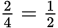. In order not to draw any blue marbles, Latisha will have to be unsuccessful on the first and second and third attempts, so the probability of that happening is 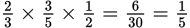. Therefore, the probability that Latisha will be successful is .
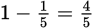  11. 12
    The formula for overlapping sets is Total = Group A + Group B – Both + Neither. Since the question defines crossover as country and pop, the rock songs can be considered “neither.” Plug the given values into the equation: 60 = 30 + 18 – Crossover + 24. Add Crossover to both sides of the equation and subtract 60 from both sides to get: Crossover = 30 + 18 + 24 – 60 = 12.
  12. 6
    After 1 blue chip was removed, there were 9 chips left. If the probability of drawing another blue chip from those remaining 9 was then , there must have been  x 9 = 3 blue chips, and 9 – 3 =  6 red chips remaining. Since no red chips were drawn, the original number of red chips must also have been 6.

  13. Advanced

  14. 30%
    Set up a table to organize the information and derive the values needed to answer this overlapping sets question. The question states that 60% was the total count for A. Put that at the bottom of the “For A” column. The question further states that two-thirds of those voters, which is 40%, also voted for B, so enter that value in the chart as well, at the top of the “For A” column. The total of all the categories must be 100%, as shown in the bottom right cell of the table. Now use these figures to calculate other cells. If 60% of the total voted for A, then 40% of the total did not vote for A. That goes at the bottom of the “Not for A” column. The question does not state what percentage voted for B, but it does mention that B was “chosen by a majority,” so enter >50% in the Total column, in the “For B” row. Since 40% of that total is already represented in the “For B/For A” cell, the “For B/Not for A” cell must be greater than 10%, so enter that in the table. Finally, look at the middle cell. If 40% of the total did not vote for A, and at least 10% were “For B,” then less than 30% did not vote for either A or B. Put that in the middle cell.                                                                                                                                                                                
    T

    		For A Not for A Total
    For B 40% >10% >50%
    Not for B
    		<30%
    Total 60% 40% 100%
  15. 60
    This question represents a pattern of a counting problem with certain conditions or restrictions added. There are 6! ways to arrange 6 different items. However, in this case, many of those arrangements will appear identical. Consider the configuration in the question, AAABBC. If the A’s were not identical there would be 3! = 6 different-appearing ways to arrange them. However, since the A’s are identical, all 6 of those arrangements have the same appearance. So the number of arrangements must be reduced by a factor of 6. Similarly, there are 2 identical ways to set up any configuration of the B’s. The number of different-appearing arrangements is thus . This simplifies to .
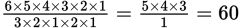  16. 288
    This question involves the “groups of groups” pattern. First consider how many ways the groups (squads) can be arranged. Since there are 3 distinct squads, that is 3! = 3 × 2 × 1 = 6 different ways. For the squad that is permitted to choose any order they wish, there are 4! = 4 × 3 × 2 × 1 = 24 different ways they can line up. The squad that lines up by height can only have 2 variations and the remaining squad only has one way to line up within the squad. Therefore, the total number of ways that the platoon can line up is 6 × 24 × 2 × 1 = 288.                               
  17. 0.6
    Use the formula for two independent events to calculate the probability that event B occurs. Designate the probability that A occurs as PA, that B occurs as PB, and the probability that at least one occurs as PA or B. From the question, PA = 0.5 and PA or B = 0.8. The formula for PA or B is: PA or B = PA + PB – PA and B. Since the events are independent, PA and B = PA × PB. Thus, the formula can be written as PA or B = PA+ PB – (PA× PB). Plug in the known values to get:

    An alternative approach to this question would be to use the fact that the probability of neither event occurring is 1 – 0.8 = 0.2. Since this is equivalent to PNot A × PNot B, set up the equation: 0.2 = (1.0 – 0.5) × PNot B. So 0.4 is PNot B and 0.6 is PB.

  18. The desired outcome is R-S-T in any order. The probability of rolling an R (PR) on any roll is . Similarly, PS =  and PT = . Thus the probability of rolling one of each is . There are 3! = 6 different orders in which R-S-T can be rolled, so the total probability of rolling R-S-T in any order is .