Answers and Explanations

Quantitative Reasoning 2

  1. C

    The perimeter of isosceles triangle ABC is 32, the length of one side is 10, and the height is 8. Your job is to compare the longest side of the triangle to 12. There are two ways to create an isosceles triangle with perimeter 32 and one side of length 10. In one scenario, there are two sides each 10 units long. In this case, the remaining side will be 32 − 10 − 10 = 12 units long, and the triangle will look like this sketch: 

    In this instance, the height bisects the base of ΔABC to create two right triangles, each with a short leg of 6 and a hypotenuse of 10. So these are 3:4:5 right triangles with sides of 6, 8, and 10. Thus, the height of ΔABC, as stated in the centered information, is 8, and it follows that sides of 10, 10, and 12 are allowable for ΔABC under the constraints provided. The length of the longest side of ΔABC is 12, and the two Quantities are equal. 

    In the second scenario, the side with length 10 is the side that does not match another side. In this case, the total length of the two equal sides must be 32 − 10 = 22, which means each of the matching sides is half that, 11. So this time, ΔABC would be divided into right triangles with one side equal to 5 and a hypotenuse of 11.

    Using the Pythagorean theorem, h2 + 52 = 112. So, h2 = 121 – 25 = 96. Thus, the height of this triangle is 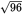. However, the centered information states that the height is 8; therefore, the equal sides can’t be 11. Instead, the equal sides of ΔABC are 10, and the longest side is 12, as shown in the first sketch; (C) is correct.

  2. A

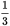    The centered information is a function of the variable z.  The comparison is between the value of the function when z is  and the number 2. Plug  in for z and evaluate the function:    . When dividing by a fraction, invert the fraction and multiply. So, 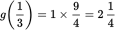  . Since this is greater than 2, (A) is correct.

  3. B

    The centered information provides the distance between two cities and the average speeds between the two cities when traveling by plane and by train. Quantity A is just a way of saying how much longer it takes to travel from A to B by train than by plane. Quantity B is 330 minutes.

    Use the basic formula Rate × Time = Distance rearranged to 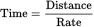. For the plane, that is 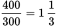  hours. For the train, the time is   hours. The difference is 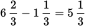 hours. Converted to minutes, that is  minutes. (B) is correct.

    Alternatively, you could have converted the two speeds to miles per minute by dividing the speeds in miles per hour by 60. The plane’s speed was 300 ÷ 60 = 5 miles per minute, and the train’s speed was 1 mile per minute. Thus, the plane took 400 ÷ 5 = 80 minutes, and the train made the journey in 400 ÷ 1 = 400 minutes. The difference between the two is 320 minutes. 

  4. A

    The centered information describes two raises that Navid received in two separate years. The first raise was $10,000 and the second was $10,800. Quantity A represents the percent increase of the first raise and Quantity B the percent increase of the second. Be careful here. While the second raise may have a greater dollar amount, it may not have been a greater percent increase, since each percent increase is based on a different starting value.

    The percent increase formula is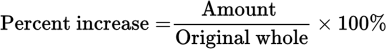                              
    Start by finding the percent increase in 2015: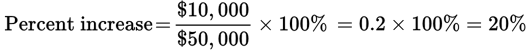
    Now, find the percent increase for 2017: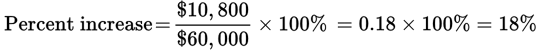 
    Thus, despite the fact that the dollar value of the 2017 raise was greater, the 2015 raise was actually a bigger percent increase. Quantity A is greater, so the answer is (A).

  5. A

    Remember that geometry figures need not be drawn to scale on the GRE, so avoid the temptation to answer the question based on the appearance of the diagram. Since angle ACB makes a straight line along with n, and n = 120°, angle ACB must be 60°. Since 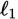  and  are parallel, all acute angles formed by a transversal are equal, as well as all obtuse angles. Notice that angle ABC makes a straight line along with one of these obtuse angles; this obtuse angle must therefore be equal to m, so it’s also 150°. Thus, angle ABC is 30°. This means that triangle ABC is a 30°-60°-90° triangle, and its side lengths have the ratio , where x is the side opposite the 30° angle. In this triangle, that’s AC. So AC = x and AB = , and although there’s no way to find out the value of x, AB must be bigger; (A) is correct. It’s also possible to get to this answer without using the 30°-60°-90° side ratio because in a triangle, a side opposite a larger angle will be longer than a side opposite a smaller angle.

  6. A

    The centered information shows line segment RT with a total length of 4 divided into segments y and z where 3y − z  =  8. The comparison is between the length of segment RS, which is y, and 2.5. Since the total length of the line segment is 4, you can write the equation y + z = 4. Now, you have two variables and two distinct linear equations. Add the two equations: 

    Since 3 > 2.5, (A) is correct.

  7. D

    To make the comparison easier to work with, manipulate the given inequality so that x and z are on the left side and −y is on the right, just as it is in Quantity A on the left and Quantity B on the right. Subtract z and y from both sides of the centered inequality: 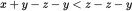  simplifies to 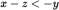 . If x is negative, then 2x − z is even less than x − z, so Quantity B would be greater. However, if, for instance, x = 2, y = 1, and z = 4, then x − z < −y, so these values are permissible, but  . So, for those values, Quantity A is greater. (D) is correct.

  8. C

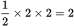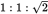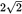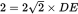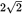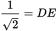    The area of a triangle equals , which for ΔABE is . Furthermore, since ΔABE is a right isosceles, the ratio of the sides is . Because the equal sides are 2, the hypotenuse, BE, is . The area of a rectangle is base × height. In this case, that is BE × DE. Plug in the known values: . Divide both sides by  to get , which simplifies to . Thus, the ratio of BE to DE is 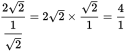 . This is equivalent to 4:1, so (C) is correct.

  9. C

    The formula for the circumference of a circle is π × diameter. If the circumference of each circle in the figure is 8π, the diameter of each circle is 8, and the radius is 4. Each side of triangle PQR consists of the full diameter of the circle in the middle plus the radii of the two circles on the ends. For example, side RP consists of the radius of the circle with center R, the diameter of the middle circle above that, and the radius of the circle with center P. Thus, side RP has a length of 4 + 8 + 4 = 16. Since each side of the triangle passes through the same number of radii, each side has the same length. The perimeter of the entire triangle is therefore 16 × 3 = 48. The correct answer is (C).

  10. D

    Begin by dealing with the negative exponent in the fraction. To handle a negative exponent, take the reciprocal of the base to the positive value of the exponent. In other words, 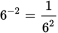. That means  . The equation then becomes 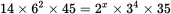. At this point, rather than multiplying and dividing with the calculator, break the numbers down into their prime factors. This will keep the numbers small and make it easier to see how the exponents fit in. The result is  . Expand the exponents to get 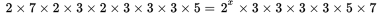 . Now divide both sides by all of the common prime factors. Do this  simply by crossing off the prime factors that appear on both sides, as follows: 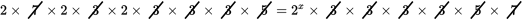What remains is 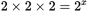. Thus x = 3, and (D) is the correct answer.

  11. C

    The question provides only one equation with two variables, but it asks for the value of the ratio of those two variables rather than the values of the variables themselves. This question could not ask for the value of each variable since it provides only one distinct equation with two variables. It is possible, however, to solve for the ratio of the variables. Start by simplifying the right side: . Cross multiply to get rid of the fractions: 5(w – z) = –12w. And, distribute: 5w – 5z = –12w. Then, add 12w and 5z to both sides to get 17w = 5z. Finally, divide both sides by z and by 17: . (C) is correct.

  12. 0.4

    The figure can be divided into a right triangle on top of a trapezoid. Use the numbers on the grid to calculate the dimensions of the triangle and the trapezoid. The base of the triangle extends to the left from point B (2.0,−1.2) to the point where a horizontal line would intersect line AB at (1.4,−1.2). The height of the triangle is the distance from this point to point A (1.4,−0.8). So the length of the base is |2.0 − 1.4| = 0.6 and the height is |−0.8 − (−1.2)| = 0.4. Use the equation for the area of a triangle: .

    The upper parallel side of the trapezoid is the base of the triangle, which is 0.6 long. The lower parallel side is line DC, so the length of that side is |2.2 − 1.4| = 0.8. The height of the trapezoid is |−1.2 −(−1.6)| = 0.4. Use the formula for the area of a trapezoid: 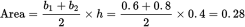 . So the total area of the figure is 0.12 + 0.28 = 0.4 square units.

  13. C

    The question asks for the number that is 40% less than 1.25 × 104, which is 12,500. To minimize calculation, find 100% − 40% = 60% of 12,500: 0.60 × 12,500 = 7,500. In scientific notation, this is 7.5 × 103, which is (C).

  14. A, D

    The right answer(s) for this question must have an odd number of factors in order to be divisible by an odd number of different positive integers. First, eliminate any prime numbers since they are divisible only by themselves and 1. (B) 17 is a prime number. Now check the remaining choices. The factors of 9 are 1, 3, and 9, so (A) is a correct choice. The factors of 24 are 1, 2, 3, 4, 6, 8, 12, and 24 for a total of 8, so eliminate (C). The distinct factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36 for a total of 9, so (D) is a correct choice. Finally, the factors of 42 are 1, 2, 3, 6, 7, 14, 21, and 42. Since there are 8 factors, (E) is incorrect. The correct choices are (A) and (D). 

    Perhaps you noticed that both correct answers are perfect squares. That is because the numbers that are not perfect squares have pairs of factors and thus an even number of factors, but a perfect square has one single factor that is the square root, thereby creating an odd number of factors. If you make this connection initially, you can quickly identify the correct choices.

  15. 3

    Triangle ABC is a right triangle with a short side of 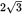 cm and a hypotenuse of cm. Because the short side is half the hypotenuse, this is a 30°-60°-90° triangle with the 30° angle at vertex A. The ratio of the sides of this triangle are 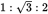, so side AB is . 

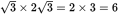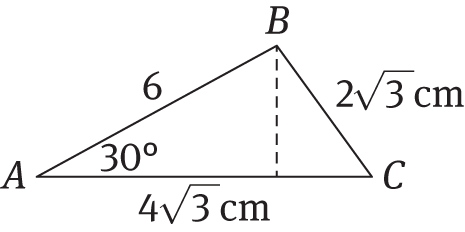
    Triangle ABC with a perpendicular line drawn from vertex B to side AC. Side BC is equal to 2 square root of 3 , sides AC is equal to 4 square root of 3 , and side AB is 6. The angle at vertex A is 30 degrees.

    A perpendicular from B to line AC creates two more 30°-60°-90° triangles. In the triangle on the left, the perpendicular is the short side and the hypotenuse is 6. The length of the perpendicular is half the length of the hypotenuse, or 3.

  16. C

    Rearrange the formula 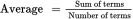to Sum of terms = Average × Number of terms. The sum of all three numbers is 3(5a − 2) = 15a − 6. The average of the other two numbers is 4a + 2b + 1, so their total is twice that, or 8a + 4b + 2. The remaining number must be the difference between these totals: 15a − 6 − (8a + 4b + 2) = 15a − 6 − 8a − 4b − 2 = 7a − 4b − 8. (C) is correct.

  17. B, DEBE

    Test each point. Substitute a value for x and compare the result to the given value for y in the ordered pair.

    (A) Let x = −5.

    (B) Let x = −4.

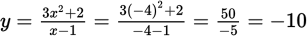
    (C) Let x = 0.

    (D) Let x = 3.

    (E) Let x = 5.

    The correct answers are (B) and (D).

  18. E

    Since there are more males than females in all of the age brackets on the graph, the ratio of male lawyers to female lawyers will be the lowest where the two lines on the double line graph are the closest. Skimming the line graph, you can see that at Over 70 the lines almost overlap, so (E) Over 70 is the correct answer.

  19. B

    The starting point for this question is finding the number of lawyers under the age of 30. The line graph places the number of male lawyers under age 30 right at 100,000, while the number of female lawyers under age 30 is a little above the halfway point between 50,000 and 100,000, or approximately 75,000, which means there were about 100,000 + 75,000, or 175,000 lawyers under the age of 30 in 2015. The pie chart shows that 7% of the lawyers are intellectual property lawyers, so 175,000 × 0.07 =  12,250. Now, if 26% of the intellectual property lawyers specialize in industrial property, the remaining almost 75% must specialize in copyright law. Estimating 12,250 as 12,000 and the percent of copyright lawyers as 75% results in 0.75 × 12,000, or approximately 9,000. The question stem says the 4,250 of these lawyers are female: 9,000 – 4,250 = 4,950, or approximately (B) 5,000.

  20. E

    To calculate the total number of lawyers between 51 and 60 add the number of males to the number of females. The number of males is approximately the same number above 200,000 that the number of females is below 200,000, so 200,000 + 200,000 = 400,000 is a good approximation for the number of lawyers between 51 and 60. Of those 400,000 lawyers, the pie chart shows 11% were in tax law, which means the correct answer must be more than 400,000 × 0.1 = 40,000. (E) is correct because it is the only choice that is more than 40,000.